目录

贝塞尔曲面

曲面细分

Loop细分（Loop Subdivision）

Catmull-Clark 细分（Catmull-Clark Subdivision）

曲面简化

---

贝塞尔曲面

然后前面讲了贝塞尔曲线，这里讲一下这个贝塞尔曲面

那怎么样从贝塞尔曲线到贝塞尔曲面的转换呢，前面我们说到这个逐段的贝塞尔曲线是通过四个控制点来画的，这里贝塞尔曲面是通过16个控制点来画的

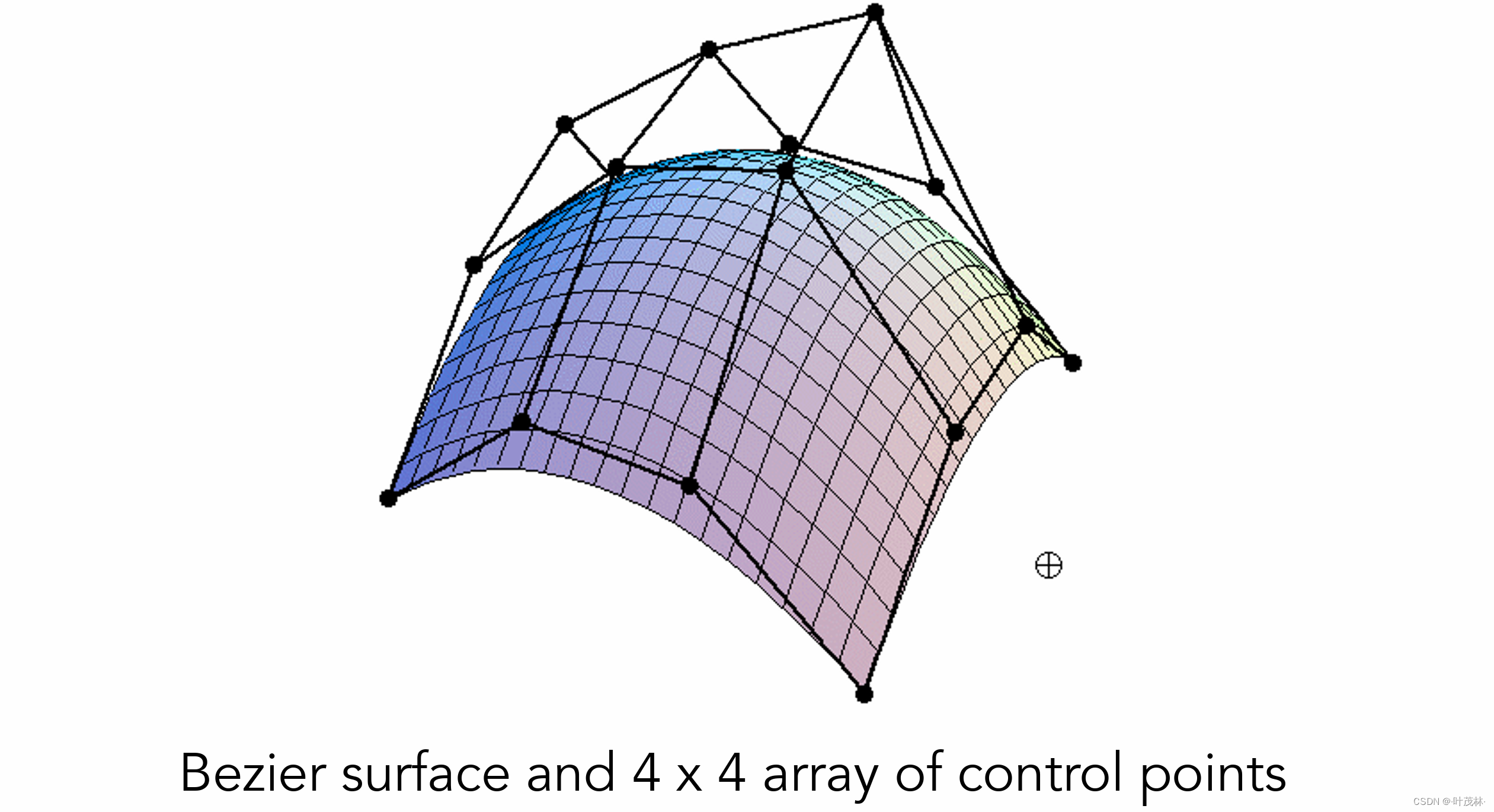
把这16个控制点排列成4×4网格，那么每行或者每列是不是有四个控制点就可以画出一条贝塞尔曲线，这样就可以画出四条并列的贝塞尔曲线，然后比分说有这样一个平面从另一个方向上扫过去，是不是会和这四条线有四个交点，那这四个点是不是又可以画出一条贝塞尔曲线，这样是不是就可以用贝塞尔曲线布满整个曲面

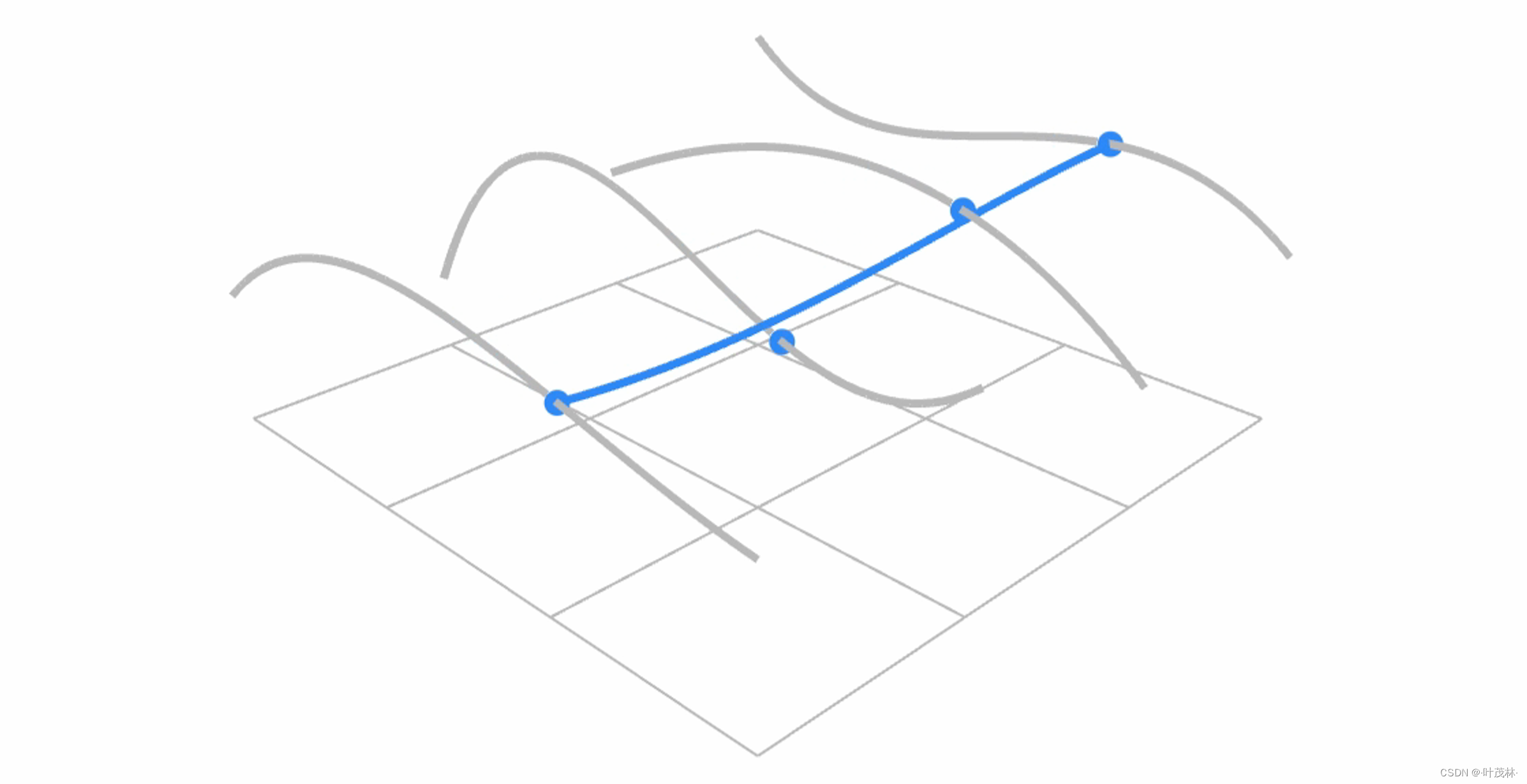
具体来说，在时间u时可以确定四条贝塞尔曲线上的四个点对不对，然后在时间u上的时间v是不是可以通过u的四个控制点确定的贝塞尔曲线v时刻的点，这样通过（u，v）就可以确定曲面上任意一点的位置，这个贝塞尔曲面就可以画出来了

曲面细分

我们可以通过将组成物体的多边形继续细分成更多的多边形来使这个物体产生更多的细节或者表面更加光滑

Loop细分（Loop Subdivision）

这个loop细分是针对三角形的，而且这个loop是个人名，和循环没关系

loop细分就分两步，第一步将一个三角形拆分成多个三角形，第二步移动这些新生成的三角形

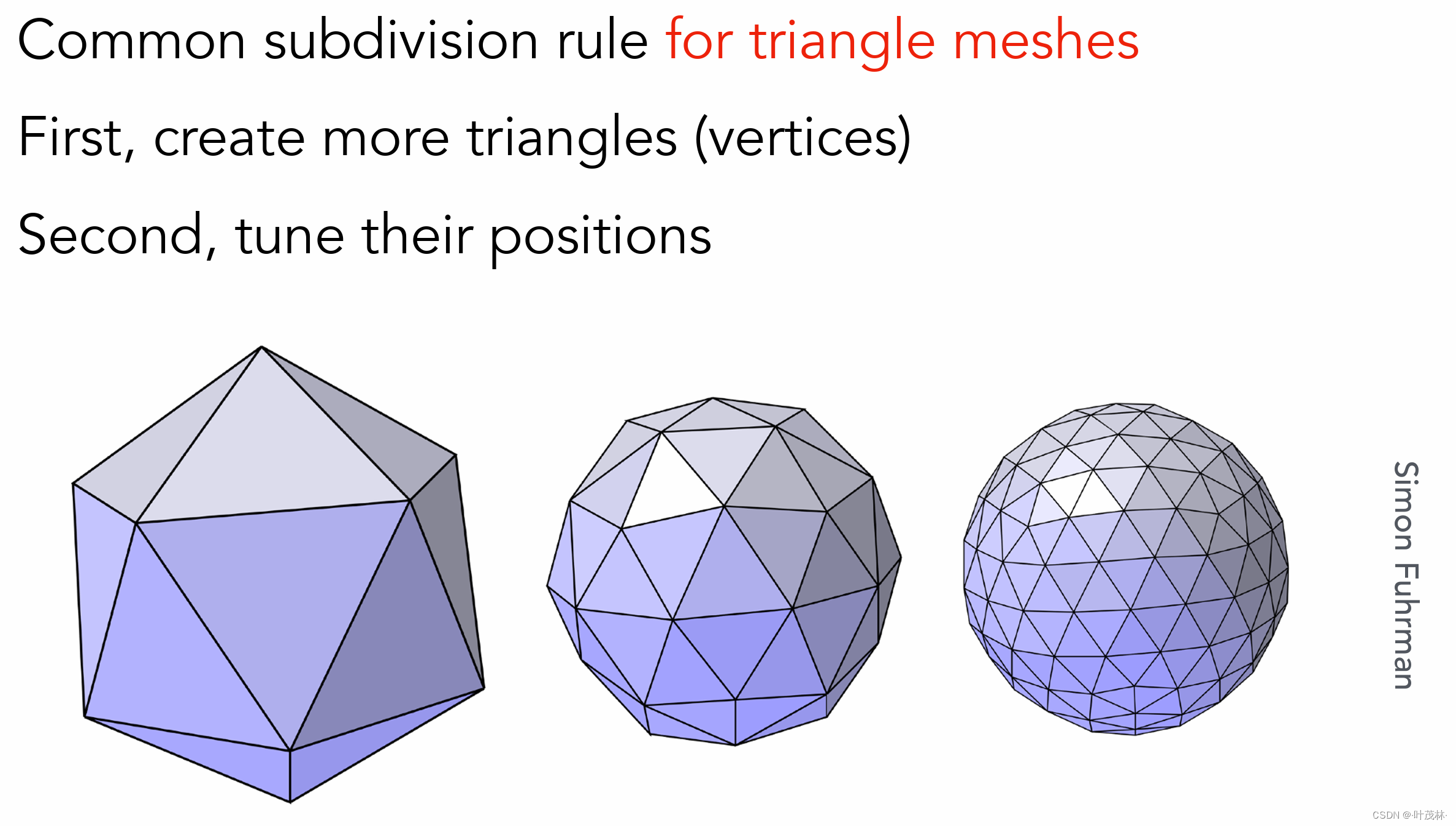
具体怎么做呢？第一步拆分三角形好做，直接连接各条边上的中点，这样一下子就可以一个变多个小三角形

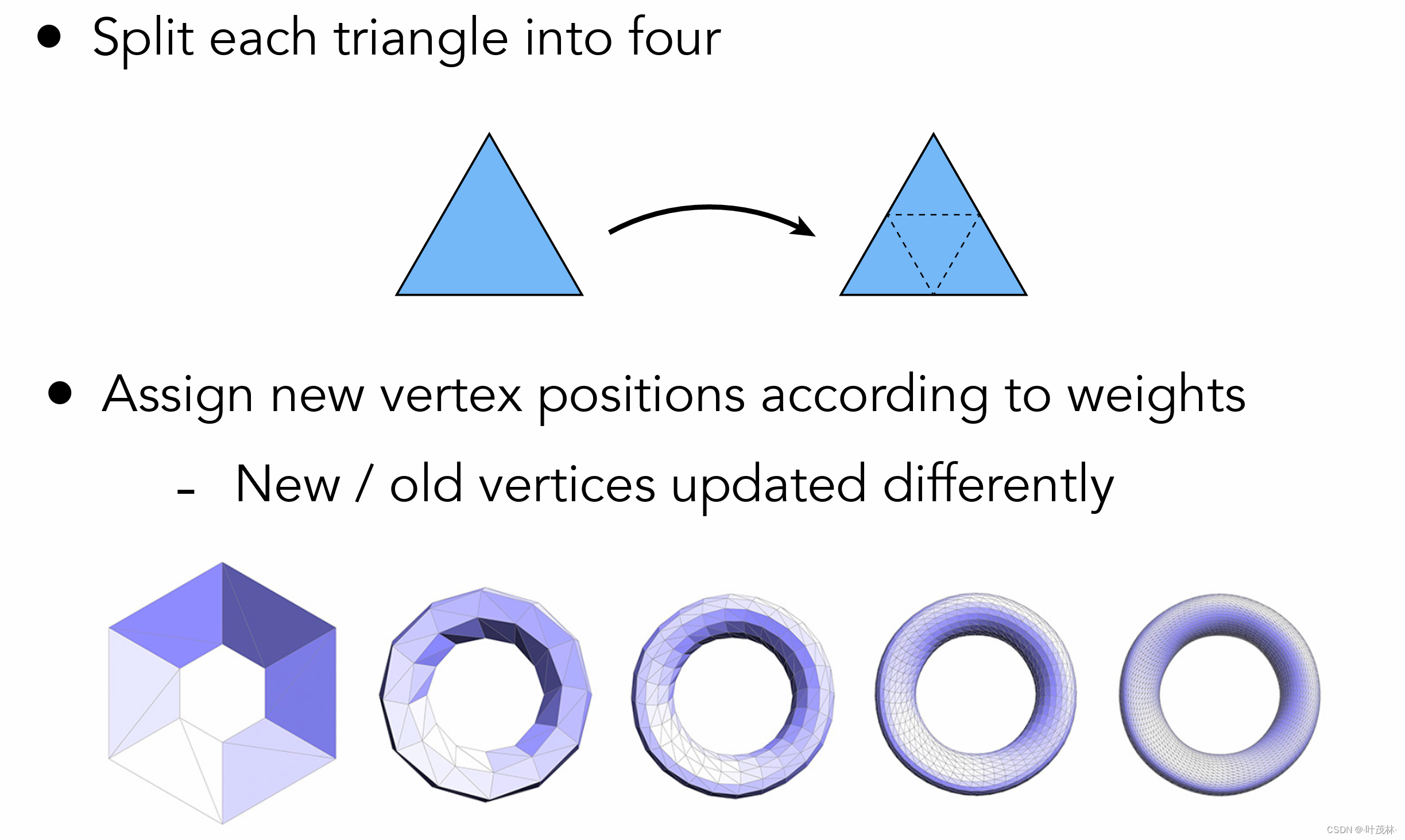
问题在于如何移动这些新的三角形的位置对吧，其实就是如何移动这些三角形的顶点问题，我们把顶点分成两种，一种是旧顶点，就是原本三角形的三个顶点，另一种是新形成的顶点，就是原来三角形三条边上的中点，这两种顶点需要分开处理

对于新生成的顶点，那这个点它肯定在一条三角形边上，那一条边会有两个三角形共享，那就可以找出这四个顶点ABCD，中间的白点就是我们要移动的点，这个白点的位置就是周围这四个顶点的加权平均值，我们认为它和AB更接近一些，因此AB权值更大

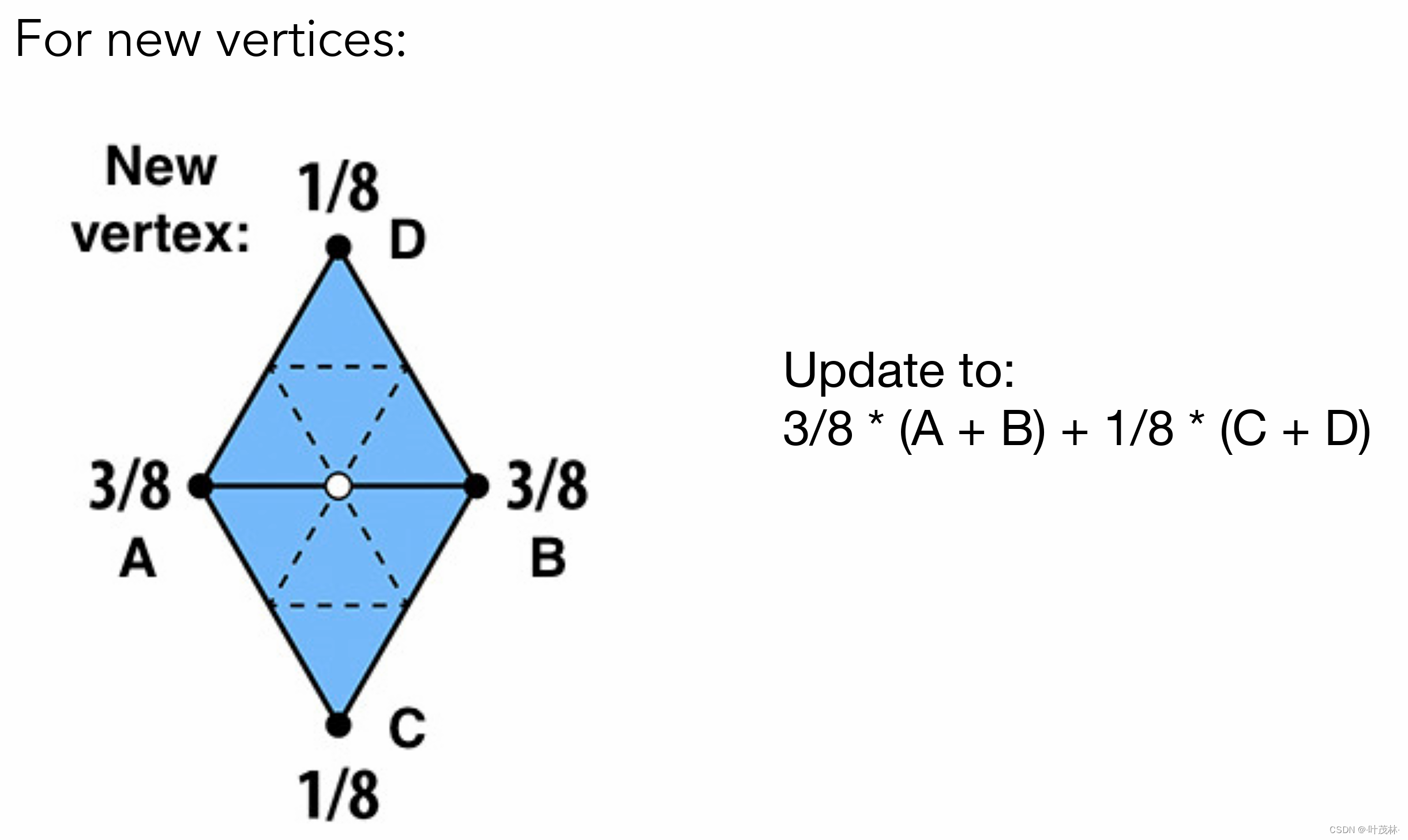
对于旧顶点，它肯定会是多个三角形的顶点是不是，我们定义两个值n和u，这个n就是这个旧顶点的度，所谓顶点的度是指它连接了多少条边，这个u呢，如果n=3那么u=3/16，否则u=3/(8n)，好，同样是周围这些顶点以及它本身的一个加权平均，对于自己的权值是1-nu，对于周围顶点的平均值的权值是u

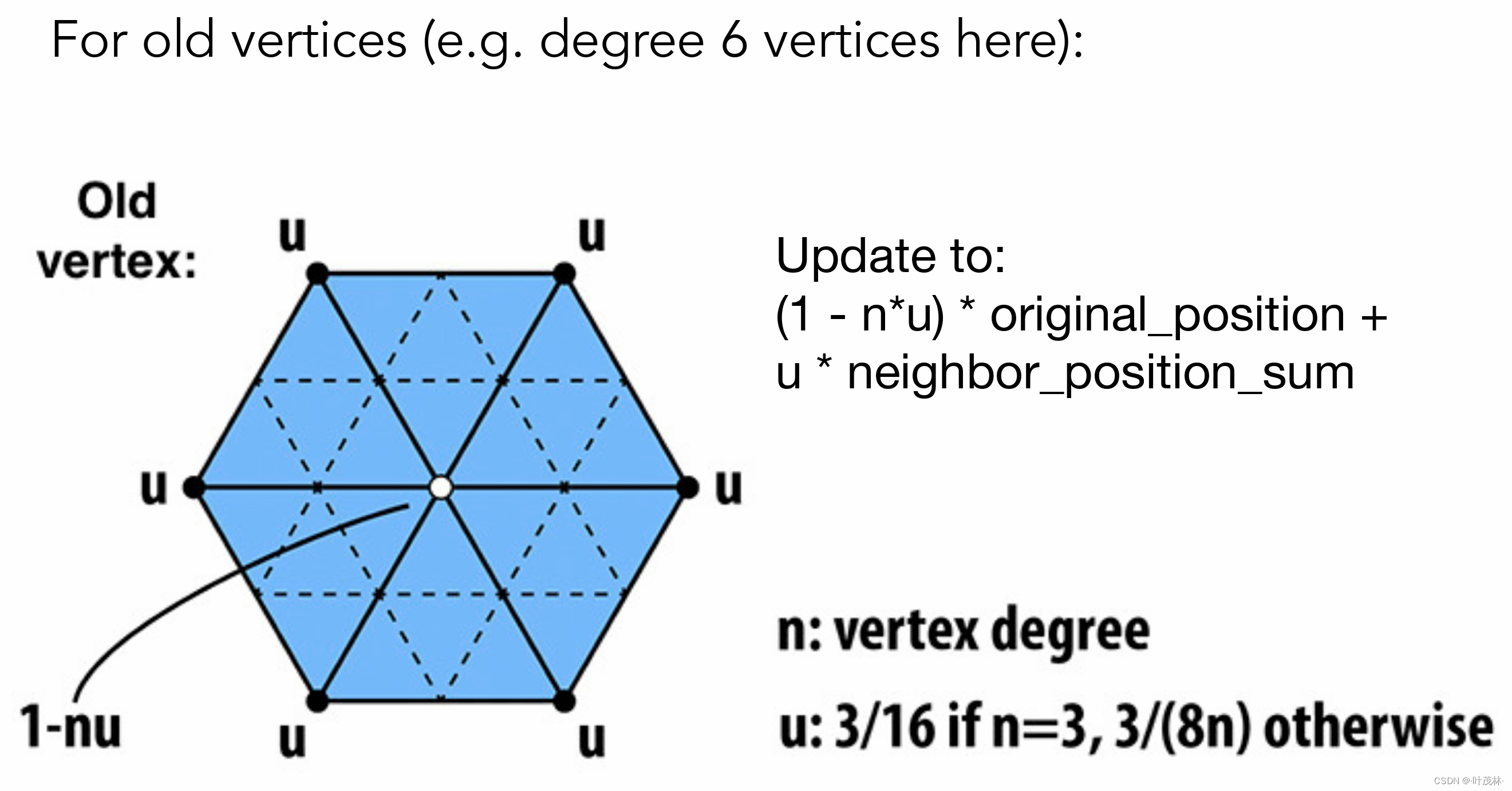
这样我们先拆分三角形，然后移动三角形的顶点就可以实现这个loop细分

Catmull-Clark 细分（Catmull-Clark Subdivision）

然后我们的loop细分其实可以知道它只能用于三角形对不对，那对于这个普通网格多边形怎么办呢，这就是Catmull-Clark 细分做的事情

对于这么些多边形我们定义这个不是四边形的叫非四边形，然后顶点的度（就是连接的边数）不是4的顶点叫作奇异点，就像下面这个图有两个非四边形，有两个奇异点

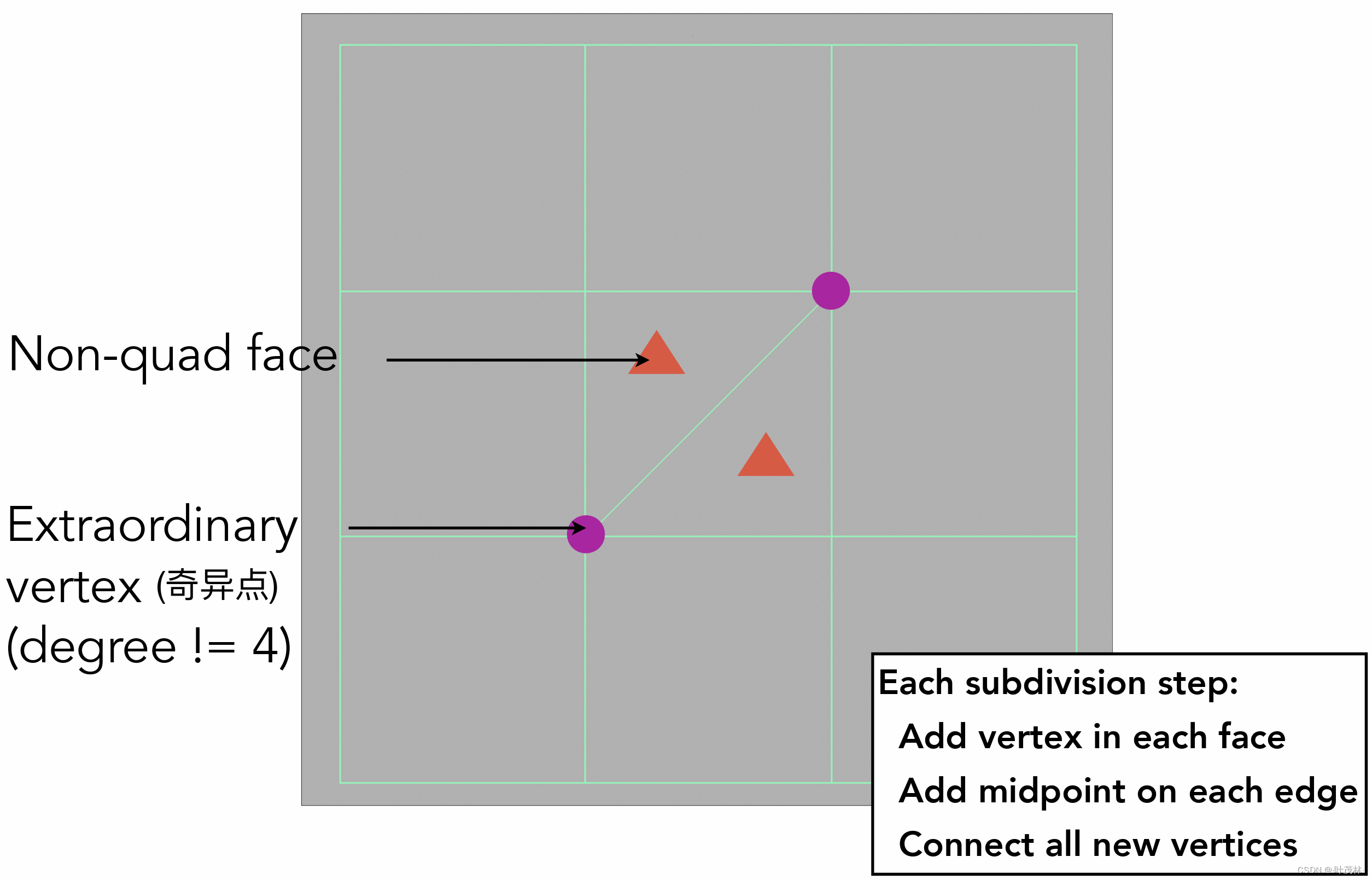
然后对于这些多边形，我们给每个面添加上一个顶点，先不管它放哪，然后每条边取中点，连接所有顶点，然后就会变成这样，可以发现这样操作之后呢，非四边形就会消失，取而代之的是多了奇异点，而且消失的非四边形数等于增加的奇异点数

我们就通过这种方式来细分这个曲面

然后我们需要解决的问题就是如何移动新增加的这些点的位置 

依然我们将顶点分成几类处理，对于这个在面上增加的点f，它的值就是周围四个顶点的平均值，然后对于边的中点，它的值是上下两个顶点再加上两边f点的平均值

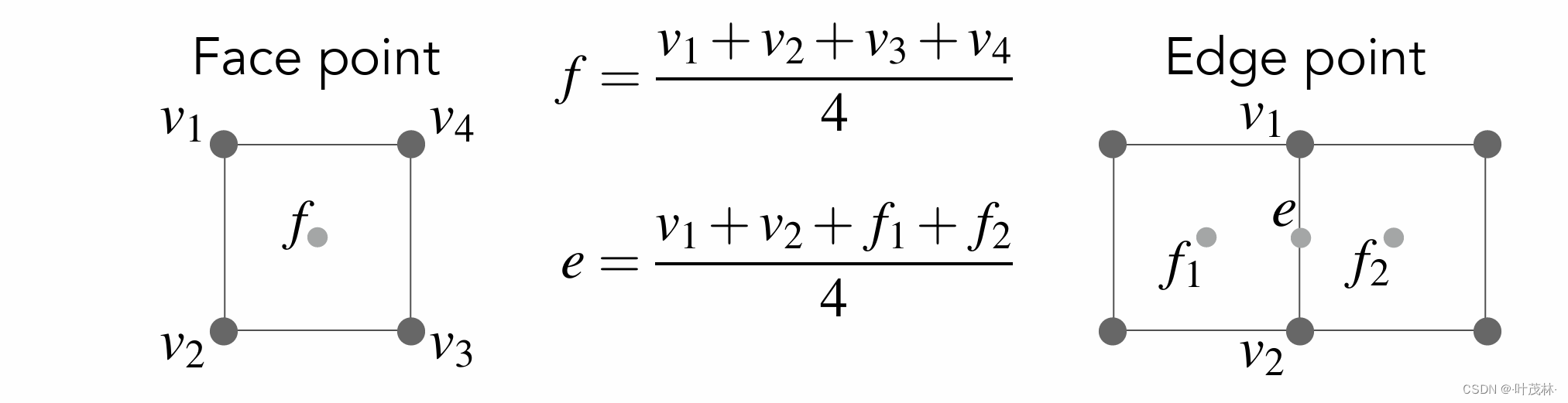
还有就是原来的旧顶点，是通过这样的加权平均计算

这样就可以实现这个Catmull-Clark 细分

曲面简化

我们可以通过减少使用的多边形数量来近似的表示原来的物体

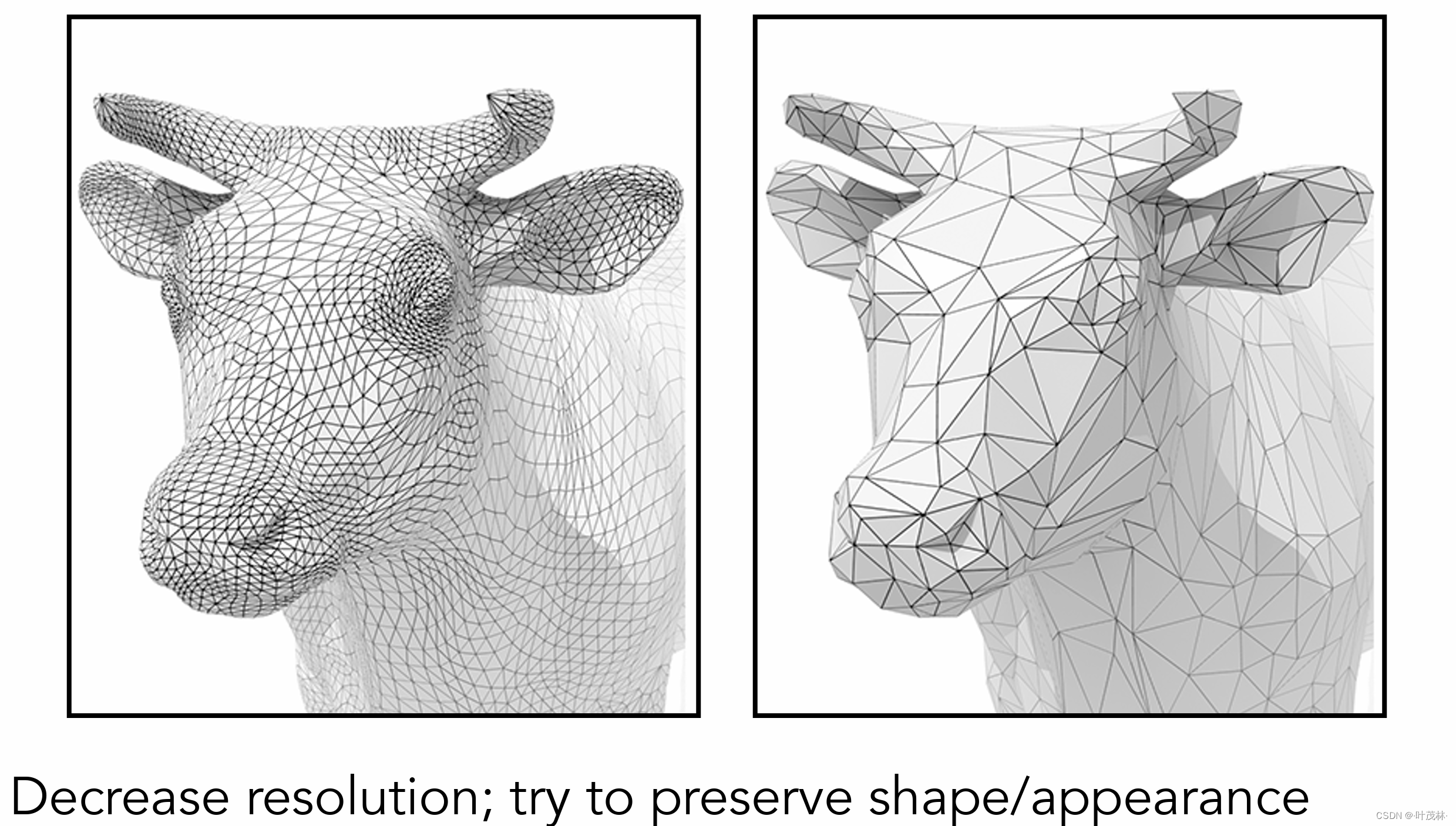
因为很多时候我们不需要知道这个物体的细节，或者说我从很远的地方看它，本就无需细节

怎么实现这种简化呢，是通过边坍缩的方式实现的，所谓边坍缩，指的是，将某条边的两个顶点融合，这样这条边就消失了

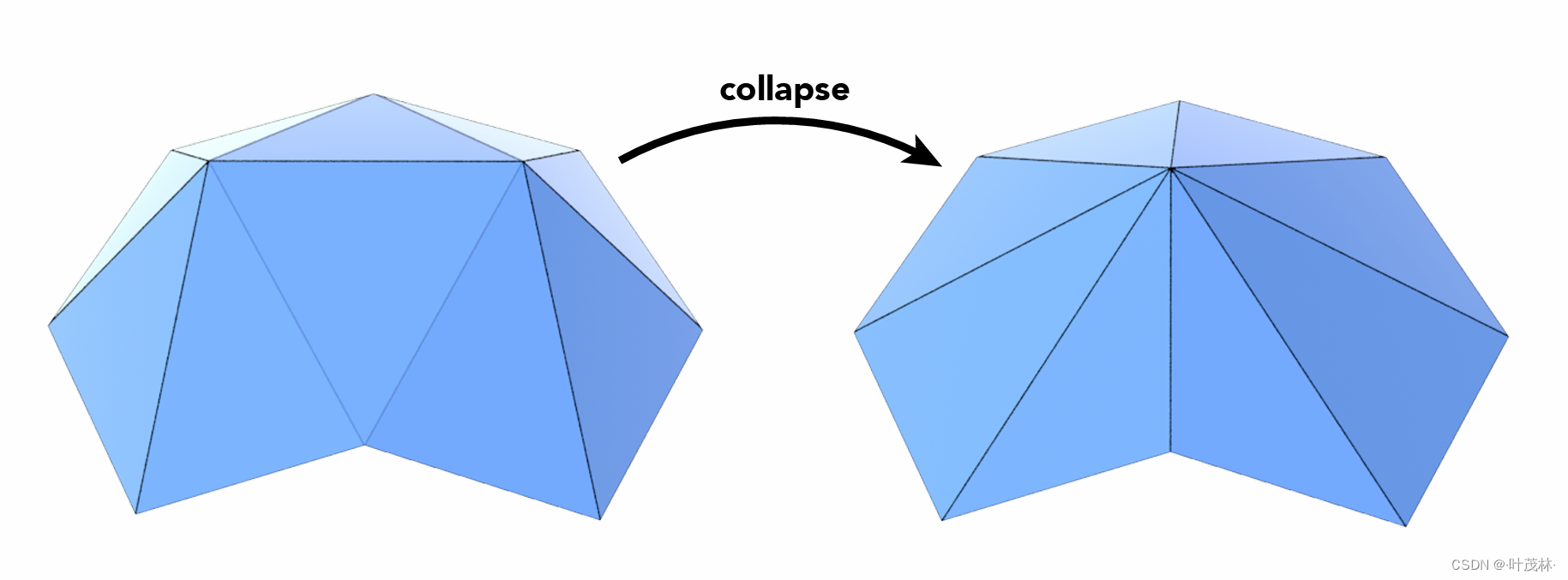这样的问题在于，我如何去挑选哪些边来消失呢，即哪些边是价值比较小的需要消失

这里是通过这个叫二次误差度量的衡量方式来比较的，对于一条边坍缩后我去计算融合后的顶点和周围顶点的距离的平方和，我去选取这个距离平方和最小的来进行坍缩

这里的距离平方和使用了堆进行存储