Fisher线性判别分析
原理
LDA(Linear Discriminant Analysis)是一种经典的线性判别方法,又称Fisher判别分析。该方法思想比较简单:给定训练集样例,设法将样例投影到一维的直线上,使得同类样例的投影点尽可能接近和密集,异类投影点尽可能远离。
Fisher线性判别分析主要包括两个目标:
-
最大化类间方差(Maximize Between-Class Variance): 通过找到一个投影方向,使得不同类别的样本在投影后的均值之间的距离最大。这确保了不同类别在投影空间中有明显的差异。
-
最小化类内方差(Minimize Within-Class Variance): 在类间方差最大的同时,还要保证每个类别内部的样本在投影后尽量聚集在一起,即类内方差最小。
通过这两个目标,Fisher线性判别分析产生了一个投影方向,可以将原始数据映射到一个低维空间,同时保留类别之间的差异。这个投影方向通常可以用一个权重向量(投影向量)表示。
在实际应用中,Fisher线性判别分析经常用于模式识别、人脸识别、图像处理等领域,特别是在处理具有多个类别的分类问题时,它可以提供较好的分类性能。与主成分分析(PCA)不同,Fisher线性判别分析是有监督的降维方法,因为它利用了类别信息来优化投影方向。
Python代码
详见注释
import numpy as np
import matplotlib.pyplot as plt# 读取数据,并根据类别分类
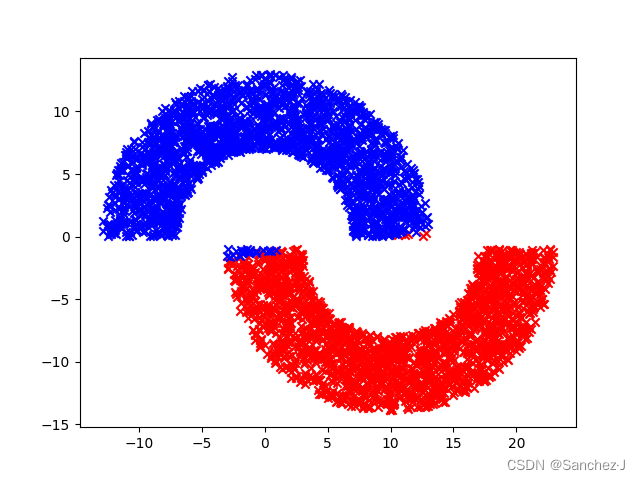
def readdata(filename):fr = open(filename)numberOfLines = len(fr.readlines()) # 获取数据行数data = np.zeros((numberOfLines, 2))label = []fr = open(filename)index = 0# 该函数readdata以文件名作为输入,并从文件中读取数据。# 它初始化一个数组data以存储数据点,以及一个列表label以存储相应的标签。for line in fr.readlines():line = line.strip()listFromLine = line.split()data[index, 0] = float(listFromLine[0])data[index, 1] = float(listFromLine[1])label.append(float(listFromLine[-1]))index += 1# 遍历文件中的每一行。使用strip()去除行首和行尾的空格,# 使用split()将行分割成一个值列表,然后将前两个值转换为浮点数,存储在data数组中。# 最后一个值也被转换为浮点数并附加到label列表中。# 分类index1 = np.array([index for (index, value) in enumerate(label) if value == -1.0])index2 = np.array([index for (index, value) in enumerate(label) if value == 1.0])data0 = data[index1]data1 = data[index2]# 在读取所有数据点之后,它通过基于标签筛选data来创建两个数组data0和data1。# data0包含标签为-1.0的点,# data1包含标签为1.0的点。return data0, data1def calculatesi(datai, ui):si = np.zeros((datai.shape[1], datai.shape[1]))# 这一行创建了一个形状为(datai.shape[1], datai.shape[1])的零矩阵,# 并将其赋给变量si。这个矩阵将用于存储协方差矩阵。for xi in datai:# 这一行开始一个循环,遍历datai中的每个数据点,将每个数据点表示为xi。m = xi - ui# 这一行计算了数据点xi与均值向量ui之间的差异,将结果存储在变量m中。si += m * m.reshape(2, 1)# 这一行更新协方差矩阵si。它将矩阵m与其转置相乘,并将结果累加到si上。# m.reshape(2, 1)是为了确保矩阵乘法的维度匹配。return sidef fish(data0, data1):# 计算两数据集data0和data1的均值向量u0和u1,# 通过np.mean函数计算每个特征的平均值。u0 = np.mean(data0, axis=0)u1 = np.mean(data1, axis=0)# 计算类内离散度矩阵si# 调用calculatesi函数,该函数用于计算协方差矩阵。# 分别对data0和data1使用均值向量u0和u1计算了类内离散度矩阵si。s0 = calculatesi(data0, u0)s1 = calculatesi(data1, u1)# 总类内离散度矩阵# 这一行计算了总的类内离散度矩阵sw,# 将两个类内离散度矩阵s0和s1相加。sw = s0 + s1# 求逆# 使用np.linalg.inv函数计算总类内离散度矩阵sw的逆矩阵,sw_inv = np.linalg.inv(sw)# 计算投影w# 将总类内离散度矩阵的逆矩阵sw_inv与均值向量差异(u0 - u1)相乘得到。w = np.dot(sw_inv, (u0 - u1))w0 = (np.dot(w.T, u0) + np.dot(w.T, u0)) / 2return w, u0, u1def judge(filename, w, u0, u1):# 读取数据# 打开文件filename,获取文件行数,# 初始化一个大小为(numberOfLines, 2)的零数组test_data,以及一个空列表label。# 接着,通过循环读取文件的每一行,将每行的数据提取出来,转换为浮点数,并存储到test_data数组中。fr = open(filename)numberOfLines = len(fr.readlines()) # 获取数据行数test_data = np.zeros((numberOfLines, 2))label = []fr = open(filename)index = 0for line in fr.readlines():line = line.strip()listFromLine = line.split()test_data[index, 0] = float(listFromLine[0])test_data[index, 1] = float(listFromLine[1])index += 1# 判断类别# 计算投影后的数据点在投影向量w上的位置,并根据其与两个类的中心的距离来判断类别。# 如果点到类别0的中心的距离小于点到类别1的中心的距离,则将类别标签设为-1.0,否则设为1.0。center_0 = np.dot(w.T, u0)center_1 = np.dot(w.T, u1)for s in test_data:y = np.dot(w.T, s)if abs(y - center_0) < abs(y - center_1):label.append(-1.0)else:label.append(1.0)# 分类# 根据类别标签将数据点分成两个数组test_data0和test_data1,# 分别包含属于类别-1.0和1.0的数据点,并将它们作为函数的返回值。index1 = np.array([index for (index, value) in enumerate(label) if value == -1.0])index2 = np.array([index for (index, value) in enumerate(label) if value == 1.0])test_data0 = test_data[index1]test_data1 = test_data[index2]return test_data0, test_data1def draw(data0, data1, w):plt.scatter(data0[:, 0], data0[:, 1], c='red', marker='x')plt.scatter(data1[:, 0], data1[:, 1], c='blue', marker='x')plt.show()if __name__ == '__main__':# 读取数据集并根据数据类别分类data0, data1 = readdata("train_data.txt")# 计算最佳投影ww, u0, u1 = fish(data0, data1)# 判断测试集test_data0, test_data1 = judge("test_data.txt", w, u0, u1)# 绘图draw(test_data0, test_data1, w)
结果: