1.并查集的定义
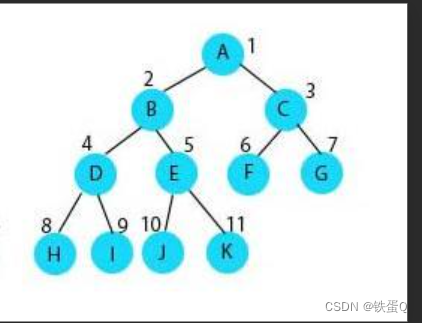
并查集其实也是一种树形结构，在使用中通常用森林的方式来表示
并查集的逻辑结构其实就是集合
并查集一般可以通过双亲写法（顺序结构）来完成，即通过一个数组存储父亲结点的下标
int s[10005];
int main()
{for(int i=1; i<=n; i++){s[i]=-1;
//为什么一开始都归属于-1呢，我们要从定义入手，我们的数组存储的是父亲结点的下标，若从-1开始，
//可以意味着，他们一开始都是单独的元素，方便后续的查和并操作}
}2.并查集能进行的操作
1.查：寻找一个元素归属于哪个集合或者说判断两个元素是否同属于一 个集合
int cha(int x)
{while(s[x]>=0)//当指针不为-1时就会一直向前搜索，直到搜索出根结点x=s[x];return x;//返回根结点的下标
}
2.并：将两个子树并在一起，通常是将小子树并在大子树上面
void bing(int root1,int root2)
{if(root1==root2) return;//传进来两个根节点一样的本来就是本身，不用合并，直接返回就好s[root2]=root1;//将子树2的指针指向子树1的下标
}
3.并查集相关例题
第一题：并查集
题解，这题也是十分简单，合并操作就是用上述的并，判断是否在一个集合就要用查了，如果相等，则证明在一个集合里
看AC代码：
#include<bits/stdc++.h>
using namespace std;
int n,m;int a[20005];//定义一个双亲写法的数
int z,x,y;
int cha(int x)//查
{while(a[x]>=0){x=a[x];}return x;
}
void bing(int root1,int root2)//并
{if(root1==root2)return;a[root2]=root1;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){a[i]=-1;}for(int i=0;i<m;i++){scanf("%d%d%d",&z,&x,&y);if(z==1){bing(cha(x),cha(y));//合并树的时候合并的是根}if(z==2){int p=cha(x);int q=cha(y);if(p==q)printf("Y\n");elseprintf("N\n");}}return 0;
}
第二题：亲戚
题解：这题也是很简单，判断是否是亲戚，只需要判断是否在一个结点就可以，因此上面那题差不多
AC代码：
#include<bits/stdc++.h>
using namespace std;
int n,m,p;
int s[10005];
int x,y;
int cha(int x)
{while(s[x]>=0)x=s[x];return x;
}
void bing(int root1,int root2)
{if(root1==root2) return;s[root2]=root1;
}
int main()
{scanf("%d%d%d",&n,&m,&p);for(int i=0; i<m; i++)// for(int i=1; i<=n; i++){s[i]=-1;}{scanf("%d%d",&x,&y);bing(cha(x),cha(y));}int r,t;for(int i=0; i<p; i++){scanf("%d%d",&r,&t);int te=cha(r);int re=cha(t);if(te==re)printf("Yes\n");elseprintf("No\n");}return 0;
}
第三题：朋友
题解，我们只需要放置两个数组，判断那边的子树的节点更少就可以
AC代码
#include<bits/stdc++.h>
using namespace std;
int n,m,p,q;
int x,y,z,t;
int a[10005];
int b[10005];int cha(int x,int s[])
{while(s[x]>=0)x=s[x];return x;
}
void bing(int root1,int root2,int z[])//唯一要处理的就是尽量往小明和小红身上连接子树
{if(root1==root2)return ;if(root1==1){z[root2]=root1;}else if(root2==1){z[root1]=root2;}else{z[root2]=root1;}
}
int main()
{scanf("%d%d%d%d",&n,&m,&p,&q);for(int i=1; i<=n; i++){a[i]=-1;}for(int i=1; i<=m; i++){b[i]=-1;}for(int i=0; i<p; i++){scanf("%d%d",&x,&y);bing(cha(x,a),cha(y,a),a);}for(int i=0; i<q; i++){scanf("%d%d",&z,&t);bing(cha(-z,b),cha(-t,b),b);}int sum1=0,sum2=0;for(int i=1; i<=n; i++){if(cha(i,a)==1)sum1++;}for(int i=1; i<=m; i++){if(cha(i,b)==1){sum2++;}}printf("%d\n",min(sum1,sum2));return 0;
}
