目录
力扣1863.找出所有子集的异或总和再求和
力扣47.全排列II编辑
力扣17.电话号码的字母组合电话号码的字母组合https://leetcode.cn/problems/letter-combinations-of-a-phone-number/编辑
力扣22.括号生成
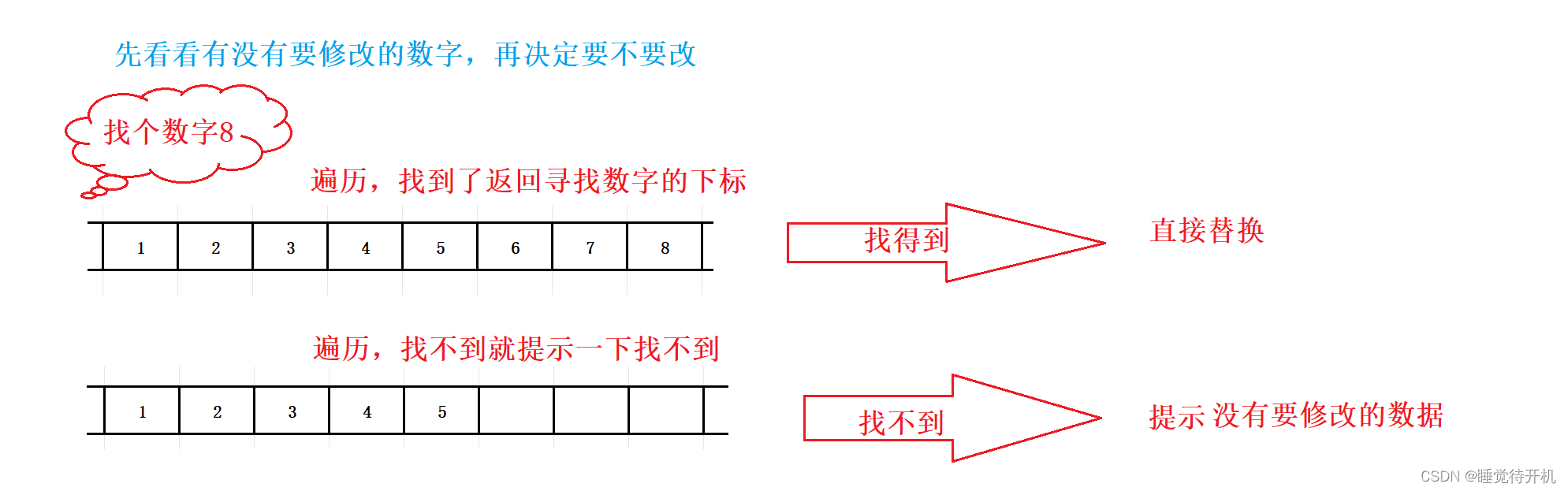
力扣1863.找出所有子集的异或总和再求和


class Solution {int sum;int path;//表示当前路径的返回值public int subsetXORSum(int[] nums) {dfs(nums,0);return sum;}public void dfs(int[] nums,int pos){sum+=path;for(int i=pos;i<nums.length;i++){//m添加当前数字path^=nums[i];dfs(nums,i+1);//此处,要想他回溯是什么时候回溯,是dfs走完了回溯,它会先走到下面,然后回到上一层,那么当他会到上一层时,是回溯什么,回溯到上一层的上一层,换句话说,那她就要把当前的值去除path^=nums[i];}}
}我觉得对我这种代码能力不是很强的人来说,有几个重要的点
1.掌握各个集合的使用,2.了解内部的一些数学知识,3.了解算法的使用,我觉得这三个都很重要。
所以在这里介绍一个知识:
异或的消消乐:假如说1异或2,得出来的结果假如再异或一个2就会变回1,这也就是两个一样的还原成原先数字,这就是我们的消消乐原理。
力扣47.全排列II
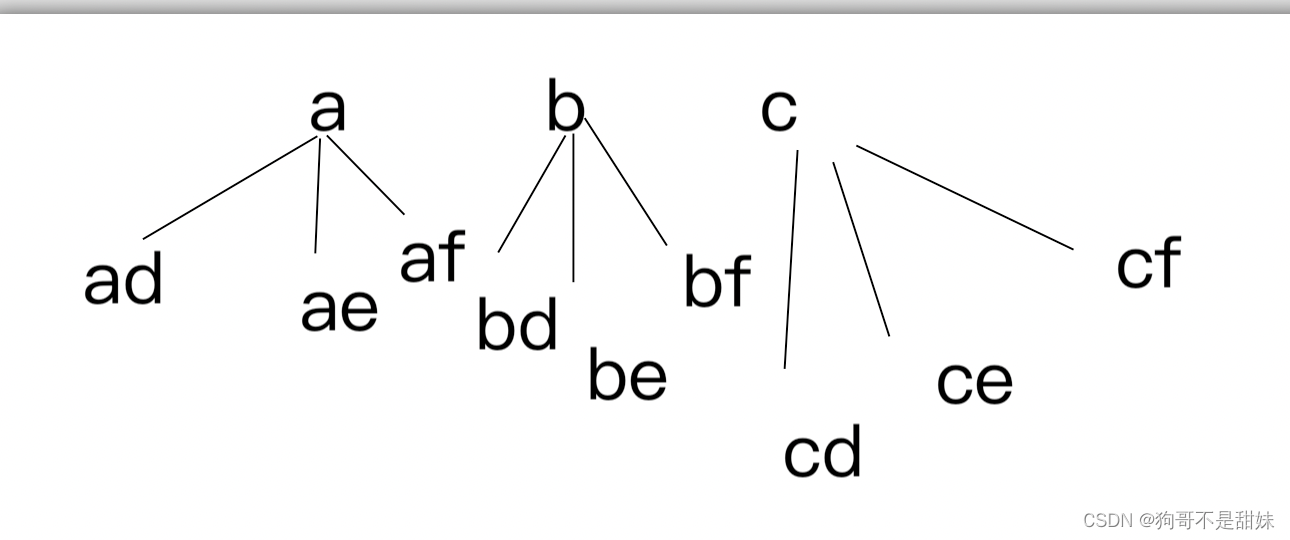
讲实话,刚开始我还不会写,对全排列不是很理解,虽然前一个做了这个问题但还是生疏,到现在,真正自己去动手画一个决策树,真的就能把想要的写出来。
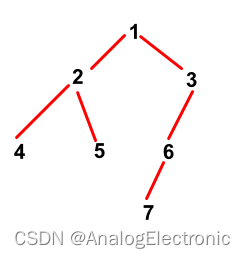
这个是全排列I的时候的决策树

这个全排列II和全排列I的区别,就是测设用例要求返回不重复的全排列
全排列的情况II,从合法的角度去写,如果他是第一个,可以无脑进入遍历,因为他不用考虑重复,如果他不是第一个,那么就不能有重复的,假如有重复的那么他的前一个一定是true(上一层遍历过的)否则不会成功
class Solution {List<List<Integer>>ret=new ArrayList<>();List<Integer>path=new ArrayList<>();boolean []check;public List<List<Integer>> permuteUnique(int[] nums) {check=new boolean[nums.length];Arrays.sort(nums);dfs(nums);return ret;}public void dfs(int[]nums){if(path.size()==nums.length){ret.add(new ArrayList<>(path));}for(int i=0;i<nums.length;i++){//我们去重的时候想去nums[i]==nums[i+1],万一有可能他们两个重复的不在一起呢。//所以我们要进行排序//||从左往右执行的,假如左边不成立,那么右边必定成立的情况 true的潜台词是nums[i]==nums[i-1]//i==0的原因是,他是第一个元素,我们可以大胆去使用它。if(check[i]==false&&(i==0||nums[i]!=nums[i-1]||check[i-1]==true)){path.add(nums[i]);check[i]=true;dfs(nums);path.remove(path.size()-1);check[i]=false;}}} }假如说我们考虑不合法的情况
当他出现不合法的情况,就要跳过,那么什么是不合法的情况呢
当他已经是true的时候,不合法,或者出现了相同的值并且他的前一个值是false的情况,那么就是这一层出现了两个相同的数,所以会有错误
class Solution {List<List<Integer>>ret=new ArrayList<>();List<Integer>path=new ArrayList<>();boolean []check;public List<List<Integer>> permuteUnique(int[] nums) {check=new boolean[nums.length];Arrays.sort(nums);dfs(nums);return ret;}public void dfs(int[]nums){if(path.size()==nums.length){ret.add(new ArrayList<>(path));}for(int i=0;i<nums.length;i++){//我们去重的时候想去nums[i]==nums[i+1],万一有可能他们两个重复的不在一起呢。//所以我们要进行排序//||从左往右执行的,假如左边不成立,那么右边必定成立的情况 true的潜台词是nums[i]==nums[i-1]//i==0的原因是,他是第一个元素,我们可以大胆去使用它。if(check[i]==true||(i!=0&&nums[i]==nums[i-1]&&check[i-1]!=true)){continue;}path.add(nums[i]);check[i]=true;dfs(nums);path.remove(path.size()-1);check[i]=false;}} }
力扣17.电话号码的字母组合
电话号码的字母组合 https://leetcode.cn/problems/letter-combinations-of-a-phone-number/
https://leetcode.cn/problems/letter-combinations-of-a-phone-number/
首先映射关系是我们需要考虑的,怎么处理映射关系呢?
搞一个字符串数组即可-
2:abc 3:def。。。前两个可以空着(因为0,1没有值)
我们需要使用StringBufer path,我们要给他更改字符的时候,假如是String更改值不方便。所以我们使用StringBuffer
回溯:删除掉之前增加的那个字符
递归出口:
、class Solution {String[] hash={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};List<String>ret=new ArrayList<>();StringBuffer path=new StringBuffer();public List<String> letterCombinations(String digits) {if(digits.length()==0){return ret;}dfs(digits,0);return ret;} public void dfs(String digits,int pos){//为什么是等于pos,因为pos代表的是这个字符串有多长,够了就说明可以回溯了if(digits.length()==pos){ret.add(path.toString());return; } //把cur数组存储hash里面的字符串,pos的变化相当于是切换字符串 ,abc先a然后到达def的d String cur=hash[digits.charAt(pos)-'0']; //一次遍历cur里面的数组,然后path路径再次加入路径元素 for(int i=0;i<cur.length();i++){//i是表示假如说号码2,是说号码2的第几个,不是总体的长度path.append(cur.charAt(i));dfs(digits,pos+1);path.deleteCharAt(path.length()-1); }} }
力扣22.括号生成
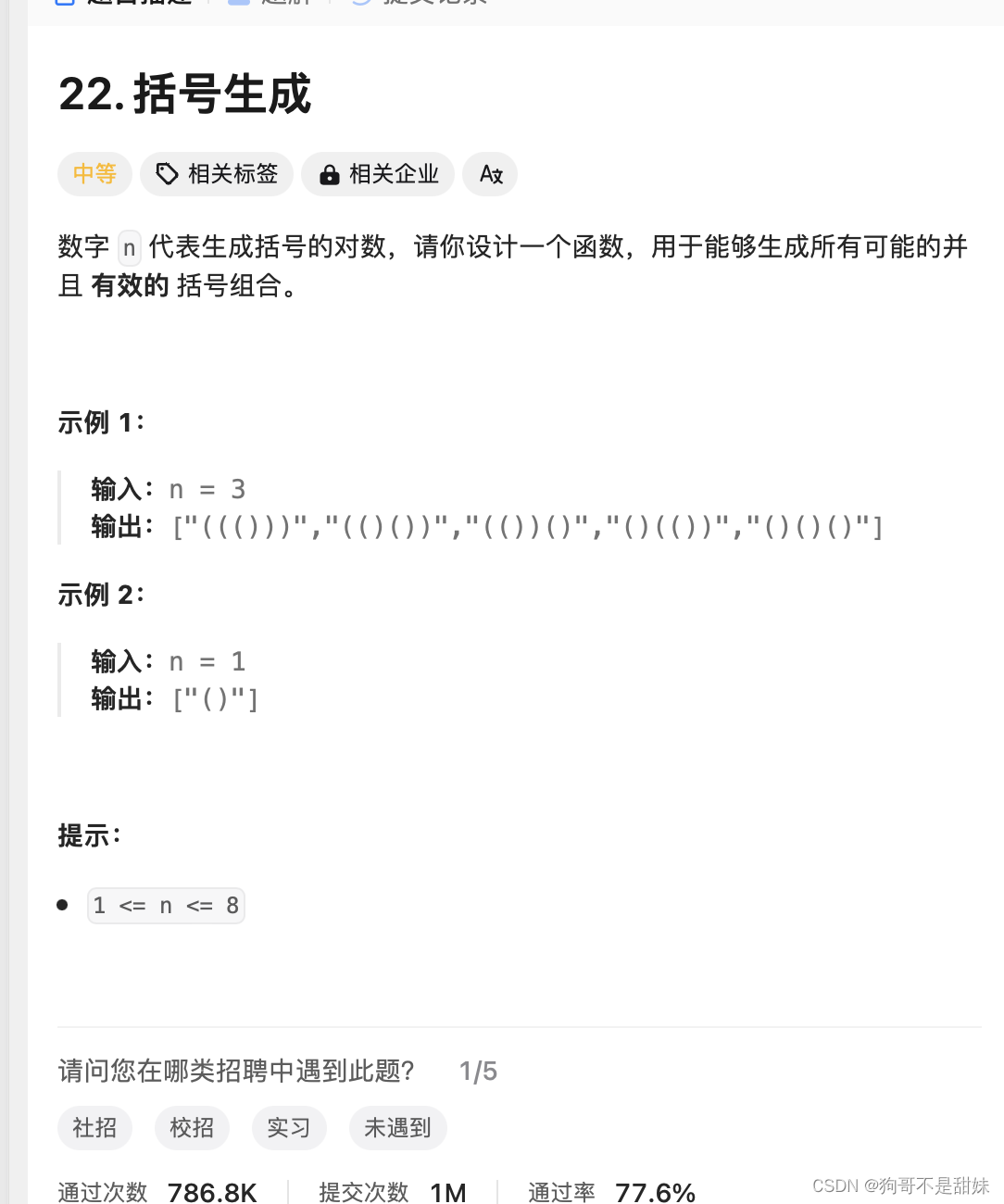
要先思考,什么是有效的括号组合,必须要同时满足这两个条件,才能满足有效的括号
首先左括号数量等于右括号的数量
从头开始的任意一个字串,左括号数量>=右括号数量
n=x,n是几对的意思. 也就是说明有2x个括号
1.全局变量
左括号数量,右括号数量,(k一共多少对)
path记录路径,ret
dfs(一个参数即可)
回溯:当向上走的的时候,干掉path最后一个即可
当right==n,我们就可以返回了
class Solution {int left;int k;int right;List<String> ret=new ArrayList<>();StringBuffer path=new StringBuffer(); public List<String> generateParenthesis(int n) {k=n;dfs();return ret;} public void dfs(){if(right==k){ret.add(path.toString());return;} 假如left<括号的对数,那么我们就可以添加左括号 //在这里其实我有一个思考,什么时候+右括号呢,这不是一直都会进入左括号吗。if(left<k){path.append("(");left++;dfs();path.deleteCharAt(path.length()-1);left--; } //假如left>right就可以一直+右括号if(left>right){path.append(")");right++;dfs();path.deleteCharAt(path.length()-1);right--; }} }假如left<括号的对数,那么我们就可以添加左括号
在这里其实我有一个思考,什么时候+右括号呢,这不是一直都会进入左括号吗。这也引起我的思考,后来也就一瞬间通透了,他是一直向下走,而不是横着走,这也就是深度搜索,然后回溯(走完一条路)之后向右走,(( ),假如是这样如果他就会回溯后,加入进去右括号