文章目录
- 一、300、最长递增子序列
- 二、674、最长连续递增序列
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、300、最长递增子序列
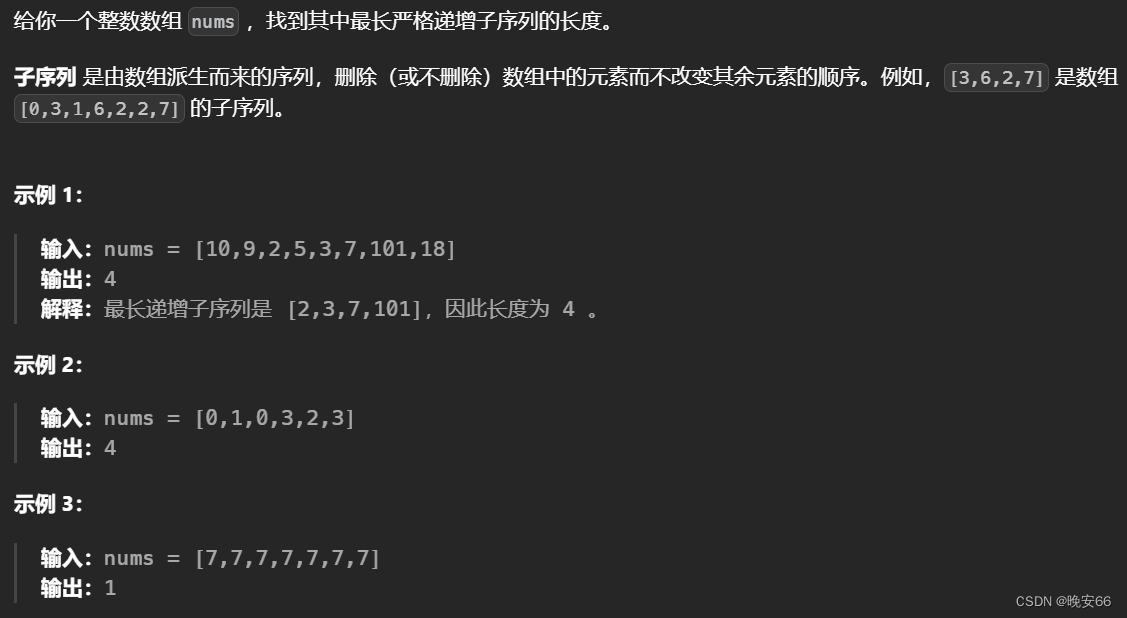
思路分析:
- 第一步,动态数组的含义。 d p [ i ] dp[i] dp[i]代表 i i i之前包括以 i i i结尾的最长递增子序列的长度。我们在做递增比较的时候,两个子序列分别以 n u m s [ i ] nums[i] nums[i]和 n u m s [ j ] nums[j] nums[j]作为结尾。
- 第二步,递推公式。位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
- 第三步,元素初始化。dp数组中的所有元素至少为1,因此都初始化为1。
- 第四步,递归顺序。一共有两层循环,外层循环遍历整个nums数组,里层循环遍历 [ 0 , i − 1 ] [0,i-1] [0,i−1]的nums数组。如果当前的nums[i]>nums[j]那么我们取 [ 0 , i − 1 ] [0,i-1] [0,i−1]中最大的长度作为 d p [ i ] dp[i] dp[i]的值。
- 第五步,打印结果。 d p [ n u m s . s i z e ( ) − 1 ] dp[nums.size()-1] dp[nums.size()−1]未必是最大的,因此需要筛选出最大的结果返回。
if (dp[i] > result) result = dp[i];
程序如下:
// 300、最长递增子序列
class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int result = 1;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}if (dp[i] > result) result = dp[i];}return result;}
};
复杂度分析:
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( n ) O(n) O(n)。
二、674、最长连续递增序列
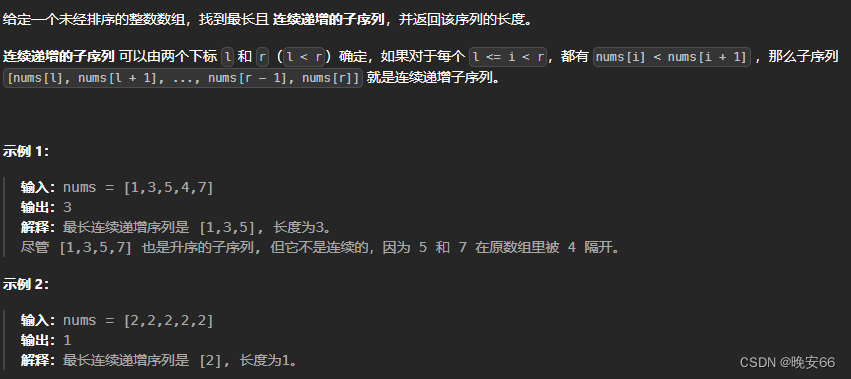
思路分析:本题和300、LeetCode最长递增子序列类似,区别在于最长子序列从非连续到连续。因为要求连续的递增子序列,那么我们只需要考察连续这个性质,而连续递增只需要对比nums数组中相邻的两个数。
- 第一步,动态数组的含义。 d p [ i ] dp[i] dp[i]代表 i i i之前包括以 i i i结尾的最长递增子序列的长度。我们在做递增比较的时候,两个子序列分别以 n u m s [ i ] nums[i] nums[i]和 n u m s [ i − 1 ] nums[i-1] nums[i−1]作为结尾。
- 第二步,递推公式。本题只要一个循环,如果 n u m s [ i ] nums[i] nums[i] 大于 n u m s [ i − 1 ] nums[i-1] nums[i−1],那么dp[i] = dp[i - 1] + 1。
if (nums[i] > nums[i-1]) dp[i] = dp[i - 1] + 1;
- 第三步,元素初始化。dp数组中的所有元素至少为1,因此都初始化为1。
- 第四步,递归顺序。循环从 i = 1 i=1 i=1开始。
- 第五步,打印结果。 d p [ n u m s . s i z e ( ) − 1 ] dp[nums.size()-1] dp[nums.size()−1]未必是最大的,因此需要筛选出最大的结果返回。
if (dp[i] > result) result = dp[i];
程序如下:
// 674、最长连续递增序列
class Solution2 {
public:int findLengthOfLCIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int result = 1;for (int i = 1; i < nums.size(); i++) {if (nums[i] > nums[i-1]) dp[i] = dp[i - 1] + 1;if (dp[i] > result) result = dp[i];}return result;}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( n ) O(n) O(n)。
三、完整代码
# include <iostream>
# include <vector>
using namespace std;// 300、最长递增子序列
class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int result = 1;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}if (dp[i] > result) result = dp[i];}return result;}
};// 674、最长连续递增序列
class Solution2 {
public:int findLengthOfLCIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int result = 1;for (int i = 1; i < nums.size(); i++) {if (nums[i] > nums[i-1]) dp[i] = dp[i - 1] + 1;if (dp[i] > result) result = dp[i];}return result;}
};int main() {vector<int> nums = { 1,3,5,4,7 };Solution2 s1;int result = s1.findLengthOfLCIS(nums);cout << result << endl;system("pause");return 0;
}
end