15. 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
**注意:**答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
思路
-
容器可能包含多个键相同的键-值对,因此需要找到与指定,键对应的所有值。为此,可使用 multimap::count( )确定有多少个值与指定的键对应,再对迭代器递增, 以访问这些相邻的值
-
map 和 multimap 之间的区别在于,后者能够存储重复的键,而前者只能存储唯一的键。只针对键,与值无关
-
本题使用哈希法过于复杂,所以使用双指针法。
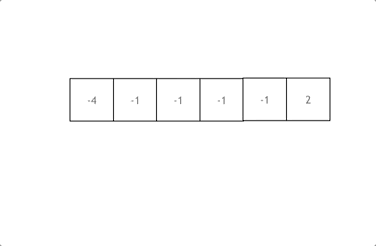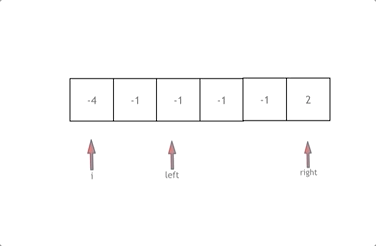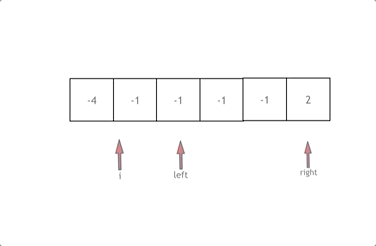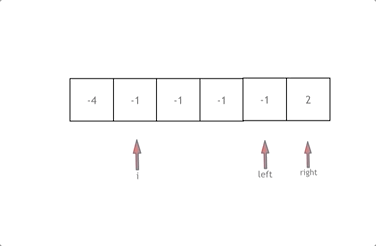
- 首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
- 依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
- 如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
- 如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
代码
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(), nums.end());int left;int right;int count = nums.size() - 1;vector<vector<int>> result;// result.reserve(count>255? 256:0);result.reserve(1024);// 预留出空间,减少拷贝int i = 0;while (i < count && nums[i] <= 0) {if (i > 0 && nums[i] == nums[i - 1]) {i++;continue;//如果当前元素和上一个元素相同,那么就结束这次循环}left = i + 1;right = nums.size() - 1;// left不能超过rightwhile (left < right) {if (nums[i] + nums[left] + nums[right] > 0) {right--;// 如果sum>0,那么right左移,减少sum} else if (nums[i] + nums[left] + nums[right] < 0) {left++;// 如果sum<0,那么left右移,增加sum} else {vector<int> temp{nums[i], nums[left], nums[right]};result.push_back(temp);// 如果sum=0,则当left++时,sum>0,那么right--;反之也成立left++;right--;while (nums[left] == nums[left - 1] && left < right) {left++;// 防止出现[-2,0,0,2,2]的情况}while (nums[right] == nums[right + 1] && left < right) {right--;}}}i++;}return result;}
};