算法练习-左叶子之和（思路+流程图+代码）-编程知识

难度参考

难度：中等

分类：二叉树

难度与分类由我所参与的培训课程提供，但需要注意的是，难度与分类仅供参考。且所在课程未提供测试平台，故实现代码主要为自行测试的那种，以下内容均为个人笔记，旨在督促自己认真学习。

题目

        计算给定二叉树的所有左叶子之和。
        示例1:
        输入：root=[3,9,20,null,nu,15,7]
        输出：24
        解释：在这个二叉树中，有两个左叶子，分别是9和15，所以返回24

        示例2:
        输入：root=[1]
        输出：0

思路

计算给定二叉树的所有左叶子之和的问题的思路主要是通过递归遍历一颗二叉树的所有节点，并且识别哪些节点是左叶子节点（即，一个节点没有子节点并且是其父节点的左子节点）。以下是解决该问题的具体思路：

确认基本情况：如果当前节点为空，那么它不会对左叶子之和作任何贡献，返回0。
检查当前节点是否为左叶子节点，即它是不是其父节点的左子节点且没有子节点。如果是，将它的值加到左叶子之和上。
对于每个非空节点，递归检查它的左子节点和右子节点：
- 对左子节点调用递归函数，同时将当前节点作为父节点传递。
- 对右子节点也调用递归函数，并同样将当前节点作为父节点传递。
从左右子树接收到的左叶子之和需要合计到当前总和中。
递归过程持续进行，直到所有节点被访问。
一旦所有节点被递归遍历完毕，可以得到所有左叶子节点之和。
最后，返回这个总和值给调用的地方，通常是在主函数中对这个递归函数的初始调用。

示例

假设有一棵这样的二叉树：

        3/ \9  20/  \15   7

在这颗树中，节点 9 和节点 15 是左叶子节点。

首先注意，左节点是不是根节点，并且是其父节点的左子节点，且没有左子树和右子树的节点。

程序从 main 函数调用 sumOfLeftLeaves 函数开始执行，并传入二叉树的根节点 root（节点值为3）。
sumOfLeftLeaves 函数首先检查传入的节点不为空。这个检查用于结束递归调用。
因为我们从根节点（节点 3）开始，它没有父节点，所以不会被当作左叶子。
我们首先递归进入根节点的左子节点（节点 9）。在这一步中，传入的父节点是根节点（节点 3）。
在调用 sumOfLeftLeaves(root->left, root) 时，函数检测到节点 9 没有子节点，并且它是其父节点（节点 3）的左子节点，因此节点 9 被认为是一个左叶子，其值被加入到和中。
递归继续从节点 9 的左子节点和右子节点（两者均为空）调用 sumOfLeftLeaves，但是这些调用立即返回 0，不会对总和产生影响。
接下来，从根节点（节点 3）的递归调用进入其右子节点（节点 20），此时函数需要检查节点 20 的左右子节点。
当递归调用 sumOfLeftLeaves(root->right->left, root->right)（节点 15）时，它会发现节点 15 没有子节点，并且是其父节点（节点 20）的左子节点。于是节点 15 的值也被加入到和中。
当 sumOfLeftLeaves 递归调用节点 20 的右子节点（节点 7），这会导致最终返回 0，因为它不满足左叶子的条件。
随着递归调用的完成，每个节点对总和的贡献（如果它是左叶子节点）会被累加起来。
最终，所有的调用完成后，回到 main 函数中打印出了所有左叶子之和。

所以，在上面的二叉树示例中，左叶子节点是节点 9 和节点 15，它们的值分别是 9 和 15，所以 sumOfLeftLeaves(root) 将会返回 9 + 15 = 24，这个值会在 main 函数中被打印出来。

梳理

这样实现的原因在于算法正确地定义了何为左叶子节点，并且逐步遍历了二叉树的每个节点去判断是否符合左叶子节点的定义。算法的关键步骤在于：

左叶子的定义：
- 必须是一个叶子节点，意即没有子节点。
- 必须是它父节点的左子节点。
递归的使用：
- 算法通过递归的方式遍历树中的所有节点。
- 对于每个节点，递归函数会先判断该节点是否是左叶子节点。
- 如果是，它会加上该节点的值到总和中。
- 接着，算法会递归地调用当前节点的左右子节点，并传递当前节点作为新调用的父节点。
- 递归的终止条件是当访问到的节点为 NULL，即没有子节点时。
累积求和：
- 在遍历树的同时，将碰到的所有符合条件的左叶子节点的值累加起来。
- 每次对节点调用递归函数时，将返回的和（对左右子树递归调用的结果）累积到当前和中。

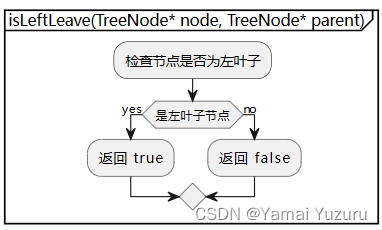
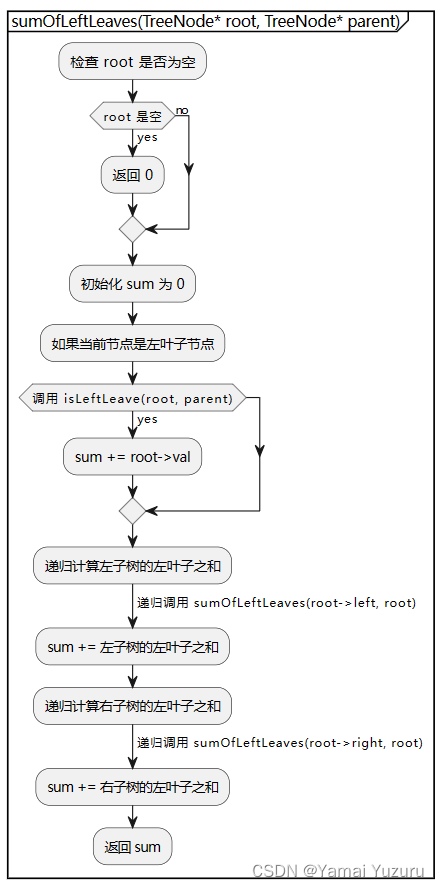
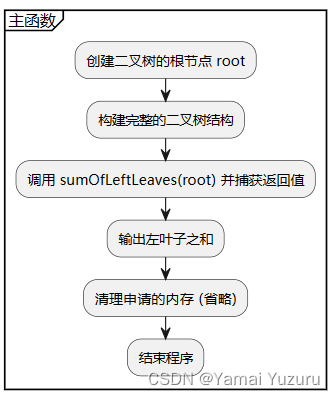
递归其实不适合用流程图表示，但目前不会别的方法。

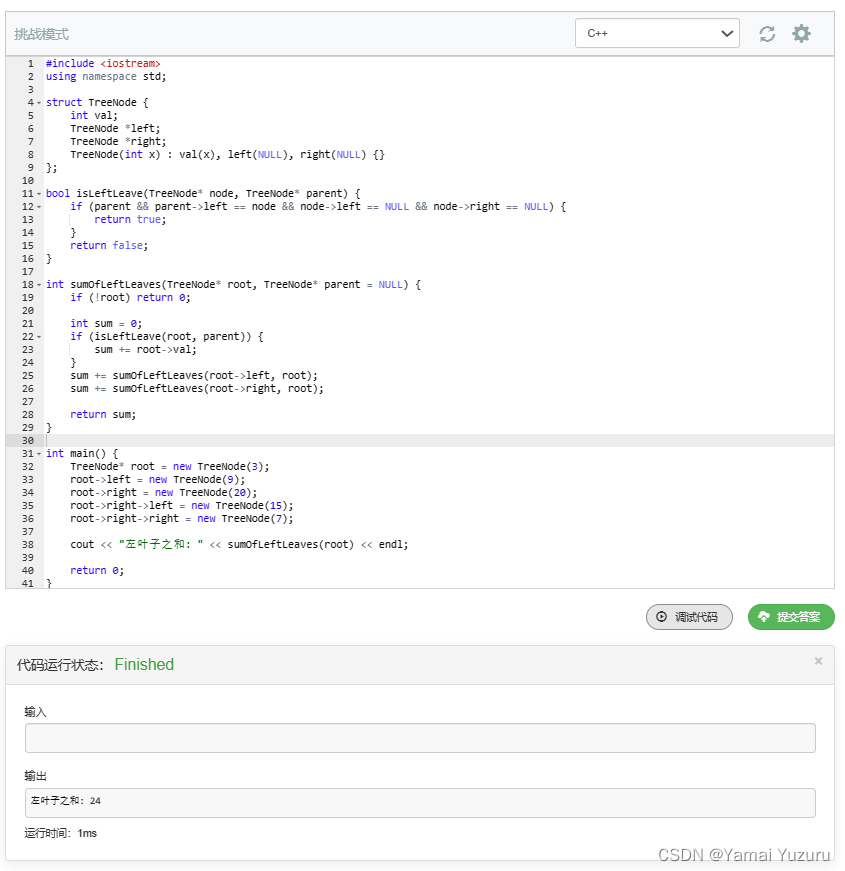
代码

#include <iostream>
using namespace std;// 定义二叉树节点的结构体
struct TreeNode {int val;                // 节点内的值TreeNode *left;         // 指向左子树的指针TreeNode *right;        // 指向右子树的指针TreeNode(int x) : val(x), left(NULL), right(NULL) {} // 初始化结构体的构造函数
};// 辅助函数，判断一个节点是否是左叶子节点
bool isLeftLeave(TreeNode* node, TreeNode* parent) {// 如果节点不是根节点，并且是其父节点的左子节点，且没有左子树和右子树，则为左叶子节点if (parent && parent->left == node && node->left == NULL && node->right == NULL) {return true;}return false;
}// 计算所有左叶子之和的递归函数
int sumOfLeftLeaves(TreeNode* root, TreeNode* parent = NULL) {if (!root) return 0; // 如果节点为空，则返回0int sum = 0; // 初始化左叶子之和为0if (isLeftLeave(root, parent)) { // 如果当前节点是左叶子节点，则将其值加到sum上sum += root->val;}sum += sumOfLeftLeaves(root->left, root); // 递归计算左子树的左叶子之和sum += sumOfLeftLeaves(root->right, root); // 递归计算右子树的左叶子之和return sum; // 返回计算的左叶子之和
}// 主函数
int main() {// 根据提供的例子手动创建二叉树，以下代码根据示例1构建二叉树TreeNode* root = new TreeNode(3);root->left = new TreeNode(9); // 左叶子节点root->right = new TreeNode(20);root->right->left = new TreeNode(15); // 左叶子节点root->right->right = new TreeNode(7);// 计算左叶子之和并输出cout << "Sum of left leaves: " << sumOfLeftLeaves(root) << endl;// 清理申请的内存 (这部分代码省略，实际使用时需注意内存释放)return 0; // 程序结束
}