今天我们来讲一下树上的搜索知识。

1.树上搜索

树上搜索，我们之前学习了一种特殊的结构，树！

我们之前研究了图上的搜索，我们之前还学了树这种特殊的图，接下来我们就来研究一下在树上的搜索。

如果想要遍历整棵树，可以和图一样，从一个点开始（一般从根开始），每次找一个没有访问过的点访问就可以了。

但是树总有它的特殊性，那就是从根开始搜索，到达每个点的时候一定只有它的父节点是之前访问过的，所以我们并不必使用vis数组记录每个点有没有被访问过，只需要记录每个点的父节点是哪个节点，这样看这个点连着的节点时，就只需要判断它不是这个点的父节点就可以往下搜索了。

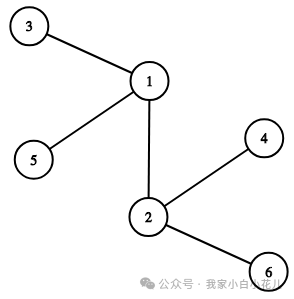
比如这样一个图，如果 1 是根，那访问到 
2 的时候一定可以走 
4 和 6 ，只是不能走 
1 ，那就走 
4 和 6 就可以了。

记录父节点可以使用一个数组，不过如果之后我们不会再关心每个点的父节点是谁，只是在这次搜索才用，那就可以直接把父节点当作参数传进来。

这样搜索代码写下来就是这样

void dfs(int u, int fa) { // fa 就是父节点cout << u << endl;for (int i = 0; i < G[u].size(); i++) {int v = G[u][i];if (v != fa) {dfs(v, u); // 那往下搜索，到 v 的时候父节点就是我们目前在的节点 u}}
}

调用dfs从根搜索的时候传给fa的参数常常是这个根本身或者一个不存在的点 0。

平常输入树的方式有很多，比如明确说明每个点的父节点，或者明确说明了一个点是另一个点的父节点，此时，我们只需要父节点向子节点连有向边就足够了，对于根节点，有可能会明确知道，如果不知道，那可以统计每个点是不是有父节点或者统计每个点的度数来找到根节点，此时fa这个参数也可以就不用了。

例如下面是一些输入数据，共 
4 行，每行两个整数 u, v示 u 是 
v 的父节点。

#include <iostream>
#include <vector>
using namespace std;
vector <int> G[105];
void dfs(int u, int fa) {cout << u << endl;for (int i = 0; i < G[u].size(); i++) {int v = G[u][i];if (v != fa) {dfs (v, u);}}
}
int main() {int n;cin >> n;for (int i = 1; i < n; i++) {int u, v;cin >> u >> v;G[u].push_back(v);G[v].push_back(u);}dfs (1, 0);return 0;
}