450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
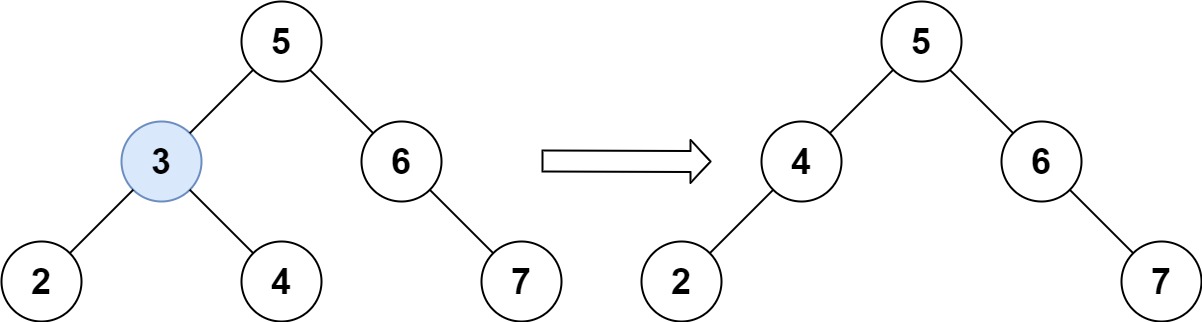
输入:root = [5,3,6,2,4,null,7], key = 3 输出:[5,4,6,2,null,null,7] 解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0 输出: []
思路:要是被删除的节点是叶子节点或者只有左孩子或右孩子,那么处理起来很简单。要是需要被删除的节点既有左孩子又有右孩子,就需要左进一步处理了。那么,在找到需要删除的节点后,需要把被删除节点的左子树接在被删除节点的右子树的最左叶子节点,因此,用一个节点遍历找到右子树的最左叶子节点,接上左子树。接下来,需要做的就是删除被删除节点了,root=root->right(下面代码中的delete都是可以缺省的,只是一个释放内存的操作)。
代码实现:
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if(!root) return root;if(root->val == key) {if(!root->left && !root->right) {delete root;return nullptr;}else if(!root->left) {auto ret = root->right;delete root;return ret;}else if(!root->right) {auto ret = root->left;delete root;return ret;}else {TreeNode *node = root->right;while(node->left) {node = node->left;}node->left = root->left;auto r = root;root = root->right;delete r;return root;}}if(root->val > key) root->left = deleteNode(root->left, key);if(root->val < key) root->right = deleteNode(root->right, key);return root;}
};669. 修剪二叉搜索树
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。 可以证明,存在 唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
示例 1:

输入:root = [1,0,2], low = 1, high = 2 输出:[1,null,2]
示例 2:
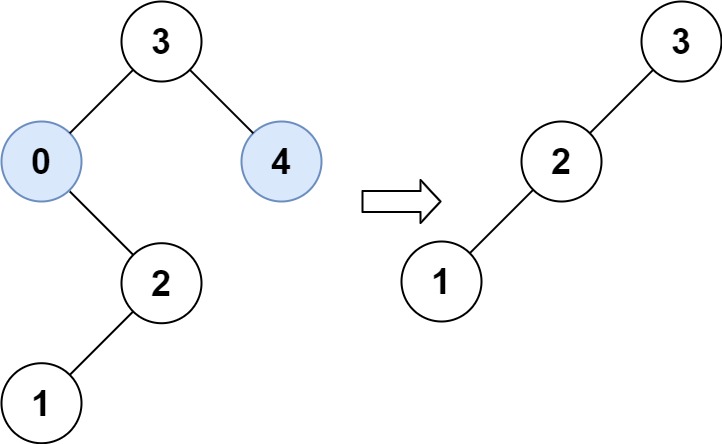
输入:root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出:[3,2,null,1]
思路:也是递归调用,首先是当走到空节点返回,针对于该被修剪的节点,在满足被剪条件后,断开这个连接(度),连接到左孩子或右孩子即可(具体看是大于范围->找左孩子,小于范围->找右孩子)。
代码实现:
class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if(root == nullptr) return nullptr;if(root->val > high) {TreeNode *left = trimBST(root->left, low, high);return left;}if(root->val < low) {TreeNode *right = trimBST(root->right, low, high);return right;}root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:

输入:nums = [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

示例 2:
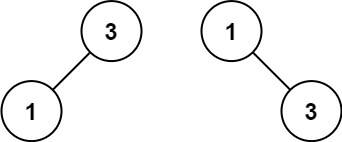
输入:nums = [1,3] 输出:[3,1] 解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
思路1:迭代,使用三个队列,一个维护节点,另外两个维护下标(因为要建立高度平衡的二叉搜索树,那么就需要left,mid,right三个下标)
代码实现1:
class Solution {
public:TreeNode* sortedArrayToBST(vector<int>& nums) {queue<TreeNode *>que;queue<int>rightQue;queue<int>leftQue;TreeNode *root = new TreeNode(0);que.push(root);leftQue.push(0);rightQue.push(nums.size() - 1);while(!que.empty()) {TreeNode *node = que.front();que.pop();int left = leftQue.front();leftQue.pop();int right = rightQue.front();rightQue.pop();int mid = left + ((right - left)/2);node->val = nums[mid];if(left <= mid - 1) {node->left = new TreeNode(0);que.push(node->left);leftQue.push(left);rightQue.push(mid - 1);}if(right >= mid + 1) {node->right = new TreeNode(0);que.push(node->right);leftQue.push(mid + 1);rightQue.push(right);}}return root;}
};思路2:递归,通过递归调用不断创建和给父节点接上新节点,完成二叉搜索树的构建,很明显,如果要高度平衡,那么left,mid,right三个下标是不可少的。
代码实现2:
class Solution {
public:TreeNode* traversal(vector<int> &nums, int left, int right) {if(left > right) return nullptr;int mid = left + ((right - left) / 2);TreeNode *root = new TreeNode(nums[mid]);root->left = traversal(nums, left, mid - 1);root->right = traversal(nums, mid + 1, right);return root;}TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode *root = traversal(nums, 0, nums.size() - 1);return root;}
};