二叉树理论基础：

https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

513.找树左下角的值

题目链接：https://leetcode.cn/problems/find-bottom-left-tree-value/

思路:（递归法）

首先要是最后一行，然后是最左边的值。
可以使用前序遍历（当然中序，后序都可以，因为本题没有 中间节点的处理逻辑，只要左优先就行），保证优先左边搜索，然后记录深度最大的叶子节点，此时就是树的最后一行最左边的值。
记得用一个int型的变量用来记录最大深度。

class Solution {private int MAX_DEEP = -1;private int value = 0;public int findBottomLeftValue(TreeNode root) {traversal(root,0);return value;}public void traversal(TreeNode node ,int depth){if(node == null)   return ;// 遇到叶子结点更新最大深度if(node.left == null && node.right == null){if(depth > MAX_DEEP){value = node.val;MAX_DEEP = depth;}}traversal(node.left,depth+1);traversal(node.right,depth+1);}
}

112. 路径总和

题目连接：https://leetcode.cn/problems/path-sum/description/

思路：

这道题我们要遍历从根节点到叶子节点的路径看看总和是不是目标和。
可以使用深度优先遍历的方式（本题前中后序都可以，无所谓，因为中节点也没有处理逻辑）来遍历二叉树。
本题我们要找一条符合条件的路径，所以递归函数需要返回值，及时返回。
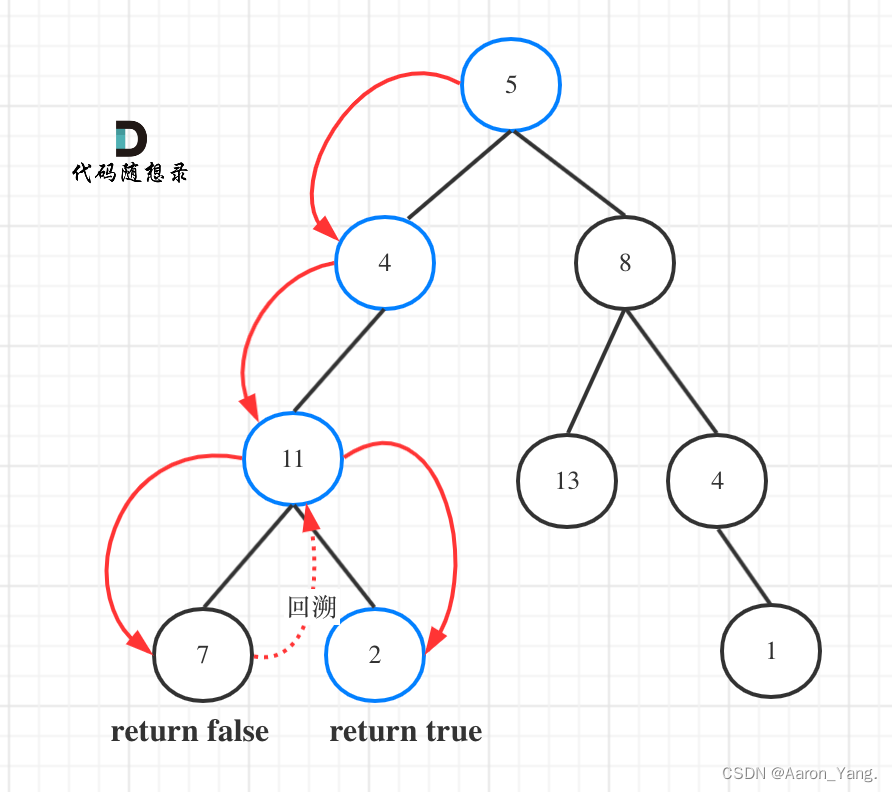图中可以看出，遍历的路线，并不要遍历整棵树，所以递归函数需要返回值，可以用boolean类型表示。
不要去累加然后判断是否等于目标和，那么代码比较麻烦，可以用递减，让计数器count初始为目标和，然后每次减去遍历路径节点上的数值。
如果最后count == 0，同时到了叶子节点的话，说明找到了目标和。
如果遍历到了叶子节点，count不为0，就是没找到。这里count，就直接用targetSum 来代替了。

class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if(root == null)return false;targetSum -= root.val;// 是叶子结点if(root.left == null && root.right == null)return targetSum == 0;if(root.left != null){boolean res = hasPathSum(root.left,targetSum) ;// 若存在某种情况，成立if(res)return true;}if(root.right != null){boolean res = hasPathSum(root.right,targetSum);if(res)return true;}return false;}}

113. 路径总和 ||

题目链接：https://leetcode.cn/problems/path-sum-ii/description/

思路：

113.路径总和ii要遍历整个树，找到所有路径，所以递归函数不要返回值！

class Solution {public List<List<Integer>> pathSum(TreeNode root, int targetSum) {List<List<Integer>> res = new ArrayList<>();if(root == null)return res;List<Integer> path = new LinkedList<>();traversal(root,targetSum,res,path);return res;}public void traversal(TreeNode node, int targetSum, List<List<Integer>> res, List<Integer>path){path.add(node.val);// 是否是叶子结点if(node.left == null && node.right == null){if(targetSum - node.val == 0){res.add(new ArrayList<>(path));}return ;}if(node.left != null){traversal(node.left,targetSum - node.val,res,path);path.remove(path.size()-1);}if(node.right != null){traversal(node.right,targetSum - node.val,res,path);path.remove(path.size()-1);}}
}

106.从中序与后序遍历序列构造二叉树

题目链接：https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/
类似题目：105.从前序与中序遍历序列构造二叉树

思路：

何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

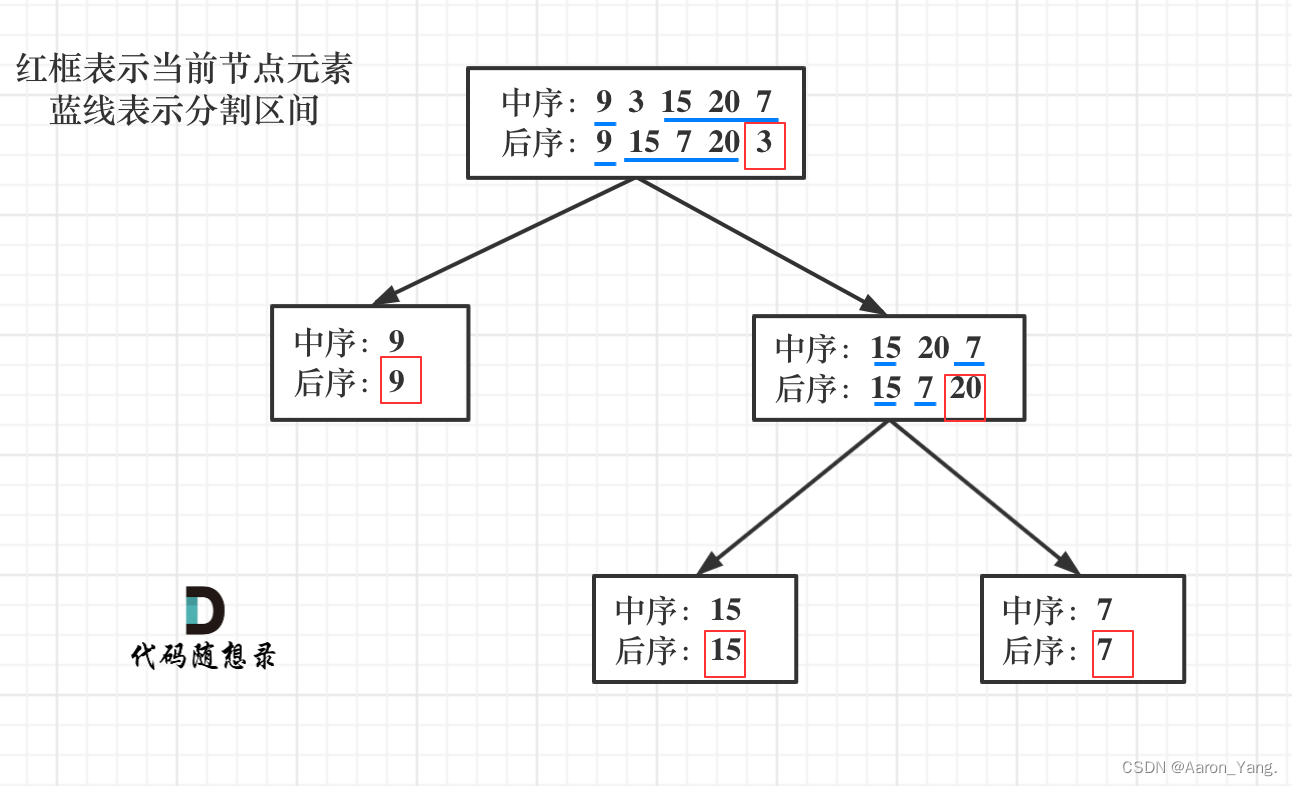
说到一层一层切割，就应该想到了递归。

来看一下一共分几步：

第一步：如果数组大小为零的话，说明是空节点了。

第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）

第五步：切割后序数组，切成后序左数组和后序右数组

第六步：递归处理左区间和右区间。

难点就是如何切割，以及边界值找不好很容易乱套。

在切割的过程中会产生四个区间，把握不好不变量的话，一会左闭右开，一会左闭右闭，必然乱套！

这里我们用的是左闭右开，中序数组比较好切割，根据后序遍历的最后一个元素来切割就行。

重点是后序数组的切割，首先最后一个元素肯定是不要了，这里我们可以根据中序数组切成的左中序数组和右中序数组，那么后序数组就可以按照左中序数组的大小来切割，切成左后序数组和右后序数组。

接下来可以递归了，然后代码也就出来了。

class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {if(postorder.length == 0 || inorder.length == 0)return null;return buildHelper(inorder,0,inorder.length,postorder,0,postorder.length);}public TreeNode buildHelper(int[] inorder,int inorderStart, int inorderEnd,int[] postorder,int postorderStart, int postorderEnd){if(postorderStart == postorderEnd)return null;// 根节点int rootVal = postorder[postorderEnd -1];TreeNode root = new TreeNode(rootVal);// 中序遍历中的根节点int middleIndex;for(middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++){if(inorder[middleIndex] == rootVal)break;}// 切割中序数组// 中序左区间，左闭右开 [leftInorderStart, leftInorderEnd)int leftInorderStart = inorderStart;int leftInorderEnd = middleIndex;// 中序右区间，左闭右开 [rightInorderStart, rightInorderEnd)int rightInorderStart = middleIndex + 1;int rightInorderEnd = inorderEnd;// 切割后序数组// 后序左区间，左闭右开[leftPostorderStart, leftPostorderEnd)int leftPostorderStart = postorderStart;int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);// 后序右区间，左闭右开int rightPostorderStart = leftPostorderEnd;int rightPostorderEnd = postorderEnd - 1;// System.out.println(rightPostorderStart+" "+rightPostorderEnd);root.left = buildHelper(inorder,leftInorderStart,leftInorderEnd,postorder,leftPostorderStart,leftPostorderEnd);root.right = buildHelper(inorder,rightInorderStart,rightInorderEnd,postorder,rightPostorderStart,rightPostorderEnd);return root;}
}