目录
一、思维导图
二、 物理层概述
1.物理层概述
2.四大特性(巧记"械气功程")
三、通信基础
1.数据通信基础
2.趁热打铁☞习题训练
3.信号の变身:编码与调制
4.极限数据传输率
5.趁热打铁☞习题训练
6.信道复用技术
推荐
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站
一、思维导图

二、 物理层概述
1.物理层概述
在连接各种计算机的传输媒体上传输数据比特流,确定与传输媒体接口有关的一些特性
2.四大特性(巧记"械气功程")

(1)机械特性
定义物理连接的特性,规定物理连接时所采用的规格、接口形状、引线数目、引脚数量和排列情况
(2)电气特性
规定传输二进制位时,线路上信号的电压范围、阻抗匹配、传输速率和距离限制等(某网络在物理层规定,信号的电平用+10V~ +15V表示二进制0,用-10V~-15V表示二进制1,电线长度限于15m以内)
(3)功能特性
指明某条线上出现的某一电平表示何种意义,接口部件的信号线的用途
(4)规程特性
(过程特性)定义各条物理线路的工作规程和时序关系
三、通信基础
1.数据通信基础
码元是指用一个固定时长的信号波形(数字脉冲),代表不同离散数值的基本波形,是数字通信中数字信号的计量单位,这个时长内的信号称为k进制码元,而该时长称为码元宽度。当码元的离散状态有M个时(M大于2),此时码元为M进制码元

码元传输速率(波特率),是单位时间内传输的码元个数,单位是波特Baud(B)
消息:通信的目的是传送消息,如语音、文字、图像、视频等。
数据:数据是运送消息的实体。0/1
信号:信号是数据的电气或电磁的表现。
信道:表示向某一个方向传送信息的媒体。
单工通信:广播
半双工通信:对讲机
全双工通信:打电话
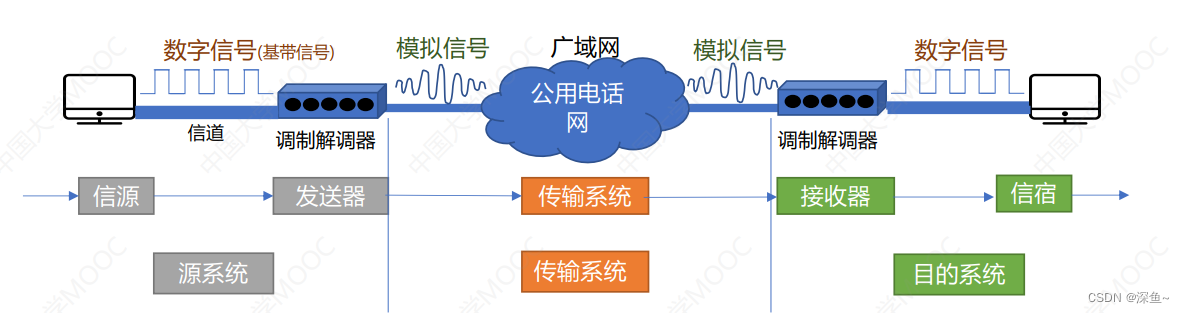
基带信号:来自信源的信号。
基带信号の变身:
(1)编码(基带调制):变成数字信号
(2)带通调制:变成模拟信号(带通信号)
2.趁热打铁☞习题训练
已知八进制数字信号的传输速率为1600B。试问变换成二进制数字信号时的传输速率是多少?
答:
B——表示波特(速度单位)、Byte(存储单位)
八进制:一个码元对等三个比特信息(对8取以2为底的对数即可)
二进制:一个码元对等一个比特信息
所以就是1600*3=4800B/s
3.信号の变身:编码与调制
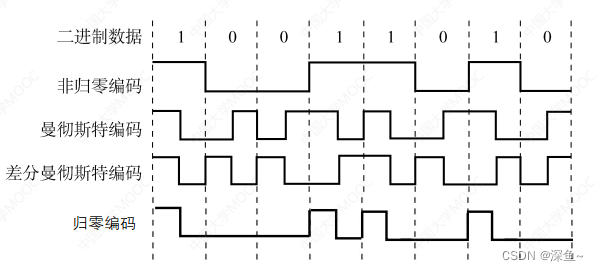
常用编码方式:
(1)归零编码:高1低0,后半段归零
(2)非归零编码:高1低0,后半段不归零
(3)曼彻斯特编码:前高后低->1/0 前低后高->0/1
(4)差分曼彻斯特编码:跳变为0,不变为1(看初始是否会跳变)
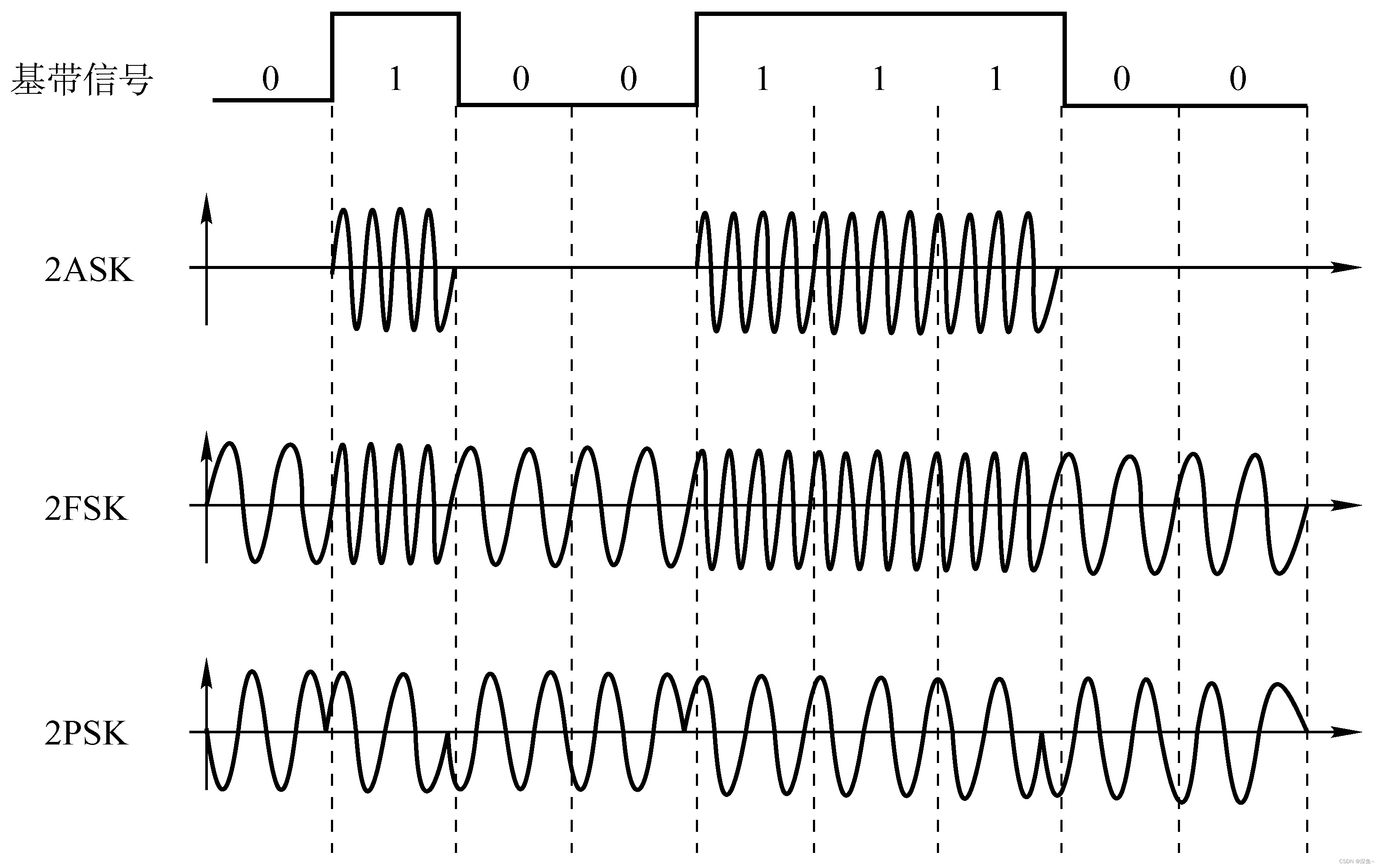
常用带通调制方式:
(1)调幅(AM-Amplitude Modulation)
(2)调频(FM-Frequency modulation)
(3)调相(PM-Phase modulation)
(4)正交振幅调制(QAM,调幅+调相)
4.极限数据传输率
(1)奈氏准则:在理想低通(无噪声,带宽受限)条件下,极限码元传输速率为 2W Baud,W是信道带宽,单位是Hz,V是每个码元离散电平的数目(即有多少种码元)

(2)香农定理:在带宽受限且有噪声的信道中,为了不产生误差,信息的数据传输速率有上限值
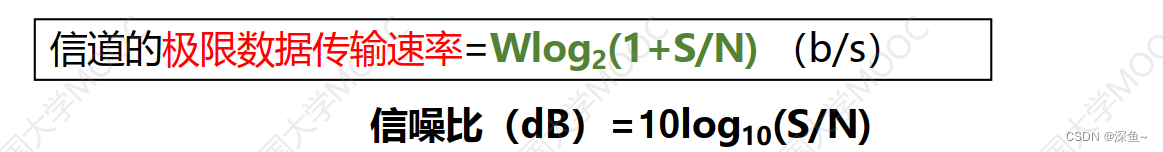
5.趁热打铁☞习题训练
例. 电话系统的典型参数是信道带宽为3000Hz,信噪比为30dB,则该系统最大数据传输速率是多少?
答:给了信噪比用香农定理
6.信道复用技术
多路复用技术:
把多个信号组合在一条物理信道上进行传输,使得多个计算机或终端设备共享信道资源,提高信道利用率。把一条广播信道,逻辑上分成几条用于两个节点之间通信的互不干扰的子信道,实际就是把广播信道转变为点对点信道

(1) 频分多路复用 FDM
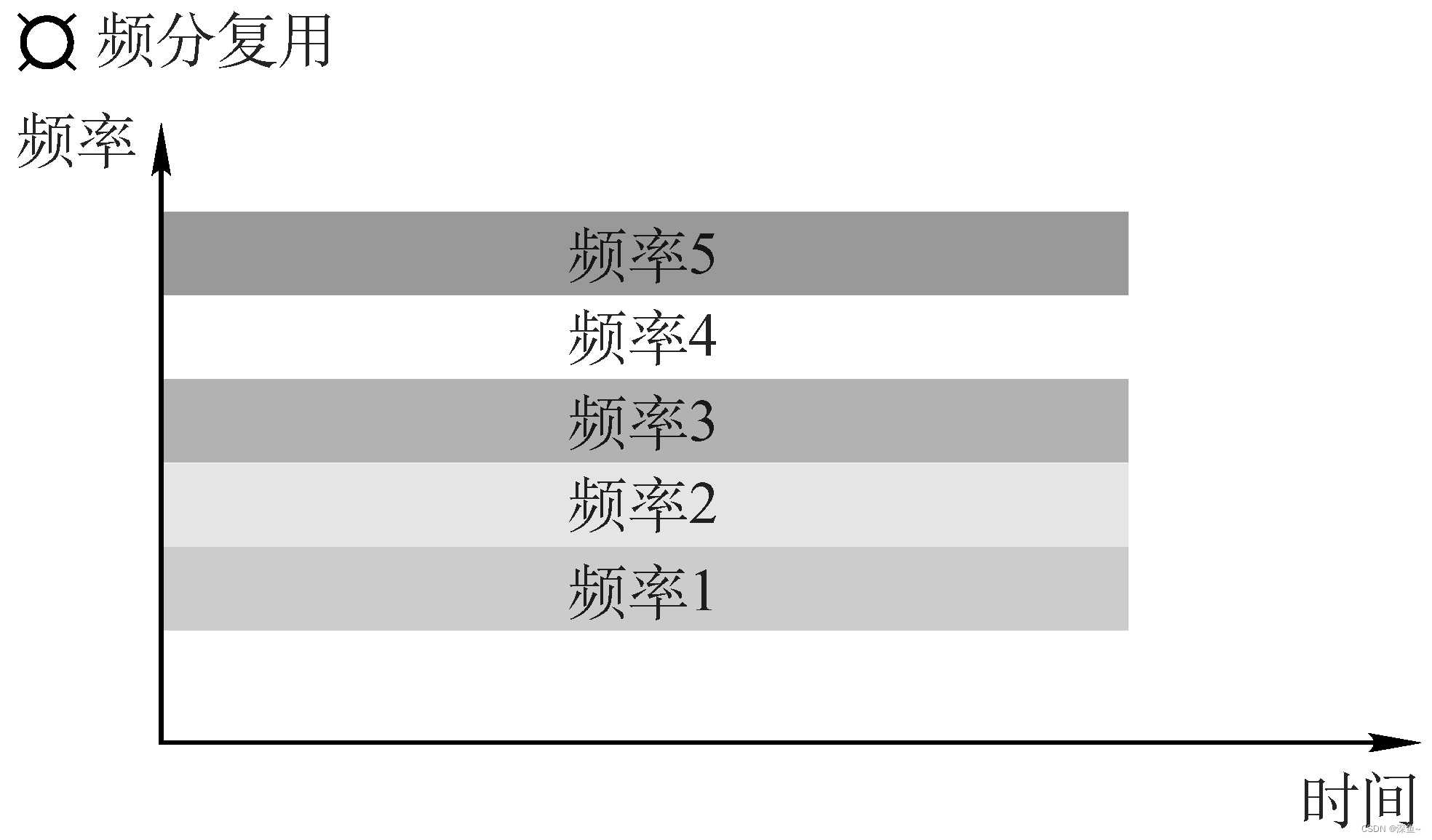
(2)时分多路复用 TDM


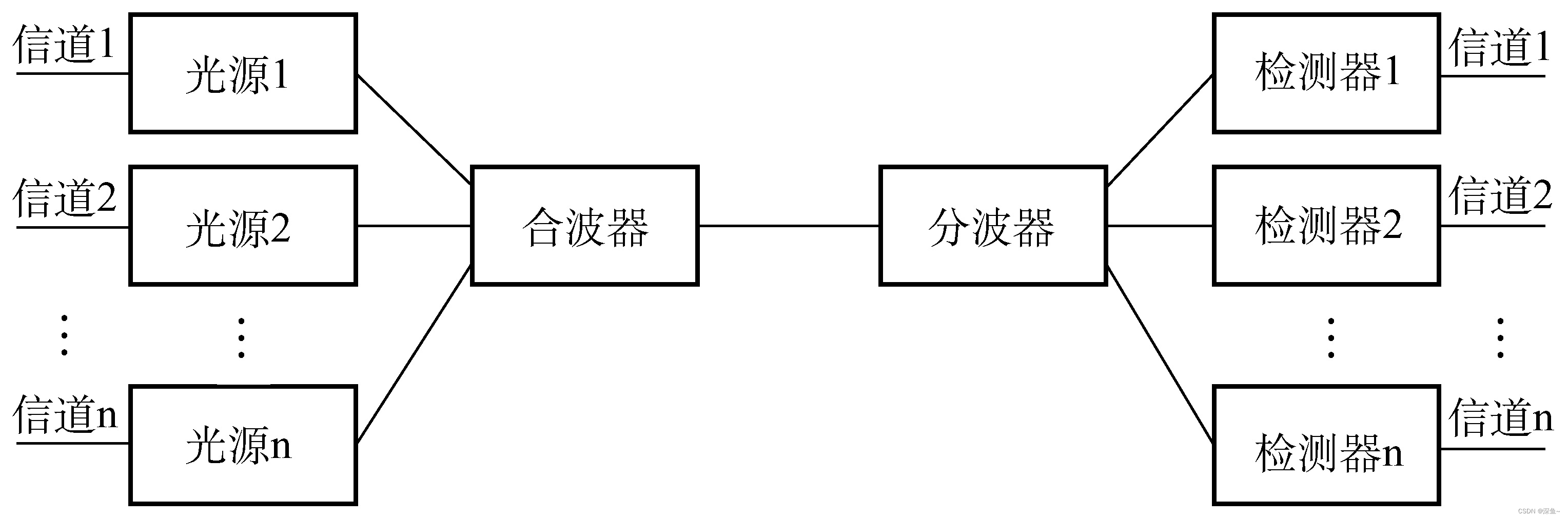
(3) 波分多路复用
波分多路复用就是光的频分多路复用,在一根光纤中传输多种不同波长(频率)的光信号,由于波长(频率)不同,所以各路光信号互不干扰,最后再用波长分解复用器将各路波长分解出来