导言
在机器学习领域,线性回归是最基础且重要的算法之一。它用于建立输入特征与输出目标之间的线性关系模型,为我们解决回归问题提供了有效的工具。本文将详细介绍线性回归的原理、应用和实现方法,帮助读者快速了解和上手这一强大的机器学习算法。
一、线性回归简介
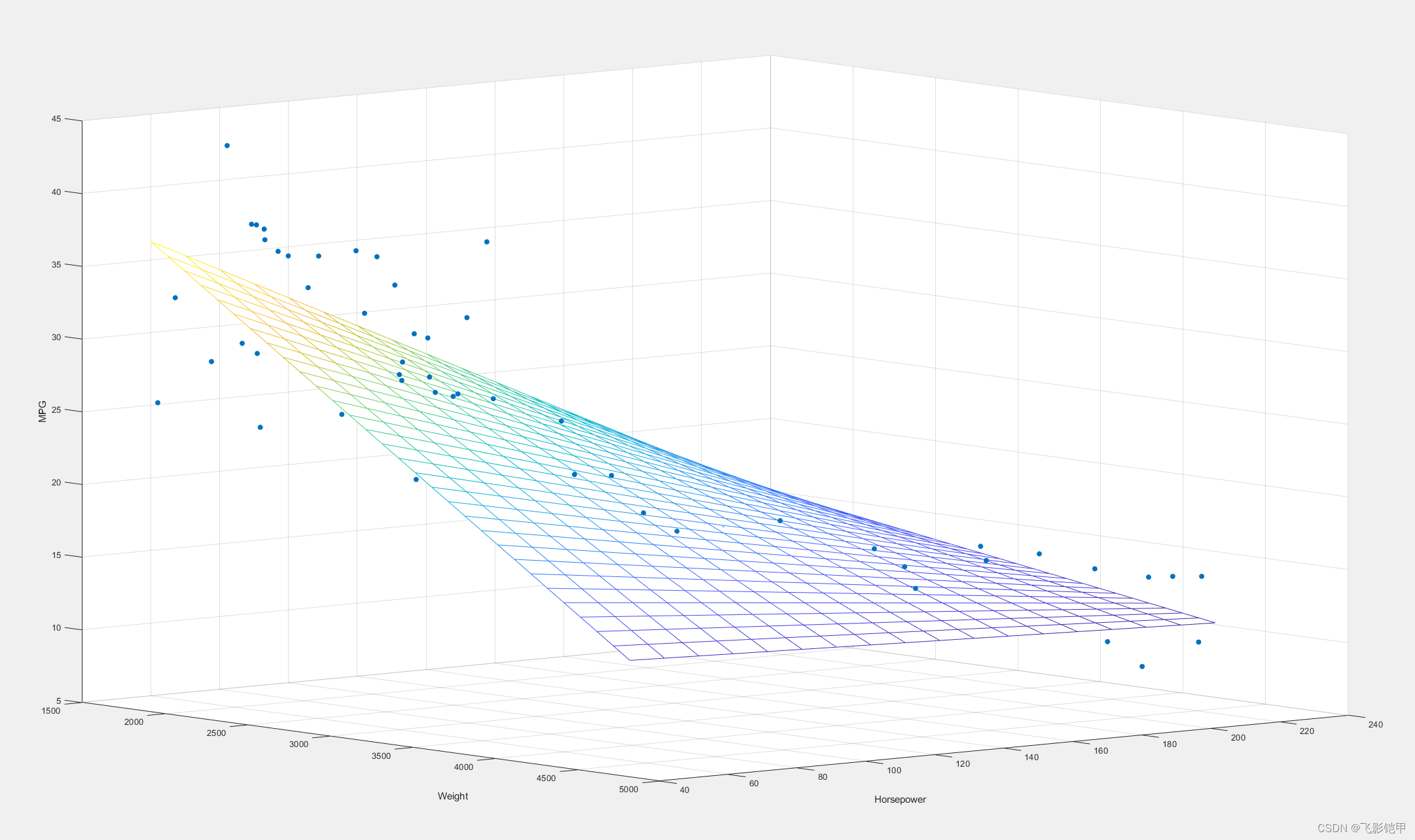
线性回归是一种监督学习算法,适用于处理连续数值预测问题。其基本思想是通过拟合最佳直线(或超平面)来预测输出变量与输入特征之间的关系。线性回归的目标是找到最优的模型参数,使得模型对训练数据的预测值与真实值之间的误差最小化。
二、线性回归原理
-
假设函数 线性回归假设输入特征与输出目标之间存在线性关系,即数学上的假设函数为:y = w0 + w1x1 + w2x2 + ... + wn*xn,其中y为输出目标,x1, x2, ..., xn为输入特征,w0, w1, w2, ..., wn为模型参数。
-
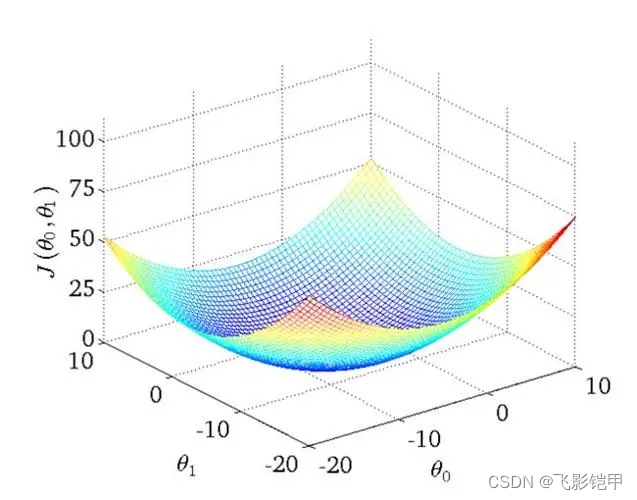
损失函数 为了优化模型参数,需要定义一个损失函数来衡量预测值与真实值之间的误差。常用的损失函数是均方误差(Mean Square Error,MSE),其定义为:MSE = 1/N * Σ(yi - ŷi)^2,其中N为样本数量,yi为真实值,ŷi为模型的预测值。
-
参数优化 线性回归使用梯度下降等优化算法来最小化损失函数。梯度下降通过计算损失函数对各个参数的偏导数,更新参数值以使损失函数逐步减小,直到达到最小值。
三、应用场景
线性回归广泛应用于各个领域,以下是一些常见的应用场景:
- 房价预测:根据房屋的各项特征(如面积、地理位置等),预测其价格。
- 销售预测:通过历史销售数据和市场因素,预测未来销售额。
- 股票市场分析:基于公司财务指标和宏观经济数据,预测股票价格的变动趋势。
- 广告投放优化:根据广告投放渠道、受众特征等因素,预测广告的点击率和转化率。
四、实现方法
-
传统方法: a. 最小二乘法:通过最小化残差平方和来求解模型参数,得到闭式解。 b. 梯度下降法:迭代更新模型参数,直至收敛到最优解。
-
机器学习库: a. Scikit-learn:提供了线性回归模型的实现,使用简单且效果良好。 b. TensorFlow、PyTorch等深度学习框架:可以通过神经网络构建更复杂的线性回归模型,具有更强的拟合能力。
结语
线性回归是机器学习领域中最基础和常用的算法之一。通过本文的介绍,我们了解了线性回归的原理、应用场景和实现方法。希望读者能够掌握线性回归算法,并能在实际问题中灵活运用。