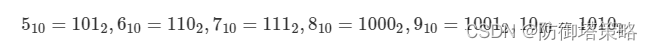C++ 位图布隆过滤器哈希切割-编程知识

文章目录

位图
- 概念
- 模拟实现
- 海量数据面试题1
布隆过滤器
- 模拟实现
- 应用场景
- 海量数据面试题2
哈希切割
- 海量数据面试题3

位图

概念

我们用一道题引出此概念：

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中

分析：40亿无符号整数占多大空间？16G —— 如果将这些整形数据尽数导入内存中再用诸如遍历、排序后二分查找等方式处理，空间上多少会吃不消
既然想节省空间，又只是判断数据是否存在，我们可以考虑借助更小的数据单位位(bit) 去表示存在与否(1/0)：

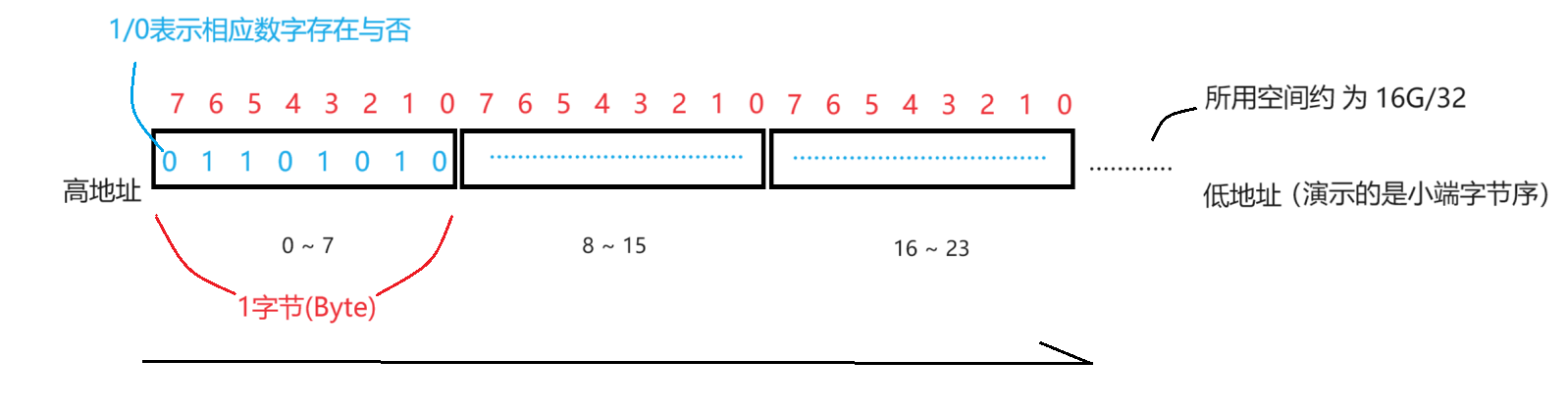
在这里插入图片描述

所谓位图，就是这样用每一位来存放某种状态的结构。适用于海量数据，数据无重复的场景

模拟实现

//位图
template<size_t N>//非类型模板参数，用于指示位图范围
class bitset {
public:bitset() {_bits.resize(N / 8 + 1, 0);}//插入void set(size_t data) {int i = data / 8;//是第几个charint j = data % 8;//是char里的第几个数据_bits[i] |= (1 << j);}//删除void reset(size_t data) {int i = data / 8;int j = data % 8;_bits[i] &= ~(1 << j);}bool test(size_t data) {int i = data / 8;int j = data % 8;return _bits[i] & (1 << j);}
private:vector<char> _bits;//存储char，使用其中的每个bit
};

海量数据面试题1

100亿个整数，找出其中只出现一次的整数？

以上我们用 1/0 表示存在与否，稍作延伸我们可以用 10 / 01 / 00 表示出现 2 / 1 / 0 次

//复用位图解决问题
template<size_t N>
class twobitset
{
public:void set(size_t x){// 00 -> 01if (_bs1.test(x) == false&& _bs2.test(x) == false){_bs2.set(x);}// 01 -> 10else if (_bs1.test(x) == false&& _bs2.test(x) == true){_bs1.set(x);_bs2.reset(x);}// 10}void Print(){for (size_t i = 0; i < N; ++i){if (_bs2.test(i)){cout << i << endl;}}}
public:bitset<N> _bs1;bitset<N> _bs2;
};

两个文件分别有100亿个整数，如何在只有1G内存的情况下求得它们的交集

思路1：先将一个文件中的数据导入位图中，然后看第二个文件，每次找到交集数据时将位图中相应位置reset，防止输出重复数据
思路2：分别用两个位图存储两文件中的数据，从 0 遍历到 -1（对于无符号整形而言就是相应的最大值），看两个位图中是否都有相应数据

布隆过滤器

大量的数据如果用哈希表存储，会很浪费空间，于是我们用位图处理，但位图一般只能处理整形，面对字符串无能为力，但如果运用哈希的思想的话……

于是将哈希（将数据转换为整形并计算映射位置）与位图（用位1 / 0去表示数据的存在与否）结合，即布隆过滤器

因为只是用位表示数据的存在与否而非记录数据，所以如果遇上哈希冲突的话是没办法处理的，于是只能想办法减少哈希冲突：让一个数据映射到多个位置

示例：用不同的哈希函数将数据映射到不同的位置（感谢Yang Chen大佬的图(?)）

可以看出，这种做法使得布隆过滤器在查找数据时，如果 返回结果为该数据存在，则不一定真的存在，但若返回不存在，则一定不存在

模拟实现

//让一个数据映射三个位置（需要三个哈希/散列函数）
//暂时不用太在意这三个仿函数用的是什么逻辑
struct BKDRHash
{size_t operator()(const string& s){size_t hash = 0;for (auto ch : s){hash += ch;hash *= 31;}return hash;}
};
struct APHash
{size_t operator()(const string& s){size_t hash = 0;for (long i = 0; i < s.size(); i++){size_t ch = s[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}
};
struct DJBHash
{size_t operator()(const string& s){size_t hash = 5381;for (auto ch : s){hash += (hash << 5) + ch;}return hash;}
};// N最多会插入key数据的个数
template<size_t N,class K = string,	//默认支持stringclass Hash1 = BKDRHash,class Hash2 = APHash,class Hash3 = DJBHash>
class BloomFilter
{
public://插入void set(const K& key){size_t len = N * _X;size_t hash1 = Hash1()(key) % len;_bs.set(hash1);size_t hash2 = Hash2()(key) % len;_bs.set(hash2);size_t hash3 = Hash3()(key) % len;_bs.set(hash3);}//查找bool test(const K& key){size_t len = N * _X;size_t hash1 = Hash1()(key) % len;if (!_bs.test(hash1)){return false;}size_t hash2 = Hash2()(key) % len;if (!_bs.test(hash2)){return false;}size_t hash3 = Hash3()(key) % len;if (!_bs.test(hash3)){return false;}// 在      不准确的，存在误判// 不在    准确的return true;}
private:static const size_t _X = 6;//为减少哈希冲突，提前确定每有一个数据，就多_X个位（经后面的测试发现6的效果不错）bitset<N* _X> _bs;		   
};

测试误判率：

//老师用于测试布隆过滤器的示例：
void test_bloomfilter()
{srand(time(0));const size_t N = 10000;BloomFilter<N> bf;std::vector<std::string> v1;std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";//随便找一个网址for (size_t i = 0; i < N; ++i){v1.push_back(url + std::to_string(i));//在网址字符串后加不同的东西使得插入的数据不同}for (auto& str : v1){bf.set(str);}// v2跟v1是相似字符串集，但是不一样std::vector<std::string> v2;for (size_t i = 0; i < N; ++i){std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";url += std::to_string(999999 + i);v2.push_back(url);//可以看出，v2存储的数据前面网址部分的字符串和v1存储的数据都是一样的（相似字符串）}size_t n2 = 0;for (auto& str : v2){if (bf.test(str)){++n2;}}cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;// 不相似字符串集std::vector<std::string> v3;for (size_t i = 0; i < N; ++i){string url = "zhihu.com";//string url = "https://www.cctalk.com/m/statistics/live/16845432622875";url += std::to_string(i + rand());v3.push_back(url);//可以看出，v3存储的数据和v1一点都不相似}size_t n3 = 0;for (auto& str : v3){if (bf.test(str)){++n3;}}cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
}