题目
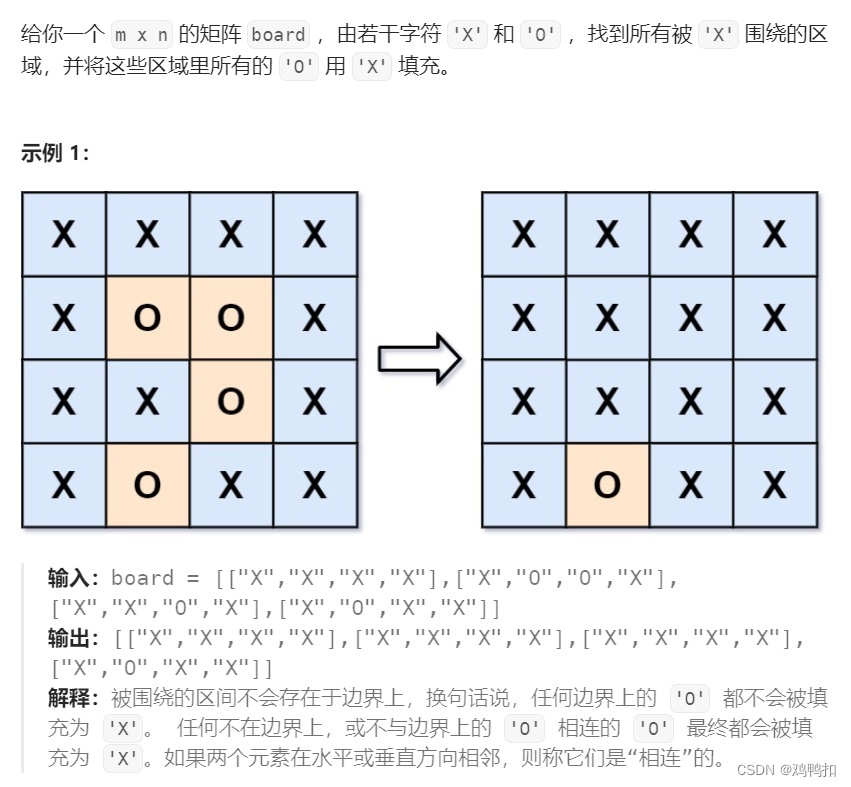
注意:
1 <= m, n <= 200
board[i][j] 为 ‘X’ 或 ‘O’
思路
根据一般网格结构上的DFS,或者说岛屿问题,第一反应很容易想到找出所有的‘O’然后开始DFS遍历,改为‘X’。
但是这里有个联通的问题,如果这个‘O’是边界上的‘O’或者与边界上的‘O’联通,那么它实际上不应该被改为‘X’。
为此我们应该先预处理,从边界上的‘O’出发进行DFS遍历,找出所有与其相连的‘O’,这个过程中为了保证DFS不陷入死循环,我们要将遍历过的‘O’改掉,但是不能改为‘X’,因为最后我们是要把这些‘O’再复原回去的,如果我们改为了‘X’,之后就无法找出具体哪些节点要复原了,所以这里用另外的字母‘N’代替。
预处理后还剩下的‘O’则是与边界的‘O’不连通的点了,我们正常DFS遍历并改为‘X’。
最后则是将所有的‘N’再改回‘O’。
代码
初版代码
class Solution {public void solve(char[][] board) {int m = board.length;int n = board[0].length;//1.预处理边界的O,让其等于N,且从其dfs遍历的点都变为Nfor(int r = 0;r<m;r++){if(board[r][0]=='O') {dfs(board,r,0,'N');}if(board[r][n-1]=='O') {dfs(board,r,n-1,'N');}}for(int c=0;c<n;c++){if(board[0][c]=='O') {dfs(board,0,c,'N');}if(board[m-1][c]=='O') {dfs(board,m-1,c,'N');}}//2.遍历剩下所有的O,从其开始出发dfs遍历for(int r=0;r<m;r++){for(int c=0;c<n;c++){if(board[r][c]=='O')dfs(board,r,c,'X');}}//3.将所有的N换回O。for(int r=0;r<m;r++){for(int c=0;c<n;c++){if(board[r][c]=='N')board[r][c]='O';}}}public void dfs(char[][] board, int r,int c,char type){//为了让边界的O的dfs和不与边界O联通的O的dfs都用同一个函数,这里多加了一个参数type,如果传入的是N,那么说明是前者的dfs,最后点要改为N。如果传入的是X,说明是后者的dfs。最后点要改为X。//判断边界情况if(!ifCouldVis(board,r,c)) return;board[r][c]=type;dfs(board,r+1,c,type);dfs(board,r,c+1,type);dfs(board,r-1,c,type);dfs(board,r,c-1,type);}public boolean ifCouldVis(char[][] board,int r,int c){return r>=0 && c>=0 && r<board.length && c<board[0].length && board[r][c]=='O';}
}
4ms,击败17.92%使用 Java 的用户。说明还需要优化。
第二版代码
根据思路发现第一版代码存在三步。
- 找出所有边界上的O,用DFS找出与其联通的O点,将其改为N
- 找出剩下的所有O,用DFS找出与其联通的O点,将其改为X
- 还原所有的N为O
我们发现第二步的DFS是多余的,因为我们只需要把剩下所有的O改为X即可,不需要找出与其联通的O点。那么第二步的代码应该由
//2.遍历剩下所有的O,从其开始出发dfs遍历for(int r=0;r<m;r++){for(int c=0;c<n;c++){if(board[r][c]=='O')dfs(board,r,c,'X');}}
变更为
//2.遍历剩下所有的O,从其开始出发dfs遍历for(int r=0;r<m;r++){for(int c=0;c<n;c++){if(board[r][c]=='O')board[r][c]='X';}}
此时再测效率,1ms,击败99.81%使用 Java 的用户
但是既然第二步的dfs没有了,那么传入的type参数也没用了。我们也不需要第二步和第三步分别在两个循环中,直接合并为一个循环即可,因为两层for循环是从上到下,从左到右依次循环的,所以第三步改回去的‘O’不会影响到第二步的‘O’的判断·。最终代码如下:
class Solution {public void solve(char[][] board) {int m = board.length;int n = board[0].length;//1.预处理边界的O,让其等于N,且从其dfs遍历的点都变为Nfor(int r = 0;r<m;r++){if(board[r][0]=='O') {dfs(board,r,0);}if(board[r][n-1]=='O') {dfs(board,r,n-1);}}for(int c=0;c<n;c++){if(board[0][c]=='O') {dfs(board,0,c);}if(board[m-1][c]=='O') {dfs(board,m-1,c);}}//2.遍历整个网格,因为两层for循环是从上到下,从左到右依次循环的,所以由‘N’改回去的‘O’不会影响到原来不连通的‘O’的判断·for(int r=0;r<m;r++){for(int c=0;c<n;c++){if(board[r][c]=='O') board[r][c]='X';if(board[r][c]=='N') board[r][c]='O';}}}public void dfs(char[][] board, int r,int c){//判断边界情况if(!ifCouldVis(board,r,c)) return;board[r][c]='N';dfs(board,r+1,c);dfs(board,r,c+1);dfs(board,r-1,c);dfs(board,r,c-1);}public boolean ifCouldVis(char[][] board,int r,int c){return r>=0 && c>=0 && r<board.length && c<board[0].length && board[r][c]=='O';}
}
效率没有变动,依旧是1ms,但是代码简洁了很多。