PAC
主成分分析(Principal Component Analysis)
- 一个非监督的机器学习算法
- 主要用于数据的降维
- 通过降维,可以发现更便于人类理解的特征
- 其他应用:可视化;去噪

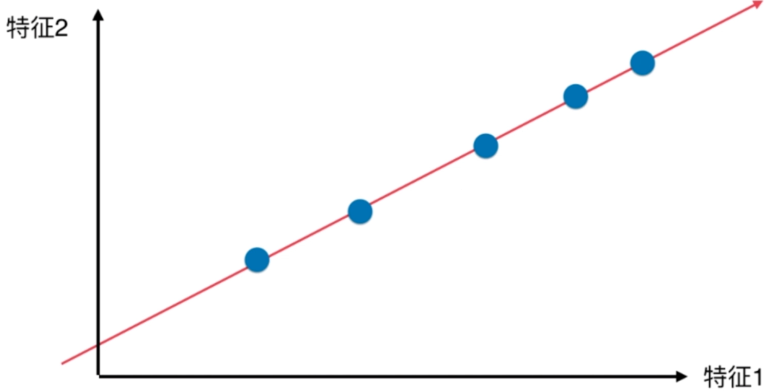
如何找到这个让样本间间距最大的轴?
如何定义样本间间距?

找到一个轴,使得样本空间的所有点映射到这个轴后,方差最大
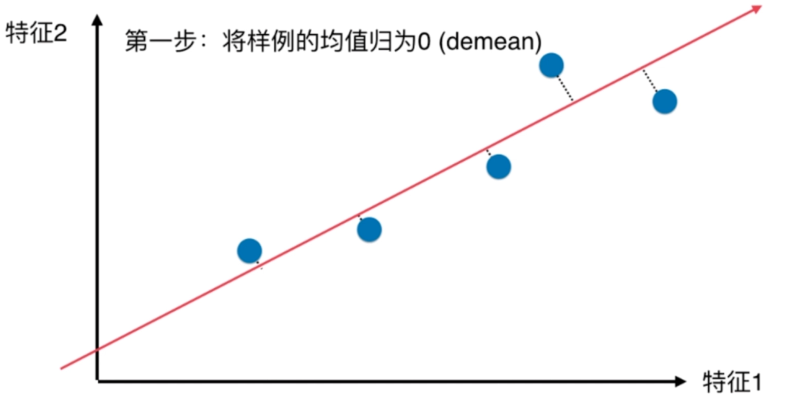
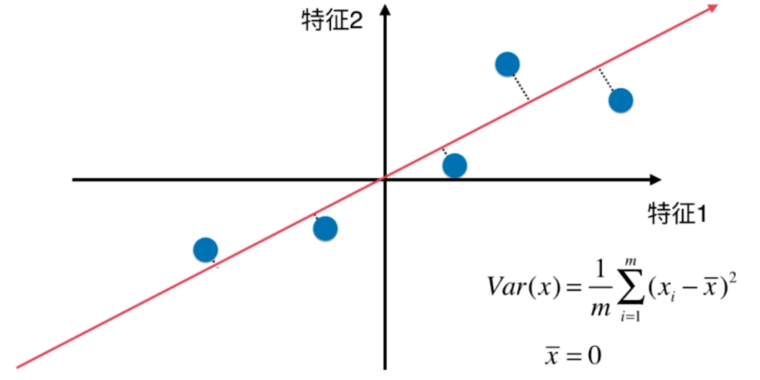
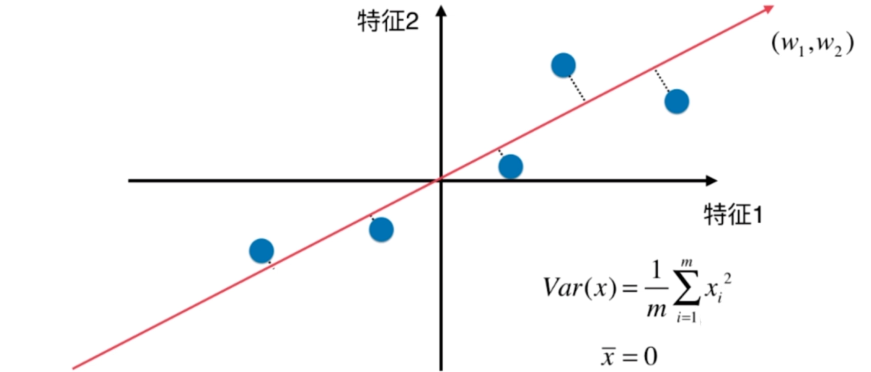


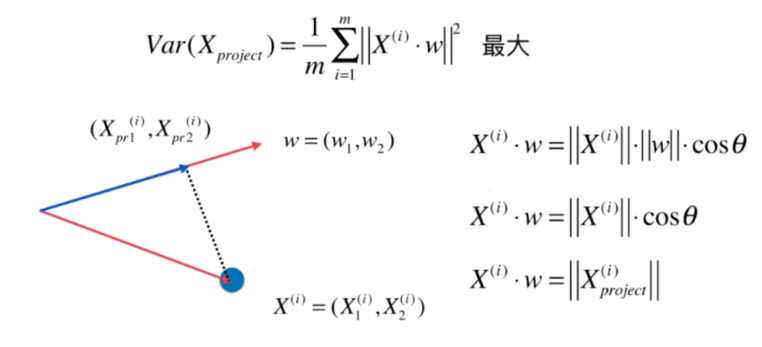
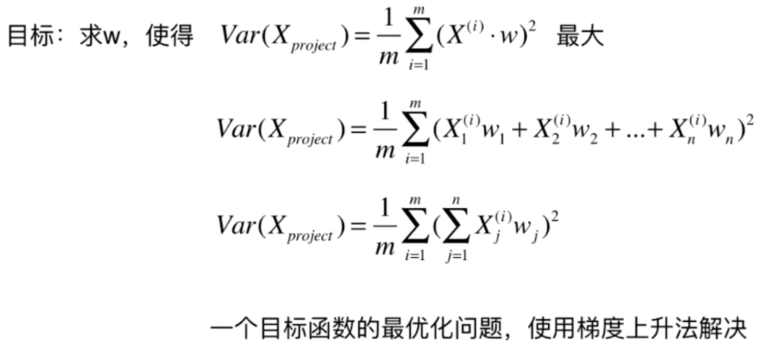
梯度上升法解决主成分分析问题
主成分分析

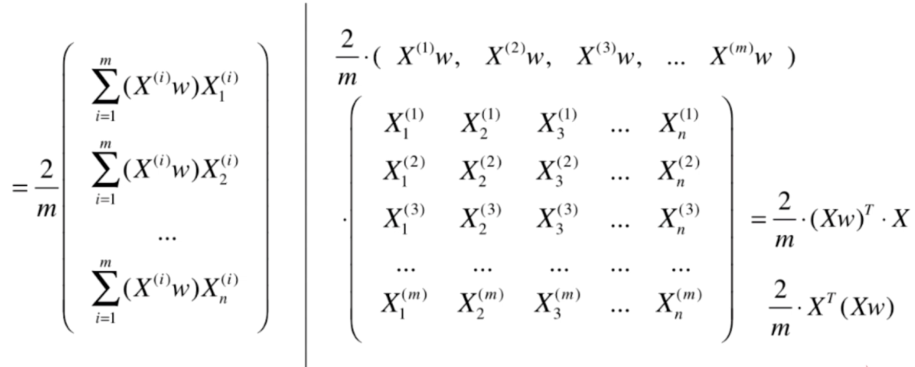
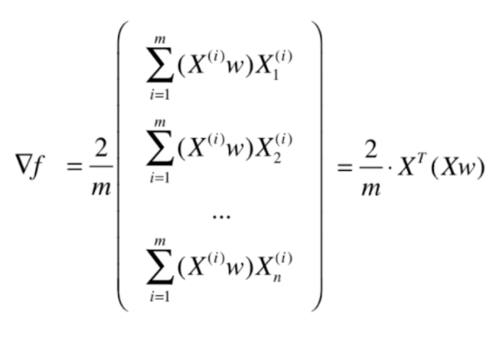
代码实现
生成测试用例
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)
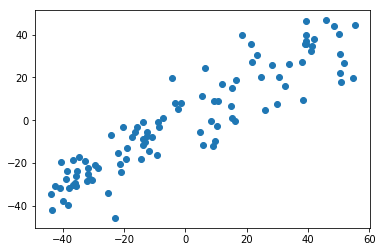
plt.scatter(X[:,0], X[:,1])
plt.show()
demean
def demean(X):return X - np.mean(X, axis=0)
X_demean = demean(X)
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.show()
梯度上升法
def f(w, X):return np.sum((X.dot(w)**2)) / len(X)def df_math(w, X):return X.T.dot(X.dot(w)) * 2. / len(X)def df_debug(w, X, epsilon=0.0001):res = np.empty(len(w))for i in range(len(w)):w_1 = w.copy()w_1[i] += epsilonw_2 = w.copy()w_2[i] -= epsilonres[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)return resdef direction(w):return w / np.linalg.norm(w)def gradient_ascent(df, X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):w = direction(initial_w) cur_iter = 0while cur_iter < n_iters:gradient = df(w, X)last_w = ww = w + eta * gradientw = direction(w) # 注意1:每次求一个单位方向if(abs(f(w, X) - f(last_w, X)) < epsilon):breakcur_iter += 1return w
initial_w = np.random.random(X.shape[1]) # 注意2:不能用0向量开始
eta = 0.001
# 注意3: 不能使用StandardScaler标准化数据
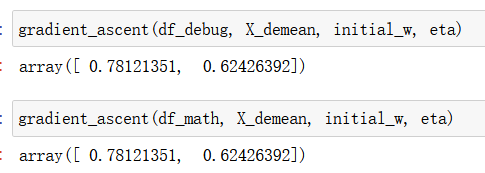
gradient_ascent(df_debug, X_demean, initial_w, eta)
gradient_ascent(df_math, X_demean, initial_w, eta)
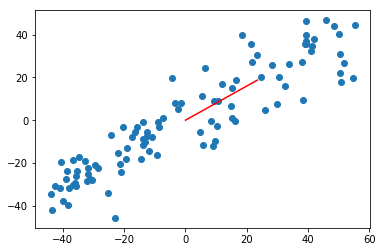
w = gradient_ascent(df_math, X_demean, initial_w, eta)
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.plot([0, w[0]*30], [0, w[1]*30], color='r')
plt.show()
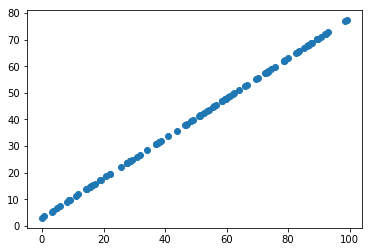
使用极端数据集测试
X2 = np.empty((100, 2))
X2[:,0] = np.random.uniform(0., 100., size=100)
X2[:,1] = 0.75 * X2[:,0] + 3.
plt.scatter(X2[:,0], X2[:,1])
plt.show()
X2_demean = demean(X2)
w2 = gradient_ascent(df_math, X2_demean, initial_w, eta)
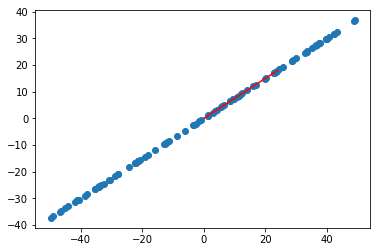
plt.scatter(X2_demean[:,0], X2_demean[:,1])
plt.plot([0, w2[0]*30], [0, w2[1]*30], color='r')
plt.show()
求数据的前n个主成分
求出第一主成分以后,如何求出下一个主成分?
数据进行改变,将数据在第一个主成分上的分量去掉
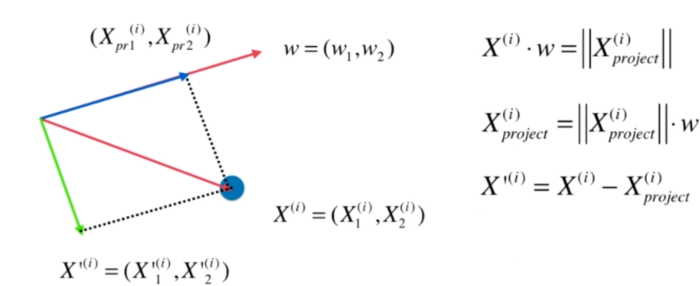
在新的数据上求第一主成分
代码
生成数据
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)
def demean(X):return X - np.mean(X, axis=0)
X = demean(X)
plt.scatter(X[:,0], X[:,1])
plt.show()
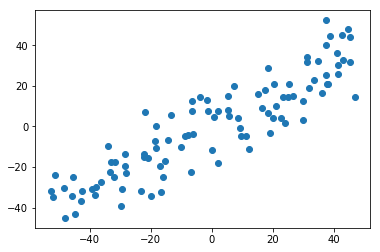
求出第一主成分
def f(w, X):return np.sum((X.dot(w)**2)) / len(X)def df(w, X):return X.T.dot(X.dot(w)) * 2. / len(X)def direction(w):return w / np.linalg.norm(w)def first_component(X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):w = direction(initial_w) cur_iter = 0while cur_iter < n_iters:gradient = df(w, X)last_w = ww = w + eta * gradientw = direction(w) if(abs(f(w, X) - f(last_w, X)) < epsilon):breakcur_iter += 1return w
initial_w = np.random.random(X.shape[1])
eta = 0.01
w = first_component(X, initial_w, eta)
求第二主成分
X2 = np.empty(X.shape)
for i in range(len(X)):X2[i] = X[i] - X[i].dot(w) * w
plt.scatter(X2[:,0], X2[:,1])
plt.show()
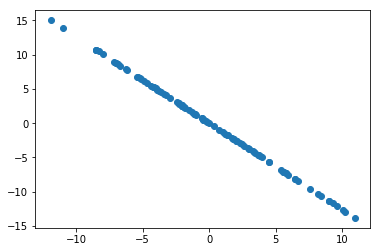
X2 = X - X.dot(w).reshape(-1, 1) * w
plt.scatter(X2[:,0], X2[:,1])
plt.show()
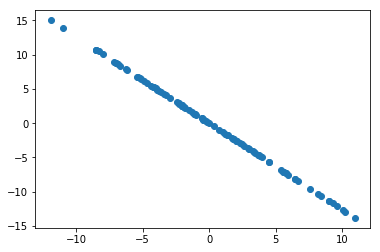
w2 = first_component(X2, initial_w, eta)

w.dot(w2)
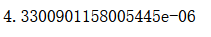
def first_n_components(n, X, eta=0.01, n_iters = 1e4, epsilon=1e-8):X_pca = X.copy()X_pca = demean(X_pca)res = []for i in range(n):initial_w = np.random.random(X_pca.shape[1])w = first_component(X_pca, initial_w, eta)res.append(w)X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * wreturn res
first_n_components(2, X)

高维数据向低维数据映射
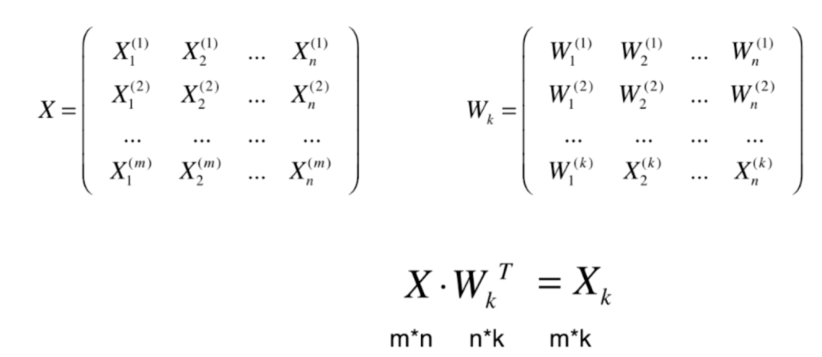
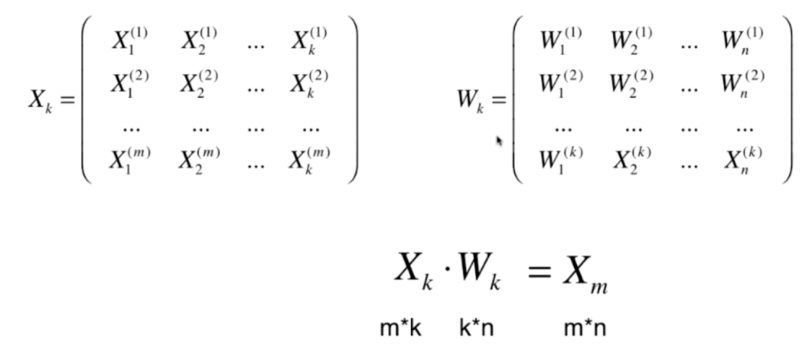
代码实现
import numpy as npclass PCA:def __init__(self, n_components):"""初始化PCA"""assert n_components >= 1, "n_components must be valid"self.n_components = n_componentsself.components_ = Nonedef fit(self, X, eta=0.01, n_iters=1e4):"""获得数据集X的前n个主成分"""assert self.n_components <= X.shape[1], \"n_components must not be greater than the feature number of X"def demean(X):return X - np.mean(X, axis=0)def f(w, X):return np.sum((X.dot(w) ** 2)) / len(X)def df(w, X):return X.T.dot(X.dot(w)) * 2. / len(X)def direction(w):return w / np.linalg.norm(w)def first_component(X, initial_w, eta=0.01, n_iters=1e4, epsilon=1e-8):w = direction(initial_w)cur_iter = 0while cur_iter < n_iters:gradient = df(w, X)last_w = ww = w + eta * gradientw = direction(w)if (abs(f(w, X) - f(last_w, X)) < epsilon):breakcur_iter += 1return wX_pca = demean(X)self.components_ = np.empty(shape=(self.n_components, X.shape[1]))for i in range(self.n_components):initial_w = np.random.random(X_pca.shape[1])w = first_component(X_pca, initial_w, eta, n_iters)self.components_[i,:] = wX_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * wreturn selfdef transform(self, X):"""将给定的X,映射到各个主成分分量中"""assert X.shape[1] == self.components_.shape[1]return X.dot(self.components_.T)def inverse_transform(self, X):"""将给定的X,反向映射回原来的特征空间"""assert X.shape[1] == self.components_.shape[0]return X.dot(self.components_)def __repr__(self):return "PCA(n_components=%d)" % self.n_components使用
生成数据
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)
使用
from playML.PCA import PCApca = PCA(n_components=2)
pca.fit(X)
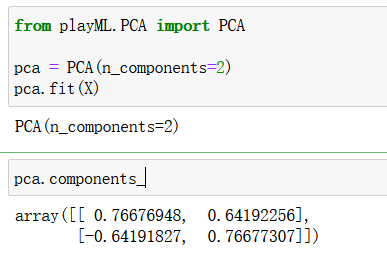
pca = PCA(n_components=1)
pca.fit(X)
降维
X_reduction = pca.transform(X)
X_reduction.shape
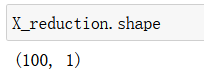
恢复降维
X_restore = pca.inverse_transform(X_reduction)
X_restore.shape
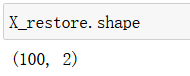
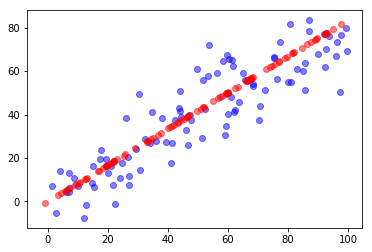
可视化
plt.scatter(X[:,0], X[:,1], color='b', alpha=0.5)
plt.scatter(X_restore[:,0], X_restore[:,1], color='r', alpha=0.5)
plt.show()
scikit-learn中的PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(X)
pca.components_
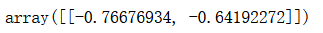
X_reduction = pca.transform(X)
X_restore = pca.inverse_transform(X_reduction)
plt.scatter(X[:,0], X[:,1], color='b', alpha=0.5)
plt.scatter(X_restore[:,0], X_restore[:,1], color='r', alpha=0.5)
plt.show()
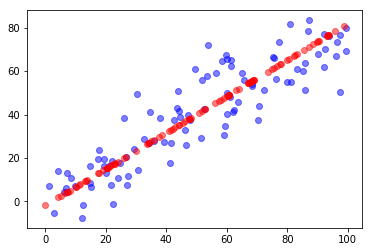
真实数据测试
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
digits = datasets.load_digits()
X = digits.data
y = digits.target
分数据集
from sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
训练
from sklearn.neighbors import KNeighborsClassifierknn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
knn_clf.score(X_test, y_test)
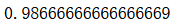
PCA降维
from sklearn.decomposition import PCApca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
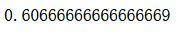
速度提高了 精度降低了
主成分所解释的方差
pca.explained_variance_ratio_
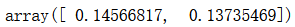
from sklearn.decomposition import PCApca = PCA(n_components=X_train.shape[1])
pca.fit(X_train)
pca.explained_variance_ratio_

可视化
plt.plot([i for i in range(X_train.shape[1])], [np.sum(pca.explained_variance_ratio_[:i+1]) for i in range(X_train.shape[1])])
plt.show()
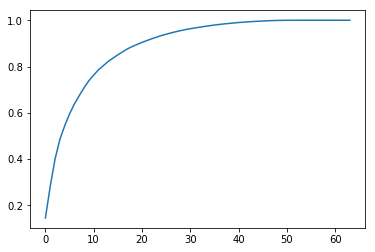
主成分个数可解释95%+的方差
pca = PCA(0.95)
pca.fit(X_train)
pca.n_components_
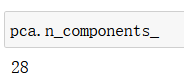
说明需要28维
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
knn_clf.score(X_test_reduction, y_test)
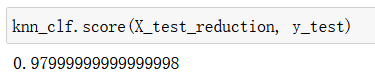
使用PCA对数据进行降维可视化
pca = PCA(n_components=2)
pca.fit(X)
X_reduction = pca.transform(X)
for i in range(10):plt.scatter(X_reduction[y==i,0], X_reduction[y==i,1], alpha=0.8)
plt.show()

MNIST手写数据集 训练
import numpy as np from sklearn.datasets import fetch_openmlmnist = fetch_openml('mnist_784')X, y = mnist['data'], mnist['target']
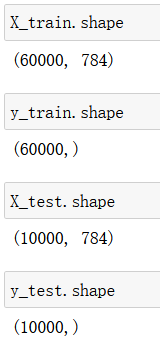
X_train = np.array(X[:60000], dtype=float)
y_train = np.array(y[:60000], dtype=float)
X_test = np.array(X[60000:], dtype=float)
y_test = np.array(y[60000:], dtype=float)
使用KNN
from sklearn.neighbors import KNeighborsClassifierknn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
%time knn_clf.score(X_test, y_test)

PCA进行降维
from sklearn.decomposition import PCA
pca = PCA(0.90)
pca.fit(X_train)
X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)
X_train_reduction.shape
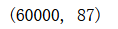
knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)
%time knn_clf.score(X_test_reduction, y_test)

使用PCA降噪
例子
import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 5, size=100)
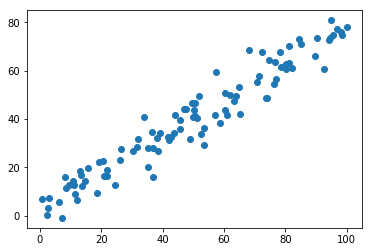
plt.scatter(X[:,0], X[:,1])
plt.show()
from sklearn.decomposition import PCApca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.transform(X)
X_restore = pca.inverse_transform(X_reduction)
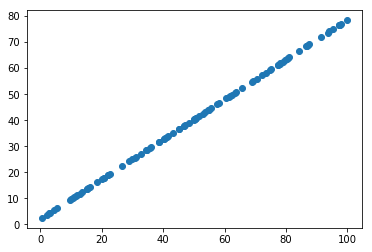
plt.scatter(X_restore[:,0], X_restore[:,1])
plt.show()
手写识别例子
from sklearn import datasetsdigits = datasets.load_digits()
X = digits.data
y = digits.target
制造噪音
noisy_digits = X + np.random.normal(0, 4, size=X.shape)
取100个
example_digits = noisy_digits[y==0,:][:10]
for num in range(1,10):example_digits = np.vstack([example_digits, noisy_digits[y==num,:][:10]])
绘制
def plot_digits(data):fig, axes = plt.subplots(10, 10, figsize=(10, 10),subplot_kw={'xticks':[], 'yticks':[]},gridspec_kw=dict(hspace=0.1, wspace=0.1)) for i, ax in enumerate(axes.flat):ax.imshow(data[i].reshape(8, 8),cmap='binary', interpolation='nearest',clim=(0, 16))plt.show()plot_digits(example_digits)

降噪
pca = PCA(0.5).fit(noisy_digits)
pca.n_components_
components = pca.transform(example_digits)
filtered_digits = pca.inverse_transform(components)
plot_digits(filtered_digits)

特征脸
加载数据
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people()
查看属性
faces.keys()
faces.data.shape
faces.target_names
faces.images.shape

获取36个数据
random_indexes = np.random.permutation(len(faces.data))
X = faces.data[random_indexes]
example_faces = X[:36,:]
example_faces.shape
绘制
def plot_faces(faces):fig, axes = plt.subplots(6, 6, figsize=(10, 10),subplot_kw={'xticks':[], 'yticks':[]},gridspec_kw=dict(hspace=0.1, wspace=0.1)) for i, ax in enumerate(axes.flat):ax.imshow(faces[i].reshape(62, 47), cmap='bone')plt.show()plot_faces(example_faces)

特征脸
%%time
from sklearn.decomposition import PCA
pca = PCA(svd_solver='randomized')# 随机方式
pca.fit(X)
pca.components_.shape
绘制
plot_faces(pca.components_[:36,:])