SPSS基础操作：对数据按照样本观测值进行排序-编程知识

在整理数据资料或者查看分析结果时，我们通常希望样本观测值能够按照某一变量的大小进行升序或者降序排列，比如我们想按照学生的学习成绩进行排序，按照销售额的大小对各个便利店进行排序等。以本章附带的数据4为例，如果要按照y4体重变量进行降序排列，操作步骤如下：

图4.88显示了按照y4体重变量排序之前的数据。

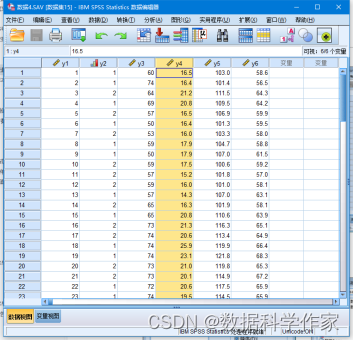
在菜单栏中选择“数据”→“个案排序”命令，如图4.89所示。

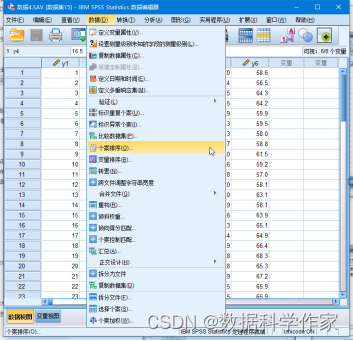
系统将会弹出“个案排序”对话框，在该对话框中选择“体重”变量，并单击按钮，将其选入“排序依据”列表框。然后在“排列顺序”组合框中选中“降序”选项，如图4.90所示。

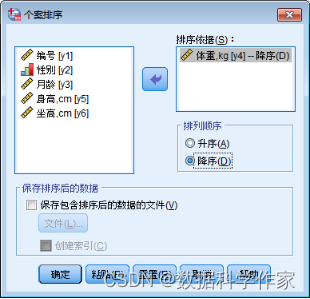
设置后，在“个案排序”对话框下方可以选择是否保存排序后的数据。如果需要进行保存，就选中“保存包含排序后的数据的文件”复选框，然后下方的“文件”按钮将会被激活。单击“文件”按钮，即可弹出如图4.91所示的“将排序后的数据另存为”对话框，用户可以在该对话框中设置文件路径，对数据进行保存。

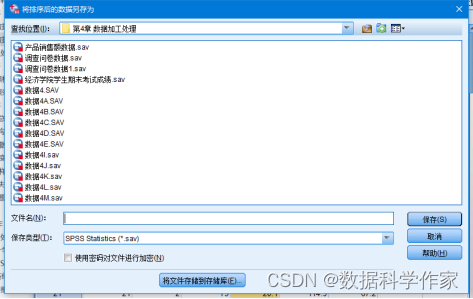
以上内容节选自《SPSS统计学基础与实证研究应用精解》张甜杨维忠清华大学出版社 2023年。为使用SPSS写作实证研究类论文所精心设计，实现零基础入门学会用SPSS写论文的目的。

这儿我谈谈SPSS学习的分析。针对没有统计学基础的新手和小白，SPSS入门方面，建议一定边看书边操作，通过边学知识边上手操作的方式学习，会事半功倍，也有解决问题的成就感。推荐三本避雷避坑、亲测可行的网红图书，也是杨维忠、张甜老师撰写的SPSS三部曲：

1、《SPSS统计分析入门与应用精解(视频教学版)》杨维忠张甜清华大学出版社 2022年。侧重SPSS统计分析操作，体现在对于窗口选项设置和运行结果解读都非常全面、细致、到位；

2、《SPSS统计学基础与实证研究应用精解》张甜杨维忠清华大学出版社 2023年。为使用SPSS写作实证研究类论文所精心设计，实现零基础入门学会用SPSS写论文的目的。

3、《SPSS统计分析商用建模与综合案例精解》杨维忠张甜清华大学出版社 2021年。侧重使用SPSS开展数据挖掘、机器学习以及统计分析的综合应用。

《SPSS统计分析入门与应用精解（视频教学版）》杨维忠 张甜编著清华大学出版社。这是一本精解SPSS统计分析基础入门与应用的教材，山东大学陈强教授作序推荐，通过“精解统计分析原理、精解SPSS窗口选项设置、精解SPSS输出结果”三要素，帮助读者真正掌握常用统计分析软件SPSS的应用。适用于经济金融、管理、市场营销、教育学、心理学、医学等各类专业。

全书共14章。第1章为SPSS基础与应用操作概述；第2~7章介绍SPSS的基本统计分析方法，包括描述统计分析方法、比较平均值分析方法、非参数检验方法、相关分析方法、一般线性模型、各类常用回归分析方法等；第8~13章介绍SPSS的常用高级统计分析方法，包括时间序列预测方法、聚类分析方法、决策树分析与判别分析方法、生存分析方法、降维分析方法等；第14章为如何使用SPSS进行高质量综合性研究。每章有教学重点提示，章后有“知识点总结与练习题”，帮助读者增强学习效果，形成了“从基础原理到操作精解，从数据分析到案例应用”的完整教学闭环。与本书配套的还有教学PPT和作者新讲解的全套视频资料以辅助教学，力求实现最佳教学效果。

本书可作为经济学、管理学、统计学、金融学、社会学、医学、电子商务等相关专业的在校本、专科大学生及研究生学习、应用SPSS的主要教材，还可作为职场人士掌握SPSS应用、提升数据分析能力，进而提升工作效率、改善绩效水平的工具书。

如果是写论文使用SPSS，则推荐《SPSS统计学基础与实证研究应用精解》张甜杨维忠著清华大学出版社

《SPSS统计学基础与实证研究应用精解》张甜杨维忠著清华大学出版社

本书手把手教会使用SPSS撰写实证研究类论文或开展数据分析

常用统计学原理、实证研究的套路、调查问卷设计、信度分析、效度分析、T检验、ANOVA分析、相关性分析、回归分析、中介效应、调节效应、因子分析、聚类分析……一应俱全。

如果是使用SPSS开展数据挖掘、机器学习以及统计分析的综合应用，推荐《SPSS统计分析商用建模与综合案例精解》杨维忠张甜编著清华大学出版社 2021年。国内众多高校作为核心专业课程教材。在51CTO举办的“2021年度最受读者喜爱的IT图书作者评选”中，《SPSS统计分析商用建模与综合案例精解》荣获“数据科学领域最受读者喜爱的图书TOP5”。