1049. 最后一块石头的重量 II

题目
文章讲解
视频讲解

思路：dp[j] 表示容量为 j 的背包，最多可以背最大重量为dp[j]。

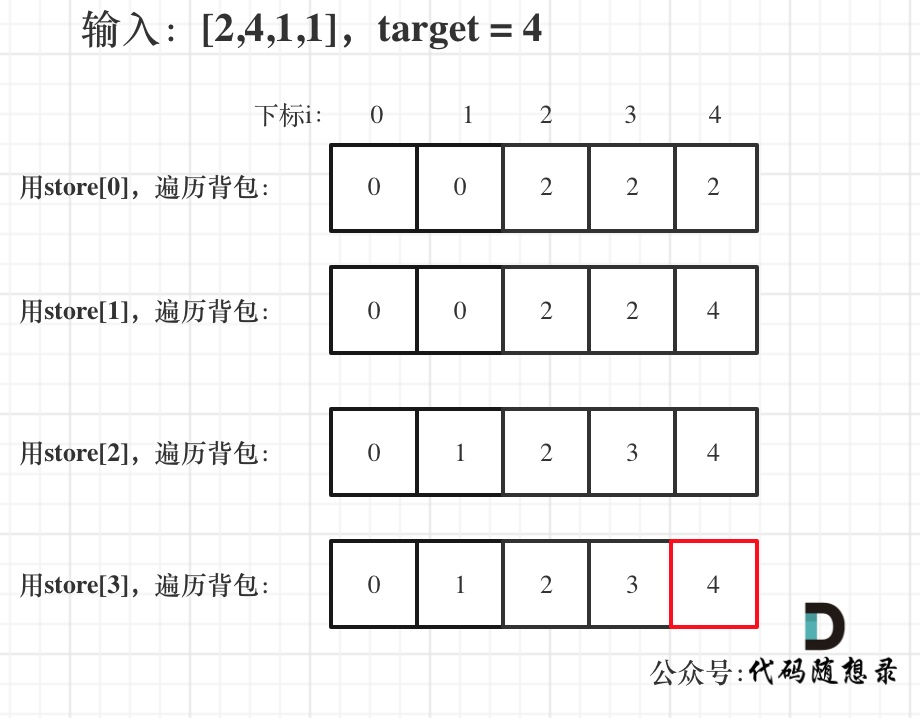
class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int i = 0; i < stones.length; i++) {sum += stones[i];}int target = sum / 2;int[] dp = new int[target + 1];for (int i = 0; i < stones.length; i++) {//物品大小for (int j = target; j >= stones[i]; j--) {//背包容量dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}

494. 目标和

题目
文章讲解
视频讲解

思路：将集合分为正数和负数两组。

1. dp[j] 表示填满 j（包括j）这么大容积的包，有dp[j]种方法。
2. 递推公式：dp[j]=dp[j-nums[i]]
3. 初始化dp[0]=1(填满 0 这么大容积的包，有 1 种方法)
4. 遍历顺序：先遍历物品，后倒序遍历背包

class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int i : nums)sum += i;if (target < 0 && sum < -target)return 0;int size = (sum + target) / 2;if ((sum + target) % 2 != 0)return 0;int[] dp = new int[size + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = size; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[size];}
}

474.一和零

题目
文章讲解
视频讲解

思路：

1. dp[i][j]表示i个0和j个1时的最大物品数
2. 递推公式：dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] +1）扣除物品中0，1数量，将物品数加1
3. 初始化：倒序遍历取max，为了保证不被覆盖都设置为0即可
4. for循环遍历背包容量且从后向前遍历

注意：此题是0-1背包问题，m n不是包含了两种物品，m 和 n相当于是一个背包，两个维度的背包。本题中strs 数组里的元素就是物品，每个物品都是一个！

class Solution {public int findMaxForm(String[] strs, int m, int n) {// dp[i][j]表示i个0和j个1时的最大子集int[][] dp = new int[m + 1][n + 1];int oneNum, zeroNum;for (String str : strs) {oneNum = 0;zeroNum = 0;for (char ch : str.toCharArray()) {if (ch == '0')zeroNum++;elseoneNum++;}// 倒序遍历for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
}