模拟堆
- 1.题目
- 2.基本思想
- 3.代码实现
1.题目
维护一个集合,初始时集合为空,支持如下几种操作:
I x,插入一个数 x;PM,输出当前集合中的最小值;DM,删除当前集合中的最小值(数据保证此时的最小值唯一);D k,删除第 k 个插入的数;C k x,修改第 k 个插入的数,将其变为 x;
现在要进行 N次操作,对于所有第 2 个操作,输出当前集合的最小值。
输入格式
第一行包含整数 N N N。
接下来 N N N 行,每行包含一个操作指令,操作指令为 I x,PM,DM,D k 或 C k x 中的一种。
输出格式
对于每个输出指令 PM,输出一个结果,表示当前集合中的最小值。
每个结果占一行。
数据范围
1 ≤ N ≤ 1 0 5 1≤N≤10^5 1≤N≤105
− 1 0 9 ≤ x ≤ 1 0 9 −10^9≤x≤10^9 −109≤x≤109
数据保证合法。 数据保证合法。 数据保证合法。
输入样例:
8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM
输出样例:
-10
6
2.基本思想
3.代码实现
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.nio.Buffer;
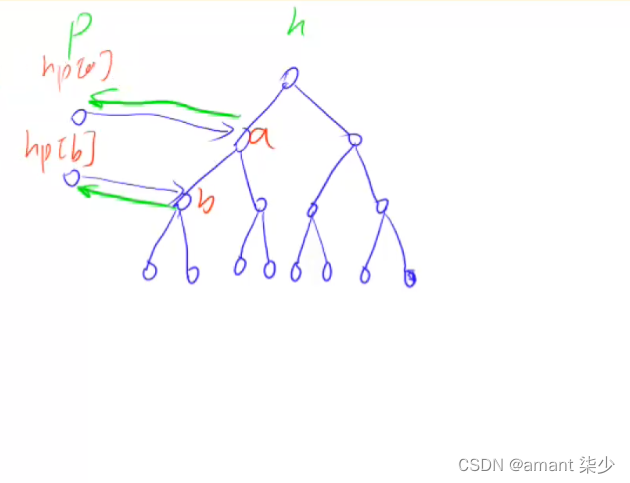
import java.util.Scanner;public class _839模拟堆 {static int N = 100010;static int[] h = new int[N];//h代表heap(堆)static int[] ph = new int[N];//ph(point->heap)可以获得第几个插入的元素现在在堆的那个位置static int[] hp = new int[N]; //hp(heap->point)可以获得在堆的第n个元素存的是第几个插入的元素static int size, m;static void heap_swap(int a, int b) {//交换在heap中位置分别为a,b的两个元素swap(ph, hp[a], hp[b]);//第一步交换蓝色线swap(hp, a, b);//绿线swap(h, a, b);//真实值}static private void swap(int[] arr, int a, int b) {int temp = arr[a];arr[a] = arr[b];arr[b] = temp;}private static void down(int u) {//当前堆的元素下沉int min = u;if (u * 2 <= size && h[u * 2] < h[min]) min = u * 2;if (u * 2 + 1 <= size && h[u * 2 + 1] < h[min]) min = u * 2 + 1;if (u != min) {heap_swap(min, u);down(min);}}private static void up(int u) {while (u / 2 > 0 && h[u / 2] > h[u]) {heap_swap(u / 2, u);u /= 2;}}public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));int n = Integer.parseInt(br.readLine());while (n-- > 0) {String[] s = br.readLine().split(" ");String opt = s[0];if (opt.equals("I")) {int x = Integer.parseInt(s[1]);size++;m++;h[size] = x;ph[m] = size;hp[size] = m;up(size);} else if (opt.equals("PM")) System.out.println(h[1]);else if (opt.equals("DM")) {heap_swap(1, size);size--;down(1);} else if (opt.equals("D")) {int k = Integer.parseInt(s[1]);int u = ph[k];heap_swap(u, size);size--;down(u);up(u);} else if (opt.equals("C")) {int k = Integer.parseInt(s[1]);int x = Integer.parseInt(s[2]);int u = ph[k];h[u] = x;down(u);up(u);}}}
}![[2-远程开发-01]idea远程连接开发](https://img-blog.csdnimg.cn/direct/f310ddc9d58d4455b6dc0fe6911d3327.png)