让我们来几道高中的组合题吧:

1.我们一定有n个向下,为
2.我们挑最大的两个,条件是他们奇偶性相同,为2*A10,2;
3.用捆绑法即可。

4.我们用隔板法,为
5.问题等价于23个相同的球放到3个盒子里,每个盒子至少有一个。
下面我们直接看题:

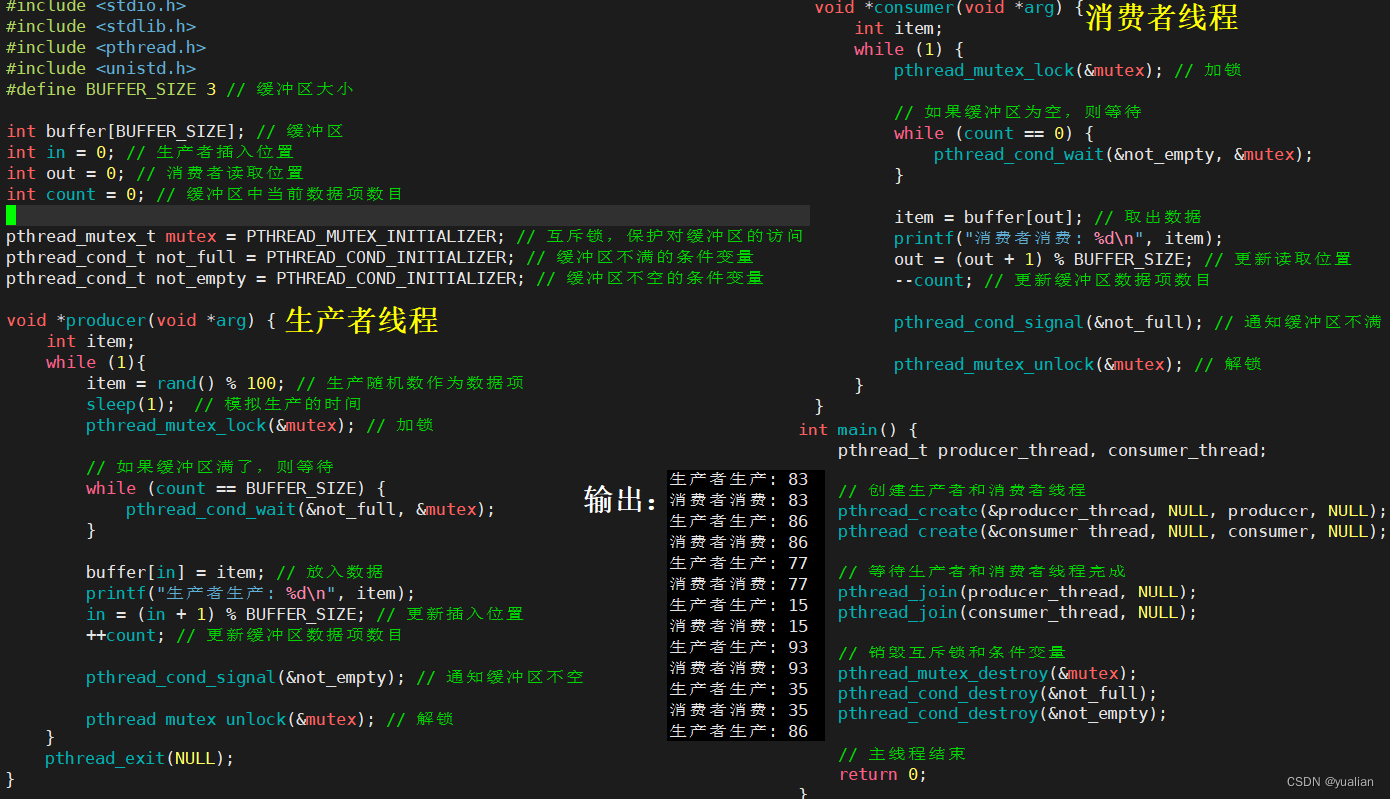
很显然,当无限制条件时,每个a[i]贡献1+2+...+n,因此我们对没有限制的快速幂,有限制的单独计算即可,下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,k,mod=1e9+7,x,y,ck;
map<int,int> mp;
struct node{int x,y;
}a[100010];
bool cmp(node a,node b){if(a.x==b.x) return a.y<b.y;else return a.x<b.x;
}
long long quicks(long long a,long long b){long long i=1;while(b){if(b&1) i=(a*i)%mod;b>>=1;a=(a*a)%mod;}return i;
}
signed main(){cin>>n>>m>>k;if(n%2==0) ck=n/2*(n+1)%mod;else ck=n*((n+1)/2)%mod;for(int i=1;i<=k;i++){scanf("%d%d",&a[i].x,&a[i].y);}sort(a+1,a+k+1,cmp);for(int i=1;i<=k;i++){if(a[i+1].x==a[i].x&&a[i+1].y==a[i].y) continue;if(mp.count(a[i].x)==0) mp[a[i].x]=(ck-a[i].y+mod)%mod;else mp[a[i].x]=(mp[a[i].x]-a[i].y+mod)%mod;}int ans=quicks(ck,m-mp.size());map<int,int>::iterator it=mp.begin();for(;it!=mp.end();it++){ans=(ans*(it->second)+mod)%mod;}cout<<ans;
}接题:

没有障碍时,就是求n个数的排列,而我们现在相当于限制了每一行不能放的元素(互不相同)。
因此,我们可以吧问题等价于1----n个格子,每一个格子不能放与自己下标相同的元素。
这样子就是一个错排问题:
下面给出错排的求解思路:

下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,x,a[205];
long long f(long long n){if(a[n]!=-1) return a[n];else return a[n]=(n-1)*(f(n-1)+f(n-2));
}
signed main(){cin>>n;memset(a,-1,sizeof(a));a[1]=0;a[2]=1;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){scanf("%d",&x);}}if(n<=1) cout<<0;else{ cout<<f(n);}
}下面看看经典的卡特兰数:
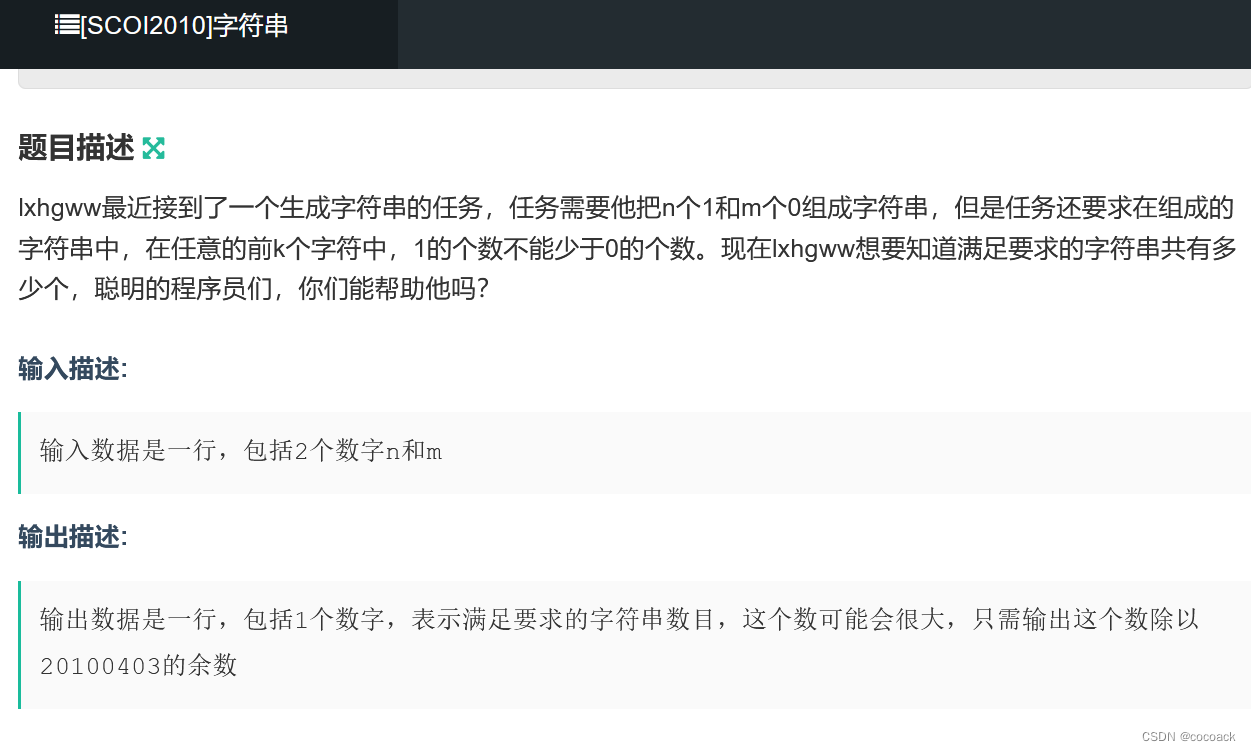

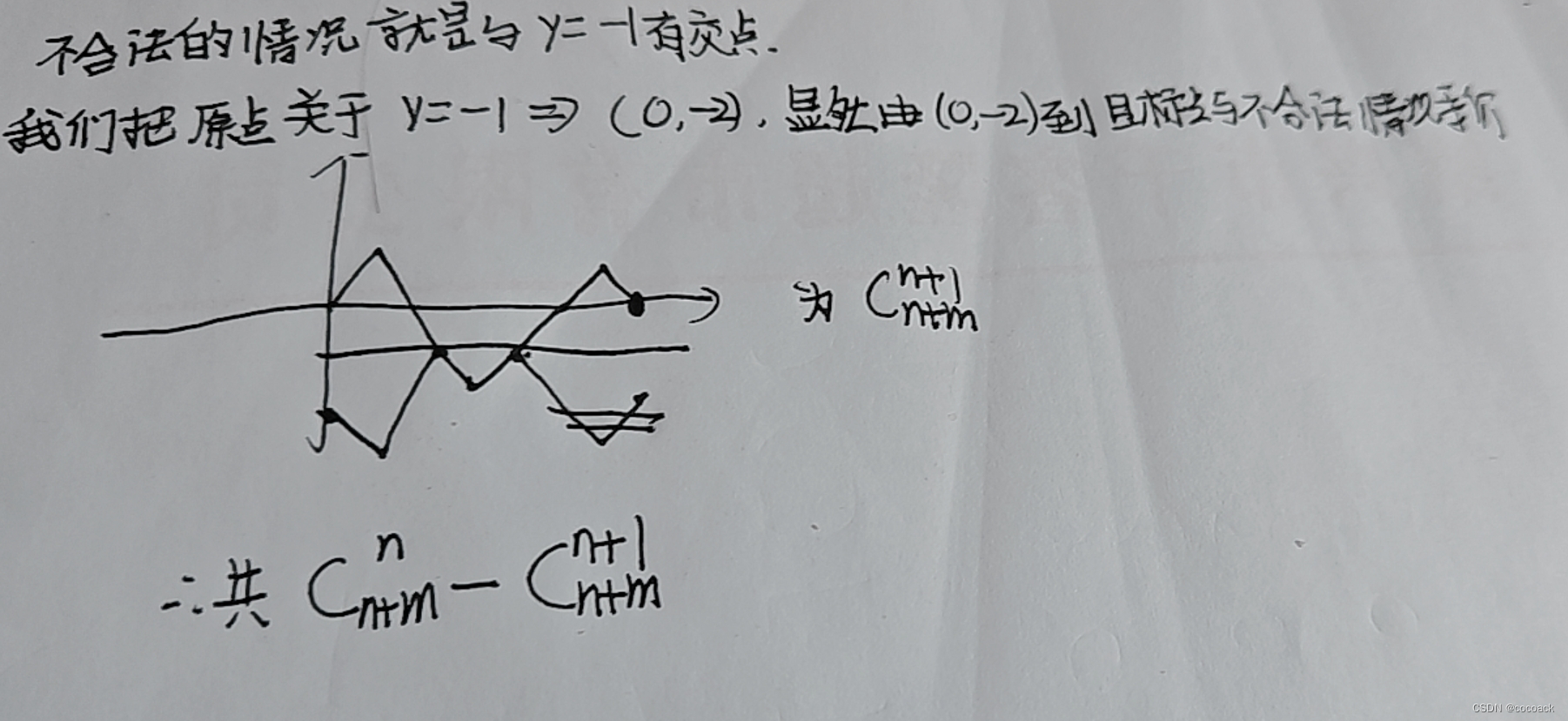
(!!!只有第一段翻折)
组合数的除我们用费马小定理求逆元即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,mod;
int pow1(int a,int b){int i=1;while(b){if(b&1) i=i*a%mod;b>>=1;a=a*a%mod;}return i;
}
signed main(){cin>>n>>m;mod=20100403;int ret=n+1-m;for(int i=n+1;i<=n+m;i++) ret=ret*i%mod;int ck=n+1;for(int i=1;i<=m;i++) ck=ck*i%mod;ck=pow1(ck,mod-2);cout<<ck*ret%mod;
}