1. 并查集原理

在一些情况下，需要将 n 个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于哪个集合的运算。适合于描述这类问题的抽象数据类型称为并查集。

给大家举个例子：我在武汉上大学，但是我家在襄阳，每次来武汉上学的时候都需要坐高铁。在我第一次来学校的时候，是我一个人坐高铁来的，此时我就可以看成是一个单元素集合，但是到了大学之后，我认识了一些新朋友，并且我发现他们有的是襄阳的，有的是孝感的，有的就是武汉本地的，所以我们就约好了寒假来的时候襄阳的和襄阳的一起坐高铁过来，孝感的和孝感的，武汉的和武汉的一起来学校，这时候我们这几个人就组成了一个具有一定相同点的集合。

我用下面的图表示我和我的朋友们：

在上大学之前，我们都是单元素的集合，所以都用 -1 表示，我用 0 来表示，我的另外几个襄阳的朋友分别是 1、4、6，孝感的朋友是 2、5、8，武汉的朋友就是3、7、9，所以通过图形来表示的话就是：

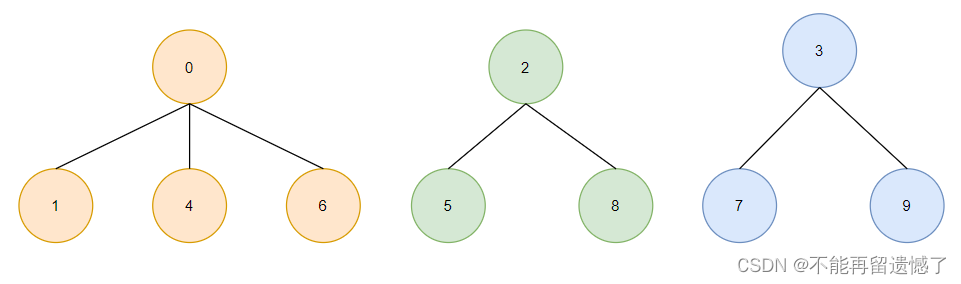
在上面的树林中，每一棵树表示一个集合，这是使用树林给大家显示出来的关系，可以对于上面的数组，我们应该如何表现出这种关系呢？

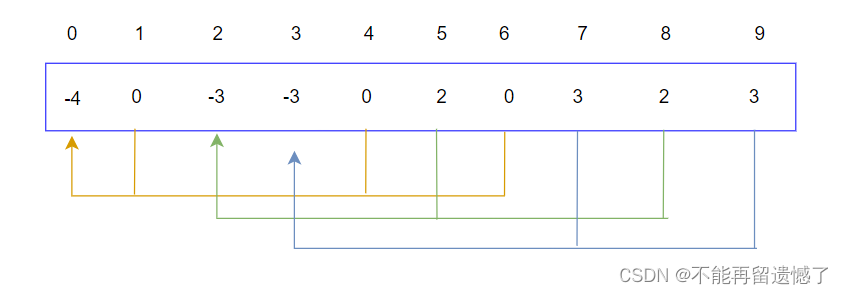
• 数组的下标对应集合中元素的编号
• 数组中如果为负数，负号表示根，数字代表该集合中元素的个数
• 数组中如果为非负数，代表该元素双亲在数组中的下标

从襄阳到武汉会经过孝感，所以我们襄阳的朋友和孝感的朋友约定到了孝感之后一起去学校，那么襄阳表示的集合就会和孝感表示的集合进行合并：

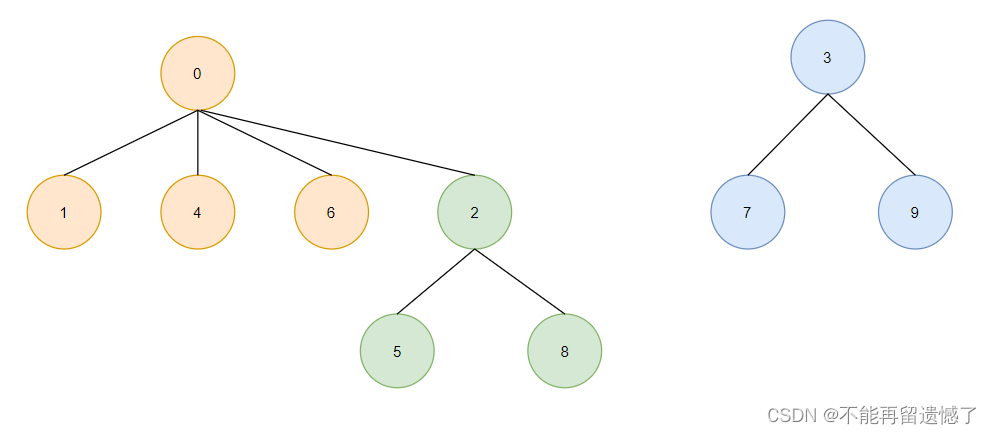
这样的话，我们数组对应下标的值也需要改变：

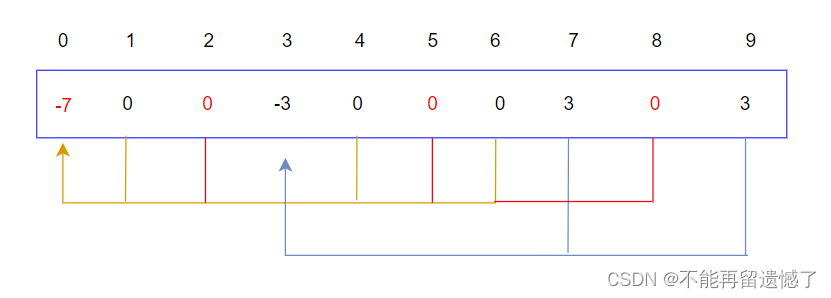
现在 0 集合中有 7 个元素，所以 -4 就要改为 -7，而 2 集合因为合并到了 0 集合，所以原来的根在数组中所表示的值就要改为 0，其他 2 集合的元素的根在数组中所表示的值也要改为 0。

通过上面的例子，我们可以知道并查集可以解决下面问题：

1. 查找元素属于哪个集合

• 沿着数组表示的树形结构往上一直找到根（树中元素为负数的位置）

2. 查看两个元素是否属于同一个集合

• 分别沿着数组表示的树形结构往上一直找到根，如果根相同，则表示在同一个集合中，不相同则表示不在同一个集合中

3. 将两个不相同的集合归并为一个集合
4. 求集合的个数

• 遍历数组，数组中元素的值为负数的个数即为集合的个数

2. 并查集的实现

接下来，我们将学习如何实现并查集：

public class UnionFindSet {private int[] elem; //并查集的底层是一个数组public UnionFindSet(int n) {this.elem = new int[n]; //根据数据的多少创建适合大小的数组Arrays.fill(elem, -1); //开始的时候每个元素都是单元素的集合，所以我们数组每个元素的默认值都设置为-1}/*** 查找数据 x 的根节点下标* @param x* @return*/public int findRoot(int x) {if (x < 0) throw new ArrayIndexOutOfBoundsException("下标为负数，不合法");while (elem[x] >= 0) {x = elem[x];}return x;}/*** 判断x1和x2是否位于同一个集合* @param x1* @param x2* @return*/public boolean isSameUnionFindSet(int x1, int x2) {if (x1 < 0 || x2 < 0) throw new ArrayIndexOutOfBoundsException("下标为负数，不合法");int index1 = findRoot(x1);int index2 = findRoot(x2);//当x1的根节点和x2的根节点相同且不为-1的时候表明是一个集合if (index1 == index2 && index1 != -1) return true;return false;}/*** 将两个集合合并为一个集合* @param x1* @param x2*/public void union(int x1, int x2) {int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1 == index2) return;elem[index1] = elem[index1] + elem[index2];elem[index2] = index1;}public int getCount() {int count = 0;for (int x : elem) {if (x < 0) count++;}return count;}
}

3. 并查集运用

3.1 省份数量

https://leetcode.cn/problems/number-of-provinces/

3.1.1 题目要求

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

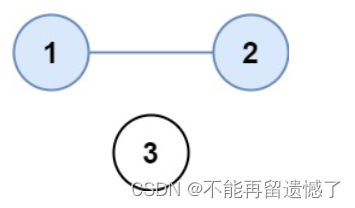
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

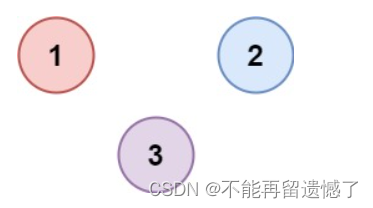
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

1 <= n <= 200
n == isConnected.length
n == isConnected[i].length
isConnected[i][j] 为 1 或 0
isConnected[i][i] == 1
isConnected[i][j] == isConnected[j][i]

3.1.2 做题思路

首先我们可以先遍历数组，遇到为 1 的位置，就说明 i 城市和 j 城市相连，那么我们就可以将这两个单元素的集合合并到一个元素，后面再遍历到 1 的时候，使用相同的操作进行集合的归并，这样最后直接相连和间接相连的城市就会在一个集合中。

3.1.3 代码实现

class Solution {public int findCircleNum(int[][] isConnected) {int len = isConnected.length;UnionFindSet ufs = new UnionFindSet(len);for (int i = 0; i < len; i++) {for (int j = 0; j < isConnected[0].length; j++) {if (isConnected[i][j] == 1) {ufs.union(i, j);}}}return ufs.getCount();}
}class UnionFindSet {private int[] elem; //并查集的底层是一个数组public UnionFindSet(int n) {this.elem = new int[n]; //根据数据的多少创建适合大小的数组Arrays.fill(elem, -1); //开始的时候每个元素都是单元素的集合，所以我们数组每个元素的默认值都设置为-1}/*** 查找数据 x 的根节点下标* @param x* @return*/public int findRoot(int x) {if (x < 0) throw new ArrayIndexOutOfBoundsException("下标为负数，不合法");while (elem[x] >= 0) {x = elem[x];}return x;}/*** 判断x1和x2是否位于同一个集合* @param x1* @param x2* @return*/public boolean isSameUnionFindSet(int x1, int x2) {if (x1 < 0 || x2 < 0) throw new ArrayIndexOutOfBoundsException("下标为负数，不合法");int index1 = findRoot(x1);int index2 = findRoot(x2);//当x1的根节点和x2的根节点相同且不为-1的时候表明是一个集合if (index1 == index2 && index1 != -1) return true;return false;}/*** 将两个集合合并为一个集合* @param x1* @param x2*/public void union(int x1, int x2) {int index1 = findRoot(x1);int index2 = findRoot(x2);if (index1 == index2) return;elem[index1] = elem[index1] + elem[index2];elem[index2] = index1;}public int getCount() {int count = 0;for (int x : elem) {if (x < 0) count++;}return count;}
}

3.2 等式方程的可满足性

https://leetcode.cn/problems/satisfiability-of-equality-equations/description/

3.2.1 题目要求

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：“a==b” 或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。

示例 1：

输入：["a==b","b!=a"]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个			方程。没有办法分配变量同时满足这两个方程。

示例 2：

输入：["b==a","a==b"]
输出：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。

示例 3：

输入：["a==b","b==c","a==c"]
输出：true

示例 4：

输入：["a==b","b!=c","c==a"]
输出：false

示例 5：

输入：["c==c","b==d","x!=z"]
输出：true

提示：

1 <= equations.length <= 500
equations[i].length == 4
equations[i][0] 和 equations[i][3] 是小写字母
equations[i][1] 要么是 '='，要么是 '!'
equations[i][2] 是 '='

3.2.2 做题思路

因为这道题目只有 == 和 != 关系，所以我们可以先遍历一遍数组，当字符串的 1 下标为 = 的时候，就说明是相等关系，我们就将这个字符串的 0 位置和 3 位置的数字给添加到一个集合中，这样，遍历一次之后，我们就可以把所有相同的数字给归并到一个集合中。然后我们再遍历一遍数组，这次当字符串的 1 下标为 ! 的时候，就说明是不等关系，那么我们只需要判断这两个元素是否在同一个集合中就可以了，如果在同一个集合中，就说明不符合，返回 false。

3.2.3 代码实现

class Solution {public boolean equationsPossible(String[] equations) {UnionFindSet ufs = new UnionFindSet(26);for (String s : equations) {if (s.charAt(1) == '=') {ufs.union(s.charAt(0) - 'a', s.charAt(3) - 'a');}}for (String s : equations) {if (s.charAt(1) == '!') {boolean flg = ufs.isSameUnionFindSet(s.charAt(0) - 'a', s.charAt(3) - 'a');if (flg) return false;}}return true;}
}