Visual Studio 2010+C#实现信源编码-编程知识

1. 要求

本文设计了一套界面系统，该系统能够实现以下功能：

克劳夫特不等式的计算，并且能够根据计算结果给出相应的信息。
可通过用户输入的初始条件然后给出哈夫曼编码以及LZ编码，结果均通过对话框来显示
哈夫曼编码结果包含相应的码字，信源熵，平均码长以及编码效率
LZ编码结果的形式如下图所示，包括每一个短语，段号，码字以及二进制码

2.过程

1.界面总体设计：

初始界面包含用户登录，克劳夫特不等式，哈夫曼编码以及LZ编码四个模块，每一个模块都用groupbox控件来单独设计，使得整个系统看起来更加合理清晰

图1 初始界面

2.每一个部分的设计过程：

（1）登录

private void button1_Click(object sender, EventArgs e){string result=textBox1.Text +" 你好!欢迎使用信源编码程序";Form2 mfrm = new Form2(result);mfrm.ShowDialog();}

图2 用户登录

点击登录后弹出出的对话框设计

public partial class Form2 : Form{private string message;public Form2(string msg){InitializeComponent();message = msg;}private void Form2_Load(object sender, EventArgs e){label1.Text = message;}private void button1_Click(object sender, EventArgs e){this.Close();}}

图3 登录后弹出的对话框

（2）克劳夫特不等式（对话框设计与图3一致）

private void button2_Click(object sender, EventArgs e){Double m;String a;m = Convert.ToDouble(textBox2.Text);int k;double[] y = new double[richTextBox1.Lines.Length];double sum = 0;for (int i = 0; i < richTextBox1.Lines.Length; i++){a = richTextBox1.Lines[i];k =a.Length;sum += Math.Pow(m, -k);}if (sum <= 1){       Form2 mfrm = new Form2(Convert.ToString(sum) + "<=1,满足克劳夫特不等式，存在唯一可译码");mfrm.Show();}else{Form2 mfrm = new Form2(Convert.ToString(sum) + ">1,不满足克劳夫特不等式，不存在唯一可译码");mfrm.Show();}

图4 克劳夫特不等式模块

（3）哈夫曼编码（重点）

定义类：

public class Node                                 //哈夫曼树结点{public string code;public double prioirry;                           //保存权值public Node lchild;                           //左孩子指针public Node rchild;                           //右孩子指针}

定义字典存储结果：

private Dictionary<string, string> dictcode = new Dictionary<string, string>(); //结果字典

比较函数：

public int comparisonNode(Node n1, Node n2){return (int)(100*n1.prioirry -100*(n2.prioirry ));}

遍历哈夫曼树的函数：

private void viewTree(Node n, string v){if ( n.code !=null){dictcode.Add(n.code, v);}else{if (n.lchild != null){string vl = v + "1";viewTree(n.lchild, vl);}if (n.rchild != null){string vr = v + "0";viewTree(n.rchild, vr);}}}

编码函数：

private string encode(double[] p){dictcode.Clear();Dictionary<string, double> priorityQueue = new Dictionary<string, double>();for (int i = 0; i < p.Length; i++){string ci ="x"+ Convert.ToString(i); priorityQueue.Add(ci, p[i]);}List<Node> listpc = new List<Node>();foreach (var item in priorityQueue){listpc.Add(new Node() { prioirry = item.Value, lchild = null, rchild = null,code = item.Key });}listpc.Sort(comparisonNode);while (listpc.Count > 1){Node n = new Node();n.prioirry = listpc[0].prioirry + listpc[1].prioirry;n.lchild = listpc[0];n.rchild = listpc[1];listpc.RemoveAt(0);listpc.RemoveAt(0);int index = -1;for (int i = 0; i < listpc.Count; i++){if (n.prioirry <= listpc[i].prioirry){index = i;break;}}if (index == -1){ index = listpc.Count; }listpc.Insert(index, n);}string encodestr = "";viewTree(listpc[0], "");for (int i = 0; i < p.Length; i++){encodestr += dictcode["x"+Convert.ToString(i)]+' ';}return encodestr;}

编码按钮中代码：

private void button3_Click(object sender, EventArgs e){string[] a = new string[richTextBox2.Lines.Length];double[] px = new double[richTextBox2.Lines.Length];string[] s = new string[richTextBox2.Lines.Length];double h = 0;double k = 0;for (int i = 0; i < richTextBox2.Lines.Length; i++){a[i] = richTextBox2.Lines[i];px[i] = Convert.ToDouble(a[i]);}s =encode(px).Split(' ');for (int i = 0; i < px.Length; i++){h += -px[i] * Math.Log(px[i], 2);k += px[i] * s[i].Length;}Form3 mfrm = new Form3(encode(px),h,k,h/k);mfrm.Show();}

图5 哈夫曼编码模块

图6 哈夫曼编码结果对话框

（4）LZ编码

编码按钮中的代码：

private void button6_Click(object sender, EventArgs e){Dictionary<string, int> dic = new Dictionary<string, int>();Dictionary<char, char> xl = new Dictionary<char, char>();xl['a'] = '0';xl['b'] = '1';int len = textBox3.Text.Length;int i = 0;int n = 0;string u="";//短语string nn="";//段号string w="";//码字string k="";//二进制码string str = textBox3.Text;label5.Text = "";while (i < len){string a = Convert.ToString(str[i]);if (!dic.ContainsKey(a)){k += "(0," + xl[str[i]]+")  ";w += "(0," + str[i] + ")  ";u += str[i] + "     ";dic[a] = dic.Count + 1;i += 1;n += 1;nn += Convert.ToString(n) + "      ";}else if (i == len - 1){w +="("+Convert.ToString( dic[a]) + ", )  ";u += str[i] + "     ";n+=1;   k+="("+Convert.ToString(dic[a],2).PadLeft(Convert.ToInt16(Math.Ceiling( Math.Log(n,2))))+", )”; nn += Convert.ToString(n) + "      ";i += 1;}else{for (int j = i + 1; j < len; j++){if (!dic.ContainsKey(str.Substring(i, j + 1 - i))){n += 1;u += str.Substring(i, j - i+1) + "     ";nn += Convert.ToString(n) + "      ";w += "(" + Convert.ToString(dic[str.Substring(i, j - i)]) + ',' + str[j] + ")  ";                       k+="("+Convert.ToString(dic[str.Substring(i,j-i)],2).PadLeft(Convert.ToInt16(Math.Ceiling( Math.Log(n,2))),'0') +','+ xl[str[j]]+")  ";dic[str.Substring(i, j + 1 - i)] = dic.Count + 1;i = j + 1;break;}else if (j == len - 1){n += 1;nn += Convert.ToString(n) + "      ";u += str.Substring(i, j+1-i) + "     ";w +="("+Convert.ToString( dic[str.Substring(i, j + 1 - i)]) +", )  ";k +='(' + Convert.ToString(dic[str.Substring(i, j+1-i)], 2).PadLeft(Convert.ToInt16(Math.Ceiling(Math.Log(n, 2))), '0') + ", )  ";i = j + 1;}}}}Form4 mfrm = new Form4(u,nn,w,k);mfrm.Show();}

图7 LZ编码模块

图8 LZ编码结果对话框

设计完成

3. 测试

图9 登录测试

克劳夫特不等式：输入相应的码字之后点击按钮出现对应信息，例如下图中不等式大于1，所以可以判断不存在唯一可译码

图10 克劳夫特不等式测试

以上模块较为简单，经过验证已经可以满足要求，接下里着重对于哈夫曼以及LZ编码模块进行测试：

第一个哈夫曼测试采用书上例5-6的原题：

图11 原书例5-6

图12 哈夫曼编码测试1

对比原题与本系统计算出的结果可以发现，测试完全正确，与答案保持一致，编码效率达到了96%

第二个哈夫曼编码测试：

概率分别为 0.4，0.2，0.2，0.1，0.1

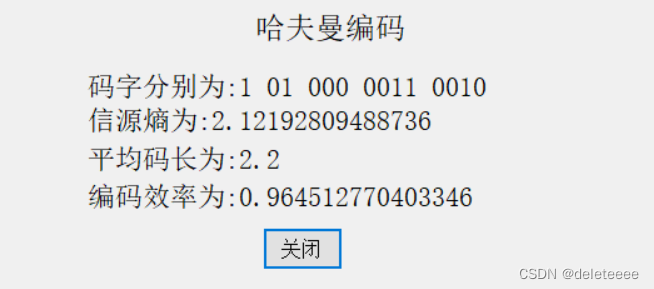
图13 哈夫曼编码测试2

通过计算可以得知该测试的结果完全正确，由此基本可以判断该模块可以成功实现哈夫曼编码，但是在计算过程中我发现如果将码字编为 00.10，11，010，011的话，虽然编码效率和图7中一样，但是此编码结果码方差为0.16，而图7中编码方差为1.36。经过分析得知，程序在编码过程中每一次概率的排序并不一定会把合并的概率放到前面，因此造成了有的信源符号被赋予更长的码。

第1个LZ编码测试：

序列（abbabaabbabbaaaaba）