对应点已知时最优变换求解介绍以及SVD代码示例-编程知识

对应点已知时最优变换求解介绍以及SVD代码示例

一、空间上两组点希望找到一个刚性变换，在最小二乘的意义上最优地对齐两个点集，就是说找到一个旋转矩阵R和一个平移向量t。

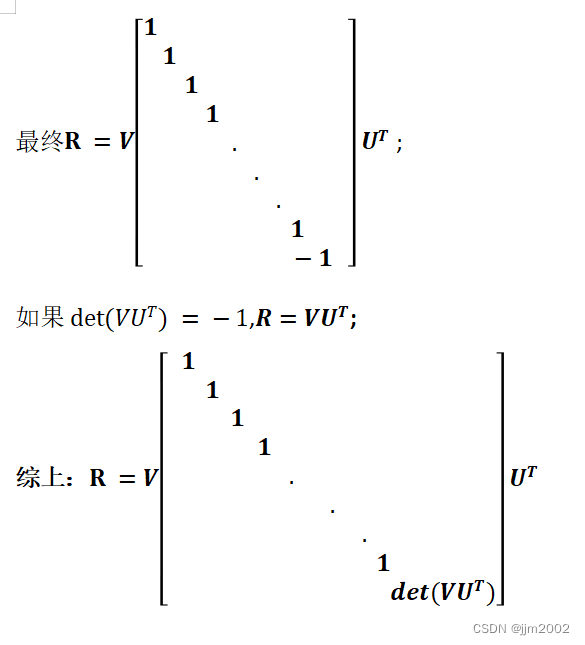
二、SVD代码示例

C++代码

#include <iostream>
#include <pcl/point_cloud.h>
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#define _USE_MATH_DEFINES
#include <math.h>
#include <pcl/common/transforms.h>
#include <pcl/registration/transformation_estimation_svd.h>using namespace Eigen;
using namespace std;int main(int argc, char** argv) {pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_in(new pcl::PointCloud<pcl::PointXYZ>());pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_out(new pcl::PointCloud<pcl::PointXYZ>());cloud_in->width = 3;cloud_in->height = 1;cloud_in->is_dense = false;cloud_in->resize(cloud_in->width * cloud_in->height);cloud_out->width = 3;cloud_out->height = 1;cloud_out->is_dense = false;cloud_out->resize(cloud_out->width * cloud_out->height);for (size_t i = 0; i < cloud_in->points.size(); i++){// RAND_MAX = 2^15 - 1cloud_in->points[i].x = 3.0f * rand() / (RAND_MAX + 1.0f);cloud_in->points[i].y = 3.0f * rand() / (RAND_MAX + 1.0f);cloud_in->points[i].z = 3.0f * rand() / (RAND_MAX + 1.0f);cout << cloud_in->points[i].x << "  \t" << cloud_in->points[i].y << "  \t" << cloud_in->points[i].z << endl;}Eigen::Affine3f transform = Eigen::Affine3f::Identity();transform.translation() << 1.0, 2.0, 3.0;float angle_x = 45 * M_PI / 180.0;float angle_y = 45 * M_PI / 180.0;float angle_z = 45 * M_PI / 180.0;transform.rotate(Eigen::AngleAxisf(angle_x, Eigen::Vector3f::UnitX()));transform.rotate(Eigen::AngleAxisf(angle_y, Eigen::Vector3f::UnitY()));transform.rotate(Eigen::AngleAxisf(angle_z, Eigen::Vector3f::UnitZ()));cout << "变换矩阵：\n" << transform.matrix() << endl;pcl::transformPointCloud(*cloud_in, *cloud_out, transform);//---------------------------------利用SVD方法求解变换矩阵--------------------------pcl::registration::TransformationEstimationSVD<pcl::PointXYZ, pcl::PointXYZ> TESVD;pcl::registration::TransformationEstimationSVD<pcl::PointXYZ, pcl::PointXYZ>::Matrix4 transformation2;TESVD.estimateRigidTransformation(*cloud_in, *cloud_out, transformation2);// -----------------------------------输出变换矩阵信息------------------------------cout << "The Estimated Rotation and translation matrices (using getTransformation function) are : \n" << endl;printf("\n");printf("    | %6.3f %6.3f %6.3f | \n", transformation2(0, 0), transformation2(0, 1), transformation2(0, 2));printf("R = | %6.3f %6.3f %6.3f | \n", transformation2(1, 0), transformation2(1, 1), transformation2(1, 2));printf("    | %6.3f %6.3f %6.3f | \n", transformation2(2, 0), transformation2(2, 1), transformation2(2, 2));printf("\n");printf("t = < %0.3f, %0.3f, %0.3f >\n", transformation2(0, 3), transformation2(1, 3), transformation2(2, 3));return 0;
}

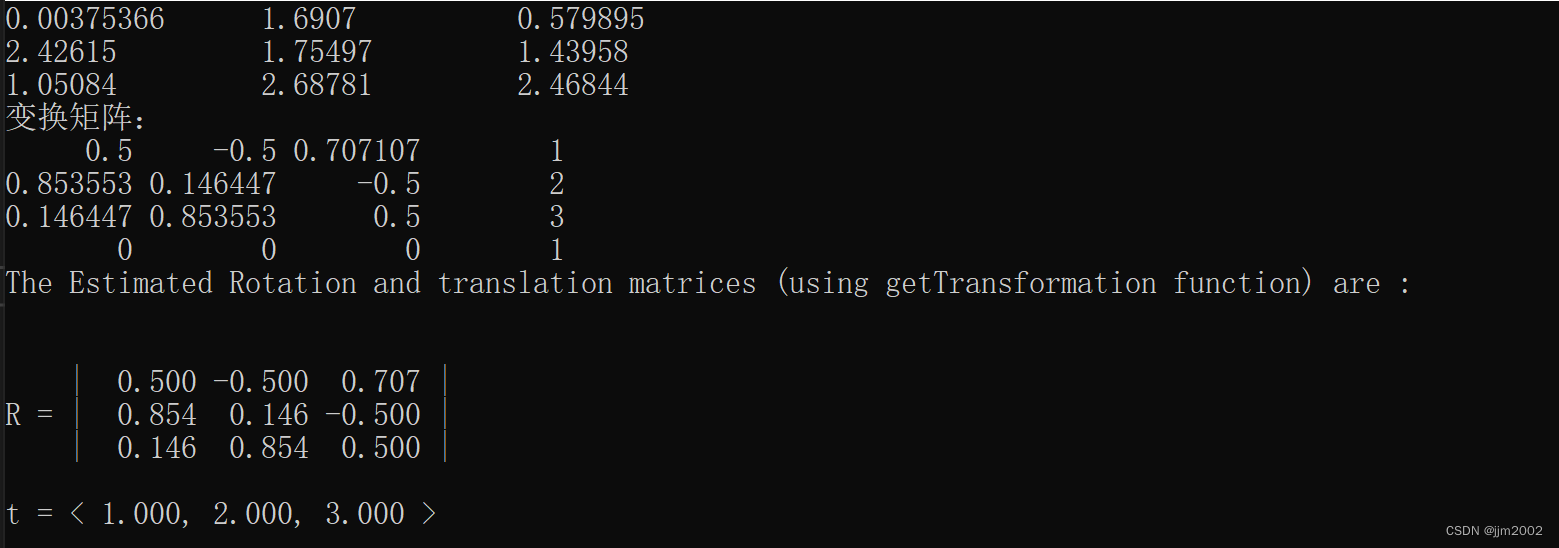
结果：