一、数列基础
1. 判断数列an是否有界
判断|an|是否小于等于M

2. 判断数列an是否单调
对所有正整数n,有an+1>an,则称的单调递增数列。
对所有正整数n,有an+1<an,则称的单调递减数列。
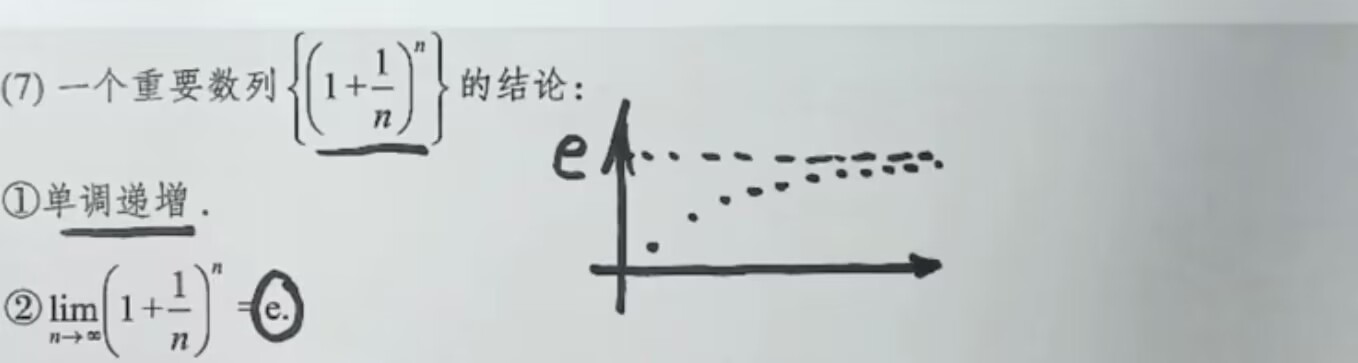
3. 重要数列
二、数列极限的定义

三. 数列收敛
- 若数列{an}收敛,则其任何子列也收敛,且收敛于同一个数。
- 子数列收敛,原数列不一定收敛
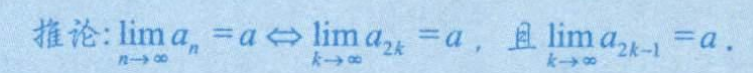
1、 证明收敛性
n趋于∞时,数列an趋于a,则说明该数列收敛。如果有(-1)n,则需要讨论奇偶
2、 判断数列发散

3、重要证明

四、收敛数列的性质

保号性

+99练习


五、四则运算

六、夹逼准则
掌握常见的放缩+重要不等式
具体看书30讲
七、单调有界准则
单调有界数列必有极限,即若数列{xn}单调增加(减少)且有上界(下界),则 lim n → ∞ x \lim \limits_{n \to ∞}x n→∞limxn存在.
八、证明数列单调性常用方法