提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 1.数据库引擎
- 1.1 Ordinary 默认数据库引擎
- 1.2 MySQL 数据库引擎
- MySQL 引擎语法
- 字段类型的映射
- 2.ClickHouse 表引擎
- 3.Log 系列表引擎
- 几种 Log 表引擎的共性是:
- 它们彼此之间的区别是:
- 3.1 TinyLog
- 3.2 StripeLog
- 3.3 Log
- 4.Special 系列表引擎
- 4.1 Memory
- 4.2 Merge
- 4.3 Distributed
1.数据库引擎

- ClickHouse 中支持在创建数据库时指定引擎,目前比较常用的两种引擎为默认引擎
和 MySQL 数据库引擎。
1.1 Ordinary 默认数据库引擎
Ordinary 就是 ClickHouse 中默认引擎,如果不指定数据库引擎创建的就是Ordinary 数据库引擎,在这种数据库下面可以使用任意表引擎。创建时需要注意,Ordinary 首字母需要大写,不然会抛出异常。
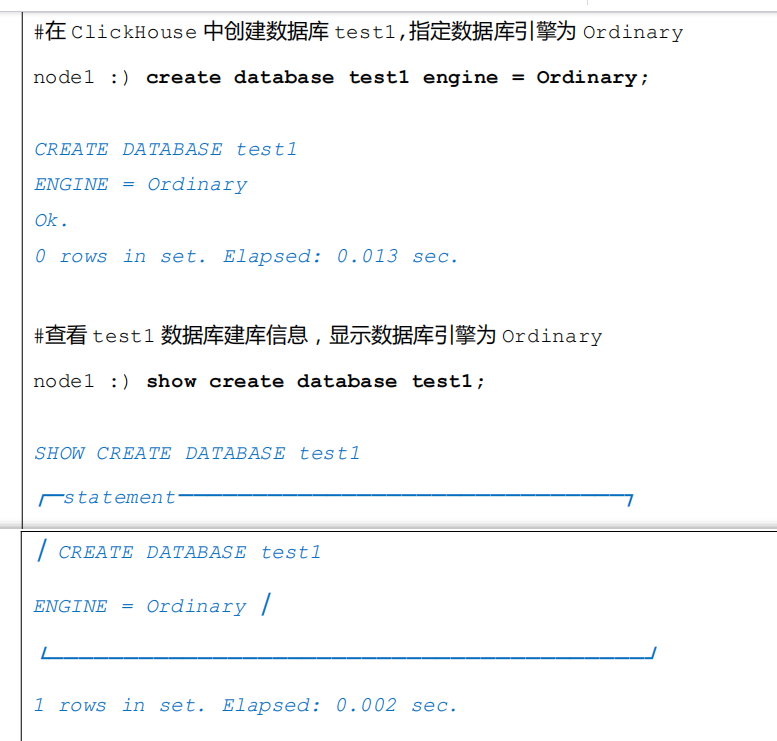

1.2 MySQL 数据库引擎
MySQL 引擎用于将远程的 MySQL 服务器中的表映射到 ClickHouse 中,并允许对表进行INSERT 插入和 SELECT 查询,方便在 ClickHouse 与 MySQL 之间进行数据交换。
- 这里不会将 MySQL 的数据同步到 ClickHouse 中,ClickHouse 就像一个壳子,可以将 MySQL 的表映射成ClickHouse 表,使用 ClickHouse 查询 MySQL 中的数据,在 MySQL 中进行的 CRUD 操作,可以同时映射到 ClickHouse 中。
- MySQL 数据库引擎会将对其的查询转换为 MySQL 语法并发送到 MySQL 服务器中,因此可以执行诸如 SHOW TABLES 或 SHOW CREATE TABLE 之类的操作,但是不允许创建表、修改表、删除数据、重命名操作
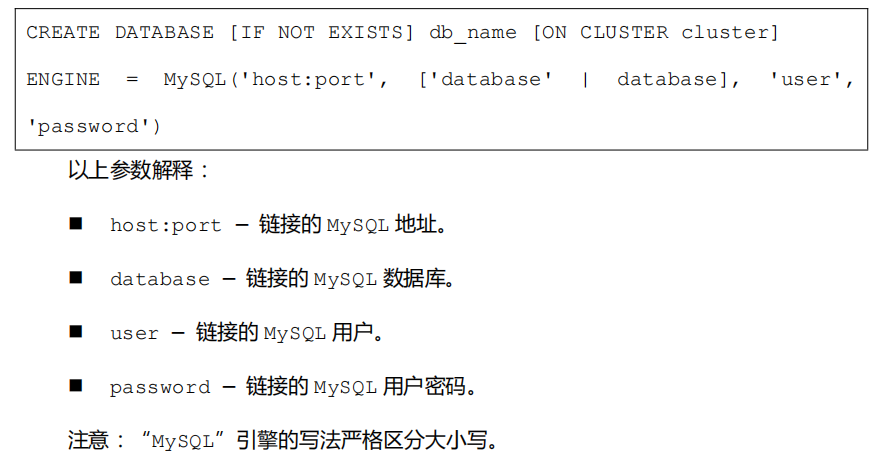
MySQL 引擎语法
ClickHouse 中创建库使用 MySQL 引擎语法如下:
字段类型的映射
- 在 ClickHouse 中使用 MySQL 引擎建库,将 MySQL 库中数据映射到 ClickHouse中,mysql 库中表字段类型与 ClickHouse 表字段类型的映射如下,这里每种类型在ClickHouse 中都支持 Nullable,即可空。
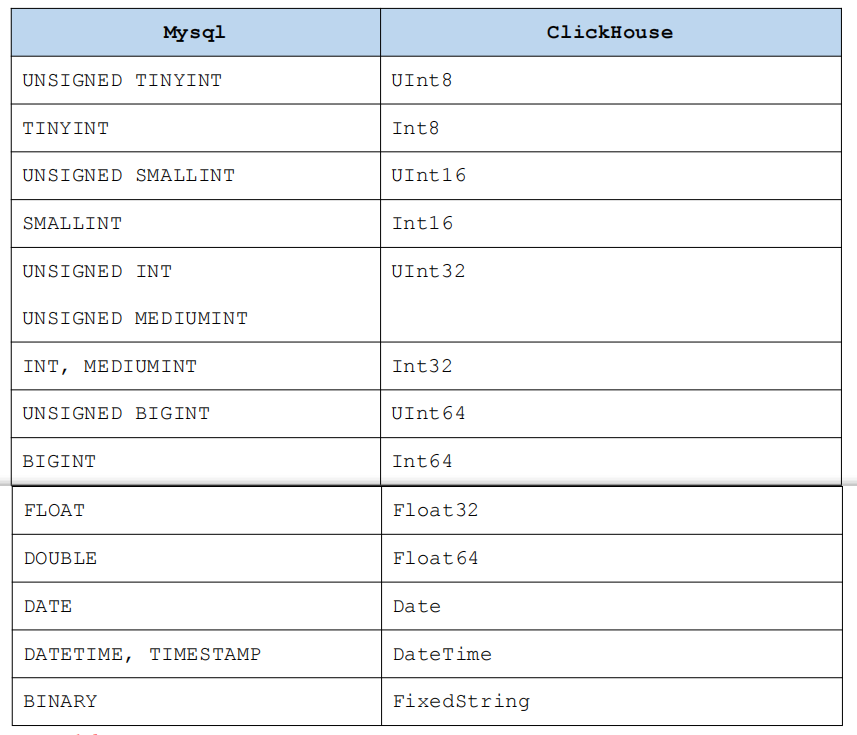

2.ClickHouse 表引擎
MySQL 的数据表有 InnoDB 和 MyISAM 存储引擎,不同的存储引擎提供不同的存储机制、索引方式等功能,也可以称之为表类型。在 ClickHouse 中也有表引擎。
表引擎在 ClickHouse 中的作用十分关键,直接决定了
- 数据如何存储和读取
- 是否支持并发读写
- 是否支持 index 索引
- 支持的 query 种类
- 是否支持主备复制
ClickHouse 提供了大约 28 种表引擎,各有各的用途 纷繁复杂。ClickHouse 表引擎一共分为四个系列,分别是 Log 系列、MergeTree 系列、Integration 系列、Special 系列。其中包含了两种特殊的表引擎 Replicated、Distributed,功能上与其他表引擎正交,根据场景组合使用
- Log 系列用来做小表数据分析
- MergeTree 系列用来做大数据量分析
- Integration 系列则多用于外表数据集成。
- 再考虑复制表 Replicated 系列
- 分布式表 Distributed 等,
3.Log 系列表引擎
Log 系列表引擎功能相对简单,主要用于快速写入小表(1 百万行左右的表),然后全部读出的场景,即一次写入,多次查询。
Log 系列表引擎包含:
- TinyLog、
- StripeLog、
- Log
几种 Log 表引擎的共性是:
-
数据被顺序 append 写到本地磁盘上。
-
不支持 delete、update 修改数据。
-
不支持 index(索引)。
-
不支持原子性写。如果某些操作(异常的服务器关闭)中断了写操作,则可能会获
得带有损坏数据的表。 -
insert 会阻塞 select 操作。当向表中写入数据时,针对这张表的查询会被阻塞,
直至写入动作结束。
它们彼此之间的区别是:
- TinyLog:不支持并发读取数据文件,查询性能较差;格式简单,适合用来暂存
中间数据。 - StripLog:支持并发读取数据文件,查询性能比 TinyLog 好;将所有列存储在
同一个大文件中,减少了文件个数。 - Log:支持并发读取数据文件,查询性能比 TinyLog 好;每个列会单独存储在一
个独立文件中。

3.1 TinyLog
TinyLog 是 Log 系列引擎中功能简单、性能较低的引擎。
- 它的存储结构由数据文件和元数据两部分组成。其中,数据文件是按列独立存储的,也就是说每一个列字段都对应一个文件。
- 由于 TinyLog 数据存储不分块,所以不支持并发数据读取,该引擎适合一次写入,多次读取的场景,对于处理小批量中间表的数据可以使用该引擎,这种引擎会有大量小文件,性能会低。
示例:

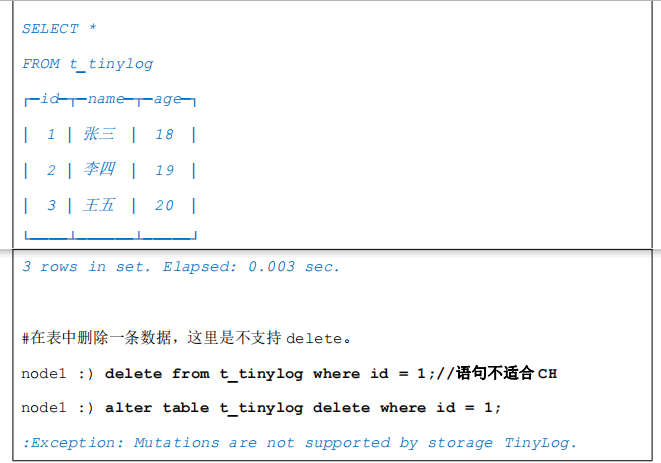
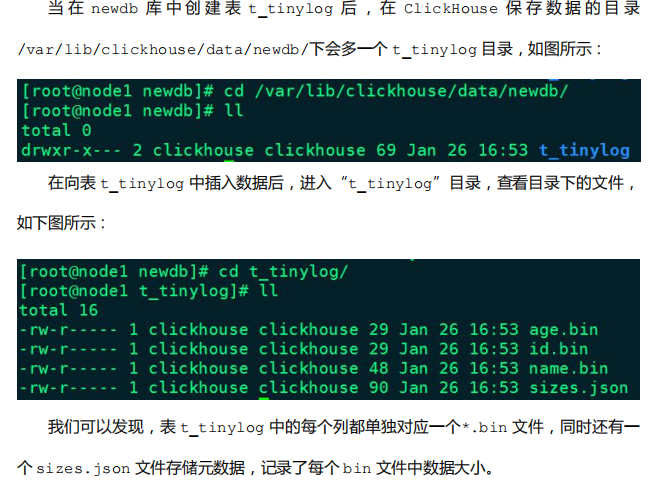
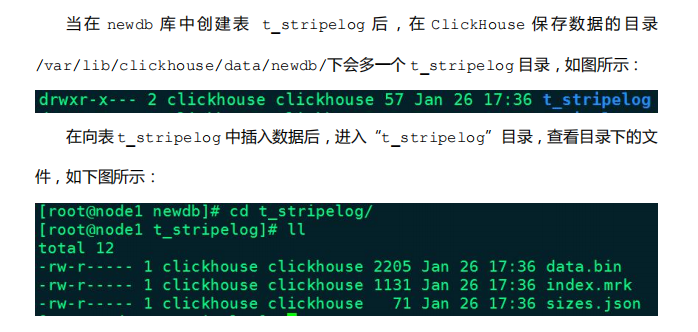
3.2 StripeLog
相比 TinyLog 而言,StripeLog 数据存储会划分块,每次插入对应一个数据块,拥有更高的查询性能(拥有.mrk 标记文件,支持并行查询)
- StripeLog 引擎将所有列存储在一个文件中,使用了更少的文件描述符。对每一次 Insert 请求,ClickHouse 将
数据块追加在表文件的末尾,逐列写入。 - StripeLog 引擎不支持 ALTER UPDATE 和 ALTER DELETE 操作。
示例:


3.3 Log
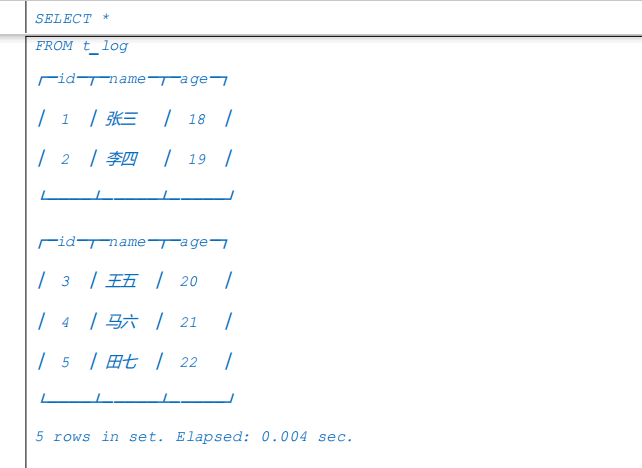
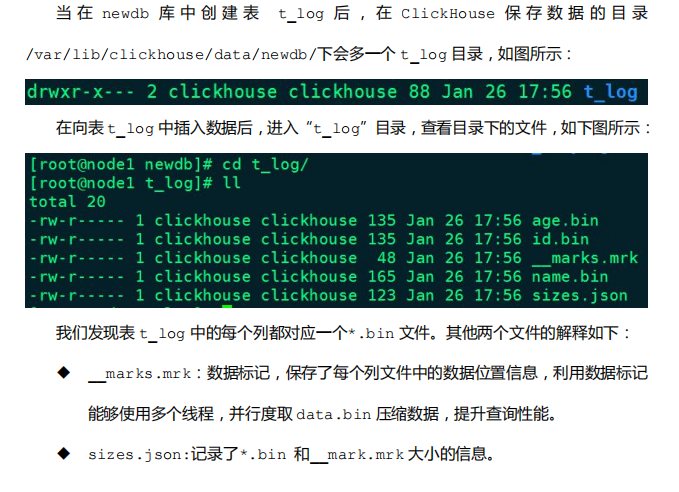
Log 引擎表适用于临时数据,一次性写入、测试场景。Log 引擎结合了 TinyLog 表引擎和 StripeLog 表引擎的长处,是 Log 系列引擎中性能最高的表引擎。
- Log 表引擎会将每一列都存在一个文件中,对于每一次的 INSERT 操作,会生成数据块
- 经测试,数据块个数与当前节点的 core 数一致。
示例:

4.Special 系列表引擎

4.1 Memory
Memory 表引擎直接将数据保存在内存中,ClickHouse 中的 Memory 表引擎具有以下特点:
- Memory 引擎以未压缩的形式将数据存储在 RAM 中,数据完全以读取时获得的形式存储。
- 并发数据访问是同步的,锁范围小,读写操作不会相互阻塞。
- 不支持索引。
- 查询是并行化的,在简单查询上达到最大速率(超过 10 GB /秒),在相对较少的行(最多约 100,000,000)上有高性能的查询。
- 没有磁盘读取,不需要解压缩或反序列化数据,速度更快(在许多情况下,与MergeTree 引擎的性能几乎一样高)。
- 重新启动服务器时,表存在,但是表中数据全部清空。
- Memory 引擎多用于测试。
示例:


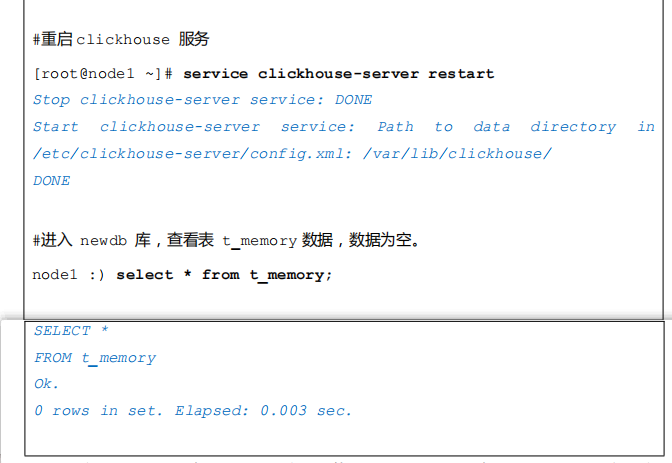
注意:”Memory”表引擎写法固定,不能小写。同时创建好表 t_memory 后,在对应的磁盘目录/var/lib/clickhouse/data/newdb 下没有“t_memory”目录,基于内存存储,当重启 ClickHouse 服务后,表 t_memory 存在,但是表中数据全部清空。
4.2 Merge
Merge 引擎 (不要跟 MergeTree 引擎混淆) 本身不存储数据,但可用于同时从任意多个其他的表中读取数据,这里需要多个表的结构相同,并且创建的 Merge 引擎表的结构也需要和这些表结构相同才能读取。
- 读是自动并行的,不支持写入
- 读取时,那些被真正读取到数据的表如果设置了索引,索引也会被使用。

示例:
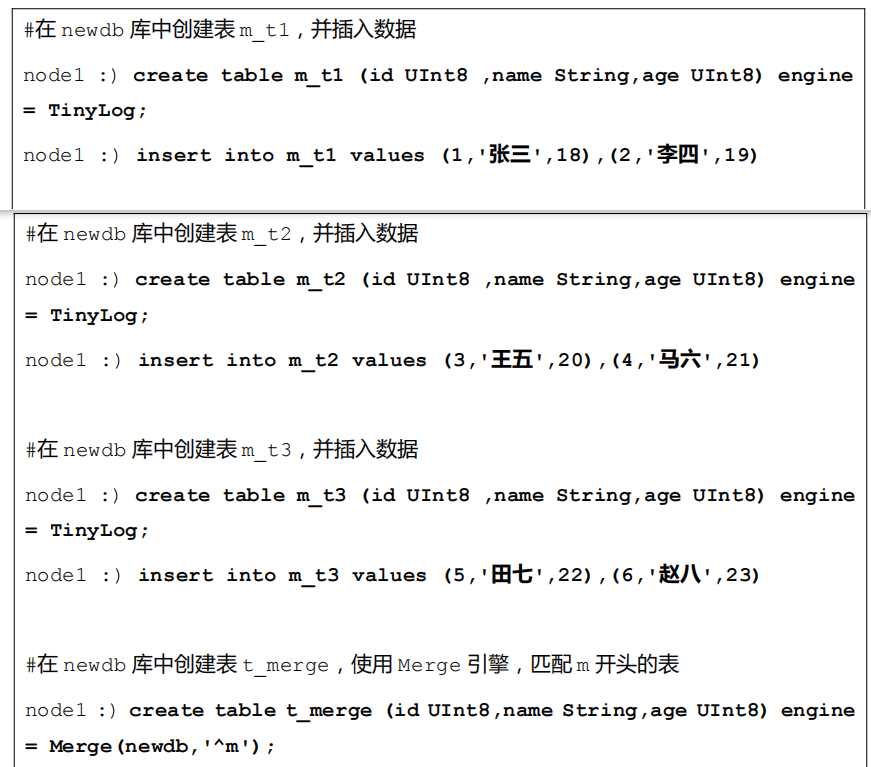

4.3 Distributed
Distributed 是== ClickHouse 中 分 布 式 引 擎== , 之 前 所 有 的 操 作 虽 然 说 是 在ClickHouse 集群中进行的,但是实际上是在 node1 节点中单独操作的,与 node2、node3无关,使用分布式引擎声明的表才可以在其他节点访问与操作。
Distributed 引擎和 Merge 引擎类似,本身不存放数据,功能是在不同的 server上把多张相同结构的物理表合并为一张逻辑表。

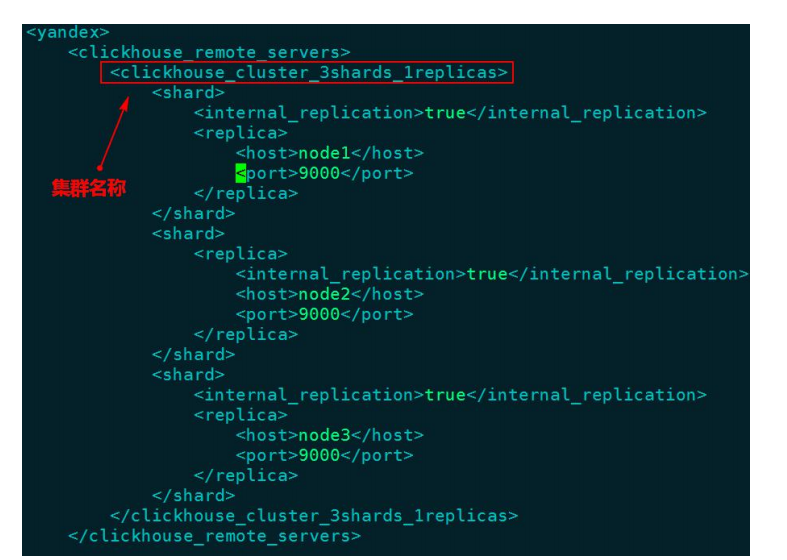

示例:



上面的语句中使用了 ON CLUSTER 分布式 DDL(数据库定义语言),这意味着在集群的每个分片节点上,都会创建一张 Distributed 表,这样便可以从其中任意一端发起对所有分片的读、写请求。