Day 25

01. 组合总和（No. 39）

题目链接

代码随想录题解

1.1 题目

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

1.2 笔记

本题需要求得能使得总和为 target 的结果的集合，和之前的组合的题目非常类似

代码随想录刷题笔记 DAY 25 | 组合问题 No.77 | 组合求和III No.216 | 电话号码的字母组合 No.17

但需要本题的区别是：可以取得相同的元素

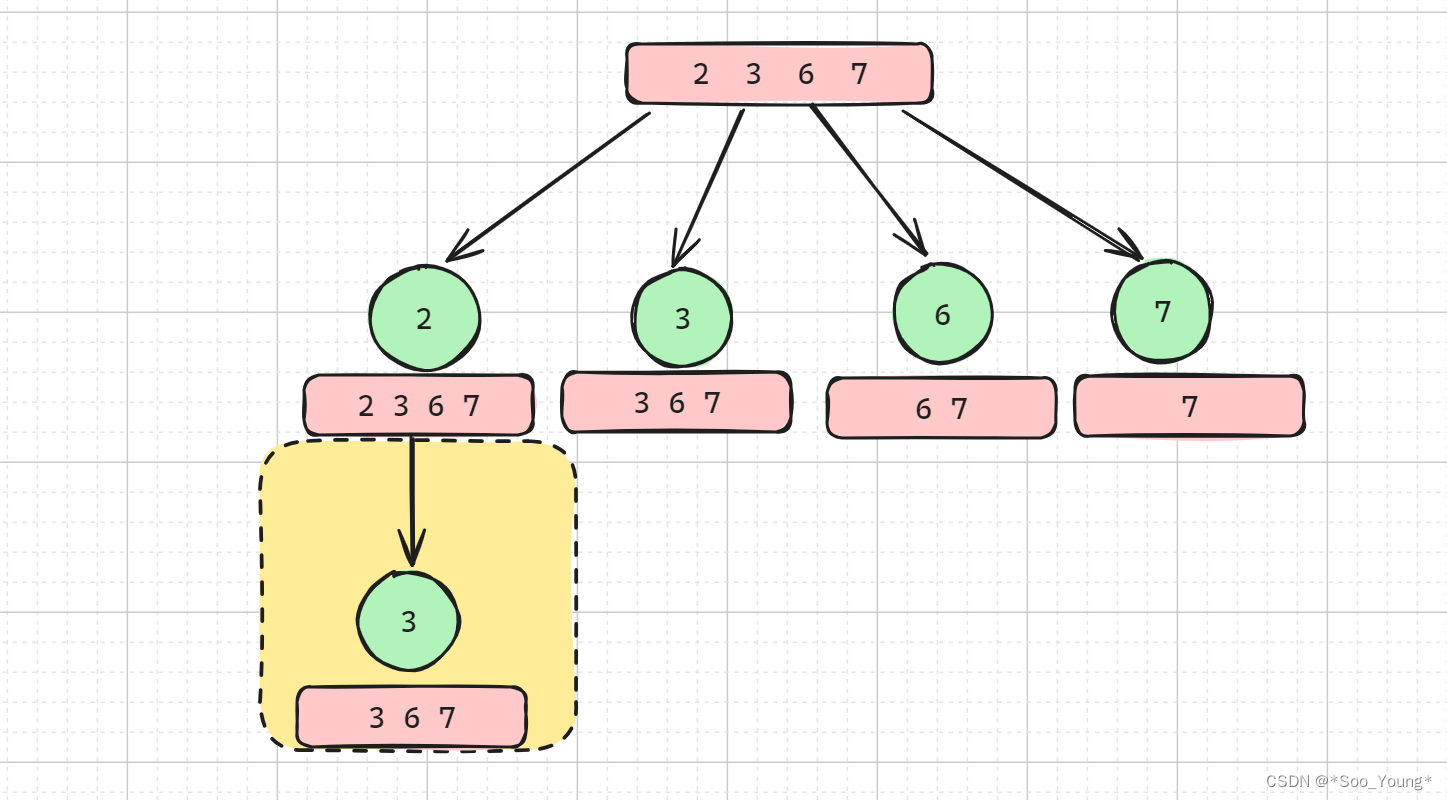
一开始写的时候没有画图，导致写出了这样的代码

for (int i = 0; i < arr.length; i++) {path.add(arr[i]);sum += i;backtracking();path.remove(path.size() - 1);sum -= i;
}

导致结果出现了 2 2 3 和 3 2 2 这样的重复情况。

其实参考上图很容易看出来，对于一个节点的遍历从数组中这节点开始的，所以对于 i 应该限制 startIndex，所以 如果是一个集合求组合 的题目一定要加上 startIndex;

更改代码为：

for (int i = index; i < candidates.length; i++) {path.add(candidates[i]);temp += candidates[i];backtarcking(candidates, target, i);temp -= candidates[i];path.remove(path.size() - 1);
}

写出完整的代码

1.3 代码

class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();int temp = 0;public List<List<Integer>> combinationSum(int[] candidates, int target) {backtracking(candidates, target, 0);return res;}public void backtracking(int[] candidates, int target, int index) {if (temp > target) {index++;return;}if (temp == target) {index++;res.add(new ArrayList(path));}for (int i = index; i < candidates.length; i++) {path.add(candidates[i]);temp += candidates[i];backtracking(candidates, target, i);temp -= candidates[i];path.remove(path.size() - 1);}}
}

02. 组合求和 II（No. 40）

题目链接

代码随想录题解

2.1 题目

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

**注意：**解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

• 1 <= candidates.length <= 100
• 1 <= candidates[i] <= 50
• 1 <= target <= 30

2.2 笔记

这道题目与之前接触到的组合的问题不同的点在于数组中出现了相同的元素，这就会导致这种情况：

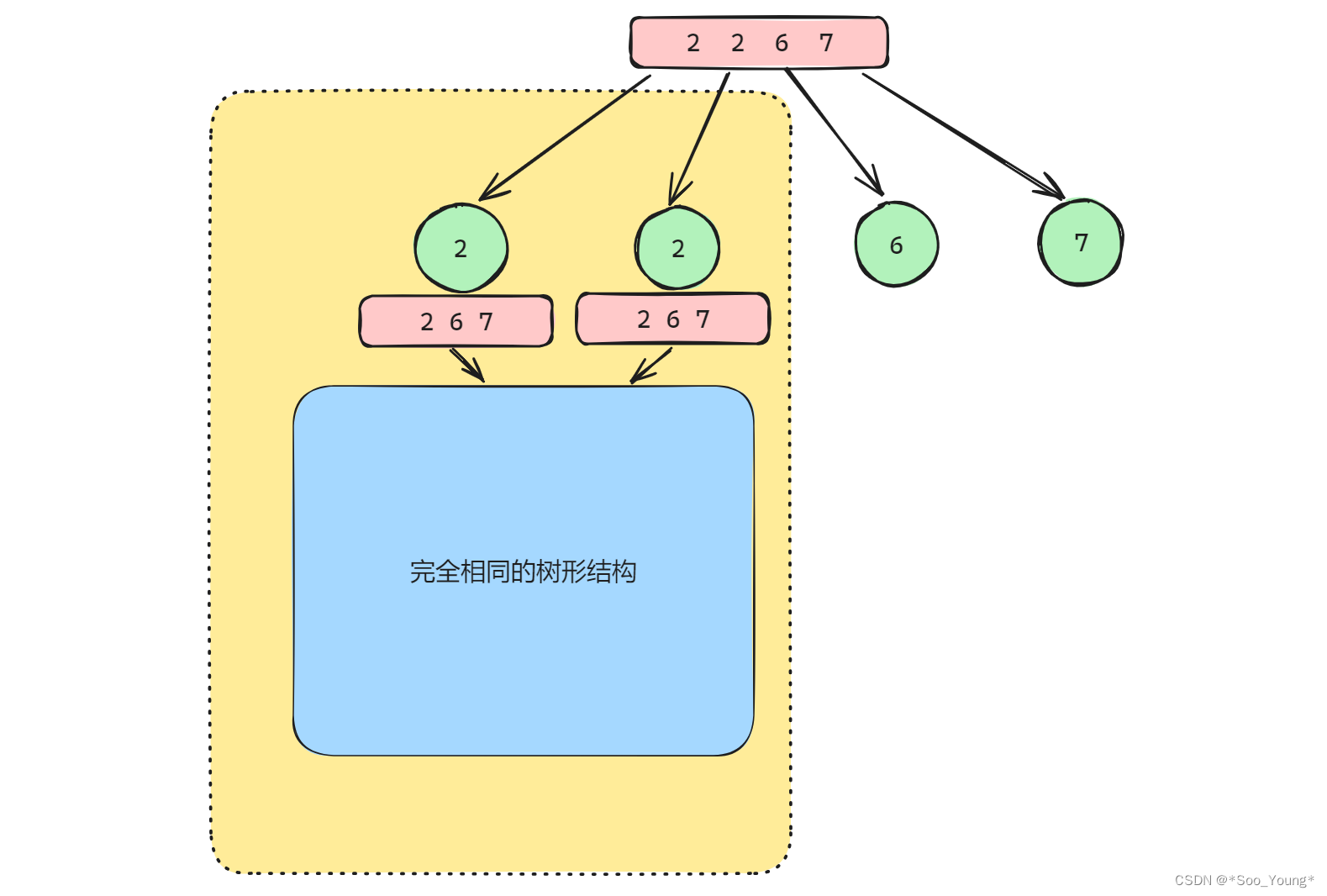
所以要进行去重的操作
❓ 但很容易发现这次的去重好像和之前的不相同？

💡 之前的去重操作是通过控制 i = index，通过每次递归修改 i 的值来使得不会取得相同的元素

也就是对一个 路径 去做去重操作；但本题显然是不只是需要对路径进行去重，还需要对 一层中 遍历到相同的元素的时候进行去重操作。

所以在进行一层中的分枝操作也就是 for 循环遍历的时候，有些节点需要 跳过，比如上图中的两个 2 节点，剩下的内容其实和其他的组合问题没什么区别。

如果要跳过的话首先要对数组进行排序（将相同的数字放到一起），在执行 for 循环的时候，如果遇到和前面相同的就跳过。

for (int i = index; i < candidates.length; i++) {if ( i > index && candidates[i] == candidates[i - 1] ) {continue;}// 其他逻辑
}

2.3 代码

class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();int temp = 0;public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates);backtracking(candidates, target, 0);return res;}public void backtracking(int[] candidates, int target, int index) {if (temp > target) {return;}if (temp == target) {res.add(new ArrayList<>(path));return;}for (int i = index; i < candidates.length; i++) {if ( i > index && candidates[i] == candidates[i - 1] ) {continue;}temp += candidates[i];path.add(candidates[i]);backtracking(candidates, target, i + 1);temp -= candidates[i];path.remove(path.size() - 1);}}
}

03. 分割回文串（No. 131）

题目链接

代码随想录题解

3.1 题目

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = “aab”
输出：[[“a”,“a”,“b”],[“aa”,“b”]]

示例 2：

输入：s = “a”
输出：[[“a”]]

提示：

• 1 <= s.length <= 16
• s 仅由小写英文字母组成

3.2 笔记

分割字符串和组合问题非常类似，先将树形结构画出：

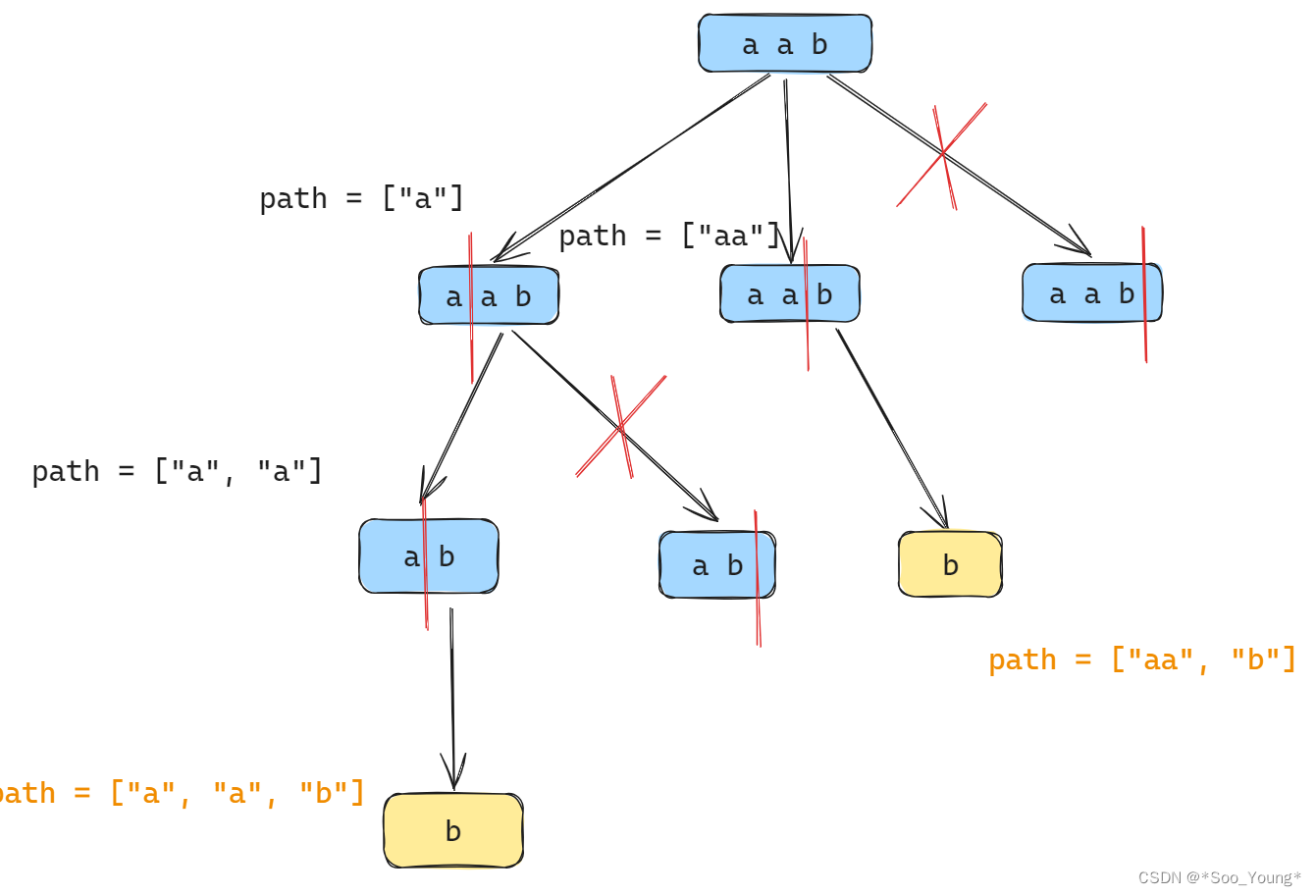
在一层中，遍历的是本层的 字符串 的所有的切割情况，而向下层传递的是 切割后 的字符串的所有的切割情况，其实和组合问题是十分类似的。

单层中切割通过遍历来完成，比如 aab 在第一个 a 的位置切割就是通过将字符串从 start 到 i 来分割

for (int i = startIndex; i < s.length(); i++) {s.substring(startIndex, i + 1); // 单层中切割字符串
}

通过 i 逐步遍历到最后实现了 本层 的 所有切割情况

❓ 那什么时候说明本层的这种切割情况 可能 能够获得最终的结果呢？

答案就是本层的这种切割方式切割的部分是回文串，也就是从 startIndex 到 i 这一部分

所以需要一个方法来判断这种切割是否是回文串

    /**判断是否是回文字符串*/public boolean isValid(String s, int startIndex, int endIndex) {char[] charArray = s.toCharArray();for (int i = startIndex, j = endIndex; i < j; i++, j--) {if (charArray[i] != charArray[j]) {return false;}}return true;}

通过双指针的遍历方式来确定回文串

如果是回文串的话就继续向深层次递归，反之则取遍历本层的其他可能性

if (isValid(s, startIndex, i)) {path.add(s.substring(startIndex, i + 1));
} else {continue;
}
backtracking(i + 1, s);
path.remove(path.size() - 1);

再来确定递归的终点：

如果 startIndex >= s.length() 的话，就说明已经找到一种情况了因为此时已经分割完成了所有的字符串，如果分割途中出现了非回文字符串就会通过 continue 跳过而不可能使得 startIndex == 0。

3.3 代码

class Solution {List<String> path = new ArrayList<>();List<List<String>> res = new ArrayList<>();public List<List<String>> partition(String s) {backtracking(0, s);return res;}public void backtracking(int startIndex, String s) {if (startIndex >= s.length()) {res.add(new ArrayList(path));return;}for (int i = startIndex; i < s.length(); i++) {if (isValid(s, startIndex, i)) {path.add(s.substring(startIndex, i + 1));} else {continue;}backtracking(i + 1, s);path.remove(path.size() - 1);}}/**判断是否是回文字符串*/public boolean isValid(String s, int startIndex, int endIndex) {char[] charArray = s.toCharArray();for (int i = startIndex, j = endIndex; i < j; i++, j--) {if (charArray[i] != charArray[j]) {return false;}}return true;}
}