算法学习——LeetCode力扣贪心篇2

45. 跳跃游戏 II

45. 跳跃游戏 II - 力扣（LeetCode）

描述

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示

• 1 <= nums.length <= 104
• 0 <= nums[i] <= 1000
• 题目保证可以到达 nums[n-1]

代码解析

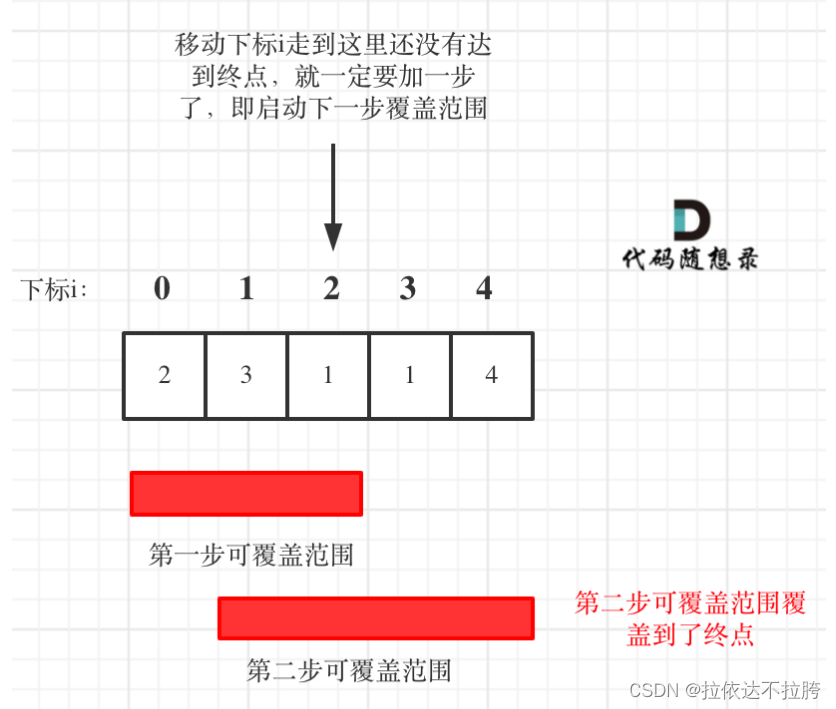
核心思想：当前范围内走不到目的地，更新下一个范围。下一个范围是当前范围内能走到的最远点

class Solution {
public:int jump(vector<int>& nums) {if (nums.size() == 1) return 0;int cover = 0;    // 当前覆盖最远距离下标int step = 0;            // 记录走的最大步数int nextcover = 0;   // 下一步覆盖最远距离下标for (int i = 0; i < nums.size() && i <= cover; i++) {nextcover = max(nums[i] + i, nextcover);  // 更新下一步覆盖最远距离下标if (i == cover) // 遇到当前覆盖最远距离下标{                         if (cover < nums.size() - 1) // 如果当前覆盖最远距离下标不是终点{       step++;       // 需要走下一步cover = nextcover;   // 更新当前覆盖最远距离下标if (nextcover >= nums.size() - 1) break; // 下一步的覆盖范围已经可以达到终点，结束循环} else break;       // 当前覆盖最远距离下标是集合终点，不用做ans++操作了，直接结束}}return step;}
};

1005. K 次取反后最大化的数组和

1005. K 次取反后最大化的数组和 - 力扣（LeetCode）

描述

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

示例

示例 1：

输入：nums = [4,2,3], k = 1
输出：5
解释：选择下标 1 ，nums 变为 [4,-2,3] 。

示例 2：

输入：nums = [3,-1,0,2], k = 3
输出：6
解释：选择下标 (1, 2, 2) ，nums 变为 [3,1,0,2] 。

示例 3：

输入：nums = [2,-3,-1,5,-4], k = 2
输出：13
解释：选择下标 (1, 4) ，nums 变为 [2,3,-1,5,4] 。

提示

• 1 <= nums.length <= 104
• -100 <= nums[i] <= 100
• 1 <= k <= 104

代码解析

对数组可以k次取反，可以对一个元素多次取反
当数组中负数的个数大于k，则从小开始对k个取反
当数组中的负数个数为n小于k，先对负数的n个取反。之后重新排序，计算k-n对2取余
当k-n可以整除2，则意味着对一个负数多次操作后还是正的，不影响结果
当k-n不能整除2，一定会最后有一个负数，则对最小的正数取反。

class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {int sum=0;sort(nums.begin(),nums.end());//判断当前值是负数并且在k个范围内for(int i=0 ; k>0 && nums[i] <=0 && i<nums.size(); i++,k--){nums[i] = -nums[i];} sort(nums.begin(),nums.end());if(k%2 == 1) nums[0] = -nums[0];for(int i =0; i  < nums.size(); i++)  sum += nums[i];return sum;}
};

134. 加油站

134. 加油站 - 力扣（LeetCode）

描述

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

示例

示例 1:

输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

示例 2:

输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。
因此，无论怎样，你都不可能绕环路行驶一周。

提示

• gas.length == n
• cost.length == n
• 1 <= n <= 105
• 0 <= gas[i], cost[i] <= 104

代码解析

先找可能存在开始点，再验证（超时）

先找到所有加油比消耗大的站点，是可能的开始点
然后依次验证上述点，发现油箱是负数的该点无效。发现科研走到开始点前一个并能到下一个的成功

class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int volume = 0;vector<int> start;for(int i=0 ; i<gas.size() ;i++){if(gas[i] >= cost[i]) start.push_back(i); //找到可能开始的点}for(int i=0 ; i < start.size() ;i++){int result = start[i];//    cout<<"result:"<<result<<endl;for(int j = result ; j <= gas.size(); j++) //验证点是否正确{if(j == gas.size()) j = 0; //循环数组volume += gas[j];volume -= cost[j];// cout<<j<<' '<<volume<<endl;if(volume < 0 )  //检查油箱{volume=0;break;}if((result == 0 && j== gas.size()-1 && volume >= 0)||(result!=0 && j == result-1 && volume >= 0 ) ) //验证点成功return result;}}return -1;}
};

贪心算法

可以换一个思路，首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈，说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。

每个加油站的剩余量rest[i]为gas[i] - cost[i]。

i从0开始累加rest[i]，和记为curSum，一旦curSum小于零，说明[0, i]区间都不能作为起始位置，因为这个区间选择任何一个位置作为起点，到i这里都会断油，那么起始位置从i+1算起，再从0计算curSum。

那么为什么一旦[0，i] 区间和为负数，起始位置就可以是i+1呢，i+1后面就不会出现更大的负数？

如果出现更大的负数，就是更新i，那么起始位置又变成新的i+1了。

那有没有可能 [0，i] 区间 选某一个作为起点，累加到 i这里 curSum是不会小于零呢

如果 curSum<0 说明 区间和1 + 区间和2 < 0， 那么 假设从上图中的位置开始计数curSum不会小于0的话，就是 区间和2>0。

区间和1 + 区间和2 < 0 同时 区间和2>0，只能说明区间和1 < 0， 那么就会从假设的箭头初就开始从新选择其实位置了。

那么局部最优：当前累加rest[i]的和curSum一旦小于0，起始位置至少要是i+1，因为从i之前开始一定不行。全局最优：找到可以跑一圈的起始位置。

class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int curSum = 0;int totalSum = 0;int start = 0;for (int i = 0; i < gas.size(); i++) {curSum += gas[i] - cost[i]; //当前油箱totalSum += gas[i] - cost[i];//全局油箱if (curSum < 0) {   // 当前累加rest[i]和 curSum一旦小于0start = i + 1;  // 起始位置更新为i+1curSum = 0;     // curSum从0开始}}if (totalSum < 0) return -1; // 说明怎么走都不可能跑一圈了return start;}
};

135. 分发糖果

135. 分发糖果 - 力扣（LeetCode）

描述

n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

你需要按照以下要求，给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

示例

示例 1：

输入：ratings = [1,0,2]
输出：5
解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例 2：

输入：ratings = [1,2,2]
输出：4
解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

提示

• n == ratings.length
• 1 <= n <= 2 * 104
• 0 <= ratings[i] <= 2 * 104

代码解析

class Solution {
public:int candy(vector<int>& ratings) {int sum=0 ;vector<int> num(ratings.size(),1);for(int i=0 ; i < ratings.size()-1 ;i++ ) //正向，发现分高的孩子多给一个糖{if(ratings[i+1] > ratings[i]) num[i+1] = num[i]+1;}for(int i= ratings.size()-1 ; i >=1 ;i-- )//反向，发现分高的孩子多给一个糖{if(ratings[i] < ratings[i-1]) num[i-1] = max(num[i]+1 , num[i-1]) ;// 找最大的}for(auto it:num)  sum += it;return sum;}
};

860. 柠檬水找零

860. 柠檬水找零 - 力扣（LeetCode）

描述

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例

示例 1：

输入：bills = [5,5,5,10,20]
输出：true
解释：
前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零，所以我们输出 true。

示例 2：

输入：bills = [5,5,10,10,20]
输出：false
解释：
前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
由于不是每位顾客都得到了正确的找零，所以答案是 false。

提示

• 1 <= bills.length <= 105
• bills[i] 不是 5 就是 10 或是 20

代码解析

class Solution {
public:bool lemonadeChange(vector<int>& bills) {int volume = 0 , diff = 0;int num_5 ,num_10 ;map<int,int> my_map;my_map[5]=0;my_map[10]=0;for(int i=0 ; i < bills.size() ;i++){ if(bills[i]==5) my_map[5]++;else if( bills[i]==10 ) {my_map[10]++;my_map[5]--;}else if(bills[i]==20){if(my_map[10] > 0) //给20的优先找10块的{my_map[10]--;my_map[5]--;}else{my_map[5] = my_map[5] -3;}}if(my_map[5] < 0 || my_map[10] < 0) return false;}return true;}
};