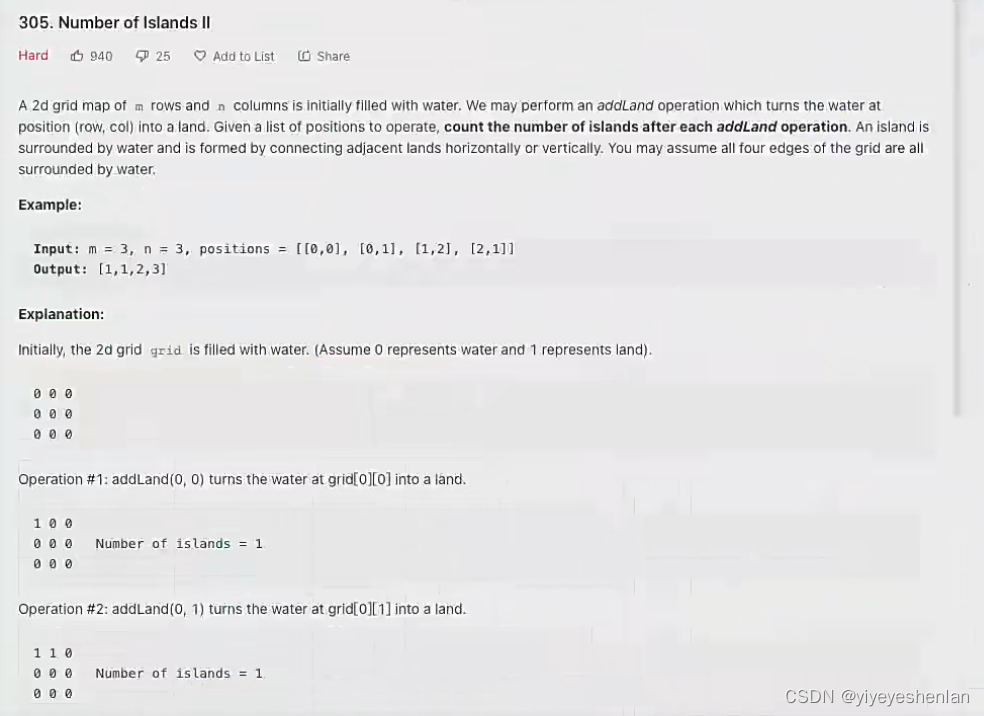
A. Recovering a Small String(枚举)

思路
每次枚举每一位
#include <iostream>
using namespace std;int main() {int t;cin >> t;for (int i = 0; i < t; i++) {int n;cin >> n;if(n <= 28){cout<<"aa"<<char(n - 3 + 'a')<<endl;}else if(n <= 53){cout<<'a'<<char(n - 1 - 27 + 'a')<<'z'<<endl;}else{cout<<char(n - 1 - 52 + 'a')<<"zz"<<endl;}}return 0;
}
B. Make Equal(模拟)

思路
每个容器先减去平均值,然后从前到后累加,如果值小于0了,那么就说明不可能
#include<iostream>
using namespace std;
int t, n;
int a[200005];int main(){scanf("%d", &t);while(t--){scanf("%d", &n);int sum = 0;for(int i = 1; i <= n; i++){scanf("%d", &a[i]);sum += a[i];}sum /= n;for(int i = 1; i <= n; i++){a[i] -= sum;}int res = 0, f = 1;for(int i = 1; i <= n; i++){if(a[i] >= 0) res += a[i];else{res += a[i];if(res < 0){f = 0;break;}}}if(f) printf("YES\n");else printf("NO\n");}return 0;
}
C. Make Equal Again(贪心)

思路
因为不超过1次,那么判断如果左端不等于右端,那就取最大值那端,否则都取
#include <iostream>
using namespace std;
const int N = 2e5 + 10;
int a[N], n, t;int main() {cin >> t;while (t--) {cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];}int l = 1;for(int i = 2; i <= n; i++){if(a[i] == a[l]) l++;else break;}int r = n;for(int i = n - 1; i > 0; i--){if(a[i] == a[r]) r--;else break;}if(l >= r){cout<<0<<endl;continue;}r = n - r + 1;long long ans;if(a[1] == a[n]) ans = n - l - r;else ans = n - max(l, r);cout<<ans<<endl;}return 0;
}
D. Divisible Pairs(同余)

思路
(ai + aj) % x 同余 0, (ai - aj) % y 同余 0,简写成 ai + aj ≡ 0(mod x)
移项得:aj ≡ -ai(mod x), aj ≡ ai(mod y)
即:ai % x, ai % y 找 -ai % x, ai % y
#include<iostream>
#include<map>
using namespace std;
const int N = 2e5 + 10;
int n, a[N];int main(){int t, x, y;scanf("%d", &t);while(t--){// 统计每对元组的数量 map<pair<int, int>, int> mp;scanf("%d%d%d", &n, &x, &y);for(int i = 0; i < n; i++){scanf("%d", &a[i]);mp[make_pair(a[i] % x, a[i] % y)]++;}long long ans = 0;for(int i = 0; i < n; i++){mp[make_pair(a[i] % x, a[i] % y)]--;// (x - a[i] % x)转化成一个正数,再 % x,防止出现负数 ans += mp[make_pair((x - a[i] % x) % x, a[i] % y)];}printf("%lld\n", ans);}return 0;
}
E. Anna and the Valentine’s Day Gift(贪心)

思路
整数大于等于 10 ^ m -> 整数是 m + 1 位,男合并,女翻转
女想赢,那么会把 111000 翻转成 000111
男想赢,那么会合并 1100 111 成 1100111
按末尾 0 的长度降序排序,该谁操作,就谁取最优
用优先队列存储,大根堆
#include<iostream>
#include<queue>
using namespace std;
const int N = 2e5 + 10;
int n;int main(){int t, m, x;scanf("%d", &t);while(t--){// 统计后缀 0 的个数和当前数的位数,大根堆 priority_queue<pair<int, int>> q;scanf("%d%d", &n, &m);for(int i = 0; i < n; i++){int z = 0, w = 0, cnt = 0, len = 0;scanf("%d", &x);z = x;while(z % 10 == 0){cnt++;z /= 10;}w = x;while(w){len++;w /= 10;}q.push(make_pair(cnt, len));}//判断是谁的回合,0 是 Anna,1 是 Sasha int f = 0, sa = 0;while(q.size()){auto it = q.top();// Sasha 操作,合并 if(f) sa += it.second;// Anna 操作,消除 0 else sa += it.second - it.first;f ^= 1;q.pop();}if(sa >= m + 1) printf("Sasha\n");else printf("Anna\n");}return 0;
}
F. Chat Screenshots(拓扑排序)

思路
如果每个点的入度都为 0 了,那就说明序列正确了,否则是有环
记得判重,每次数组初始化为 memset(h, -1, sizeof(int) * (n * k + 1));
#include<iostream>
#include<cstring>
using namespace std;
const int N = 2e5 + 10;
int h[N], e[N], ne[N], idx;
int q[N], hh, tt = -1;
int n, k, x, y;
int d[N], st[N];
int t;void solve(){scanf("%d%d", &n, &k);int zz = n * k + 1;memset(h, -1, sizeof(int) * zz);memset(e, 0, sizeof(int) * zz);memset(ne, 0, sizeof(int) * zz);idx = 0;memset(q, 0, sizeof(int) * zz);hh = 0, tt = -1;memset(d, 0, sizeof(int) * zz);memset(st, 0, sizeof(int) * zz);for(int i = 1; i <= k; i++){scanf("%d", &x);for(int j = 2; j <= n; j++){scanf("%d", &y);if(j != 2){//判重int f = 1;for(int ii = h[x]; ii != -1; ii = ne[ii]){int j = e[ii];if(j == y){f = 0;}}//添加一条 x -> y 的边if(f){e[idx] = y;ne[idx] = h[x];h[x] = idx++;d[y]++; }}x = y;}}//for(int i = 1; i <= n; i++) cout<<d[i]<<endl;for(int i = 1; i <= n; i++){if(!d[i]){q[++tt] = i;st[i] = 1;} }//cout<<"----------"<<endl;while(hh <= tt){int it = q[hh++];//cout<<it<<" ";for(int i = h[it]; i != -1; i = ne[i]){int j = e[i];if(!st[j]){d[j]--;if(!d[j]) q[++tt] = j;}}}for(int i = 1; i <= n; i++){//cout<<d[i]<<endl;if(d[i] > 0){printf("NO\n");return;}}printf("YES\n");
}int main(){scanf("%d", &t);while(t--){solve();}return 0;
}
G. One-Dimensional Puzzle(排列组合)
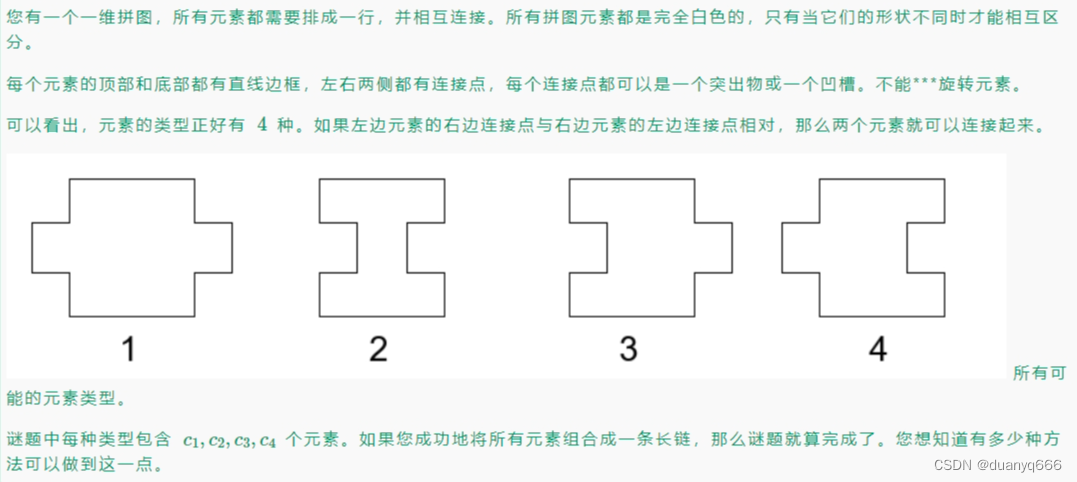
思路
在 1、2 之间插入 3、4 有多少种方法


#include<iostream>
using namespace std;
const int p = 998244353;int qm(int a, int b){int res = 1 % p;while(b){if(b & 1) res = (long long)res * a % p;a = (long long)a * a % p;b >>= 1;}return res;
}int C(int a, int b){int res = 1;for(int i = 1, j = a; i <= b; i++, j--){res = (long long)res * j % p;res = (long long)res * qm(i, p - 2) % p;}return res;
}int lucas(long long a, long long b){if(a < p && b < p) return C(a, b);return (long long)C(a % p, b % p) * lucas(a / p, b / p) % p;
}signed main(){int n;long long a, b, c, d;cin>>n;while(n--){cin>>a>>b>>c>>d;long long ans = 0; // 初始化 ansif(a == 0 && b == 0){if(c > 0 && d > 0){printf("0\n");}else{printf("1\n");}}else if(a - b == 1){ans = (long long)lucas(a + c - 1, c) * lucas(a + d - 1, d) % p; // 添加取模操作printf("%lld\n", ans);}else if(b - a == 1){ans = (long long)lucas(b + c - 1, c) * lucas(b + d - 1, d) % p; // 添加取模操作printf("%lld\n", ans);}else if(a == b){ans = ((long long)lucas(a + c - 1, c) * lucas(a + d, d) % p + (long long)lucas(a + c, c) * lucas(a + d - 1, d) % p) % p; // 添加取模操作printf("%lld\n", ans);}else{printf("0\n");}}return 0;
}