数据检索：倒排索引加速、top-k和k最邻近-编程知识

之前在https://www.yuque.com/treblez/qksu6c/wbaggl2t24wxwqb8?singleDoc# 《Elasticsearch: 非结构化的数据搜索》我们看了ES的设计，主要侧重于它分布式的设计以及LSM-Tree，今天我们来关注算法部分：如何进行检索算法的设计以及如何加速倒排索引。然后看看topk的面试热门题如何解决。

状态检索：bitmap的哈希函数公式

bitmap的最优hash函数的计算公式为：
k = (m/n)*ln2
其中m为bit数组的长度，n为要存入的对象个数。

加速倒排索引和Roaring Map

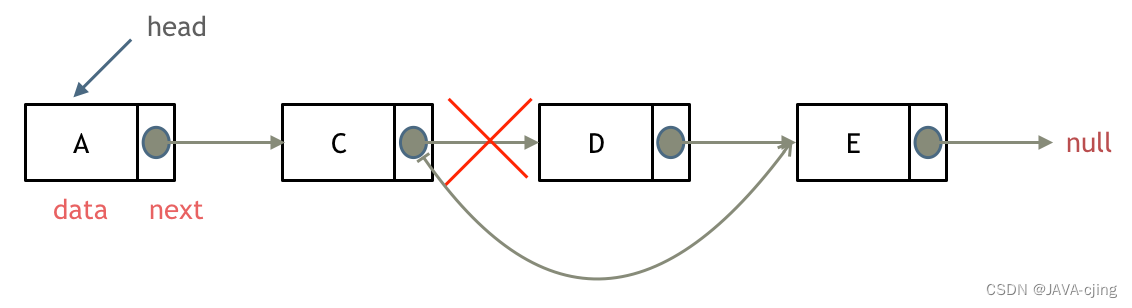
倒排索引由key和posting list构成，posting list可以用很多结构实现，比如红黑树、跳表、链表等。
posting list往往会用于归并过程（join），这里我们很容易想到spark的join策略：嵌套循环、排序归并和哈希归并。他们的复杂度分别是m*n,m+n和n(较大)。
因为posting list天生有序，所以这里主要的策略在于加速排序归并和哈希归并过程。
排序归并可以用跳表和红黑树，双指针相互二分查找将每次搜索的复杂度降低到logk。
Lucene和Elasticsearch就采用了这种方法。
同样，posting list也可以使用哈希表和位图来实现。
普通的哈希表和位图很简单，不再赘述。更广泛使用的是Roaring Bitmap（压缩位图）。
Roaring Bitmap简单来说，就是用高16位哈希到桶的编号，低16位再哈希到bitmap，这样如果元素稀疏的话，就能节省没有bitmap的桶的空间。
低16位桶的数量如果少于4096，那么bitmap就使用数组容器来节省空间，否则使用位图容器。

倒排索引的更新

倒排索引的更新主要有如下方案：

Double Buffer双缓冲 + 原子swap
全量索引+增量索引

增量索引的合并方案：

全量合并
再合并（归并合并）
滚动合并（加入索引级别）

精准打分和非精准打分

精准打分就是采用堆排序算法进行排序。
复杂度是n+klogn。
非精准打分一般用在召回阶段，也就是排序的第一步，一般采用的打分算法有tf-idf和bm25两种。
那么非精准的打分如何实现呢？

静态质量得分截断（比如使用pagerank）
词频得分打分截断（使用胜者表解决相同文档得分不同的情况，选出多于k个结果）
使用分层索引，建立精准索引和非精准索引，不足k个精准结果去非精准索引中补齐

日志的分布式拆分

索引的拆分方式：

基于文档进行拆分
基于前缀进行拆分

※最近的k个人和k最邻近

KNN - 检索最近的k个设施（低维空间的k最近邻）- 四/八叉树、前缀树和k-d树

这两个问题都可以用Geohash编码，但是k最邻近设施比k个人更加复杂。
最近的k个人只需要查找编码的附近8个区域，就可以转换到非精确打分 – > 精确打分的流程中，但是k最邻近则需要不断扩大搜索范围，每次扩大一个搜索层级进行搜索。
为了利用到之前搜索的结果，k最邻近可以使用四叉树（二维），前缀树、八叉树（三维）和k-d树。
检索最近的k个加油站、检索相似文章都是这类问题，相似文章在存储中表示为n维向量中的一个点，也会变成k最邻近设施的问题。

ANN - 过滤相似文档（高维空间的k最近邻）- 局部敏感哈希

当向量的维度太高的时候，k-d树的复杂度会变得很高。这时候，我们会采用局部敏感哈希的方案来处理：
对于高维空间，局部敏感哈希会随机生成n个超平面，每个平面都会将高维空间划分成两个部分，分别编码为0和1，如果有两个点的哈希值的海明距离比较小，那么我们就认为它们邻近。
局部敏感哈希的问题在于它无法保存每个维度的权重信息，Google提出了SimHash来解决这个问题。

ANN - 有权重的高维空间k最近邻-SimHash

simHash会将哈希函数编码中的0和1转换为-1和1，并且乘上权重值，最后将所有关键词的哈希值相加。最后将大于0的值变为1，小于等于0的值变为0.
那么如何在这个基础上进行相似检索呢？
简单的方法是将每一个比特位都当作索引，在召回时分别考虑自己的每一个比特位，进行召回，但是这样产生的数据量很大，google提出的解决方案是抽屉原理：将哈希值平均切为4段，如果两个哈希值的比特位差异不超过3个（海明距离小于等于3），那么至少有一个段的比特位完全相同。
因此，我们可以将每一个文档都根据比特位分为4段，建立4个倒排索引，然后进行召回。

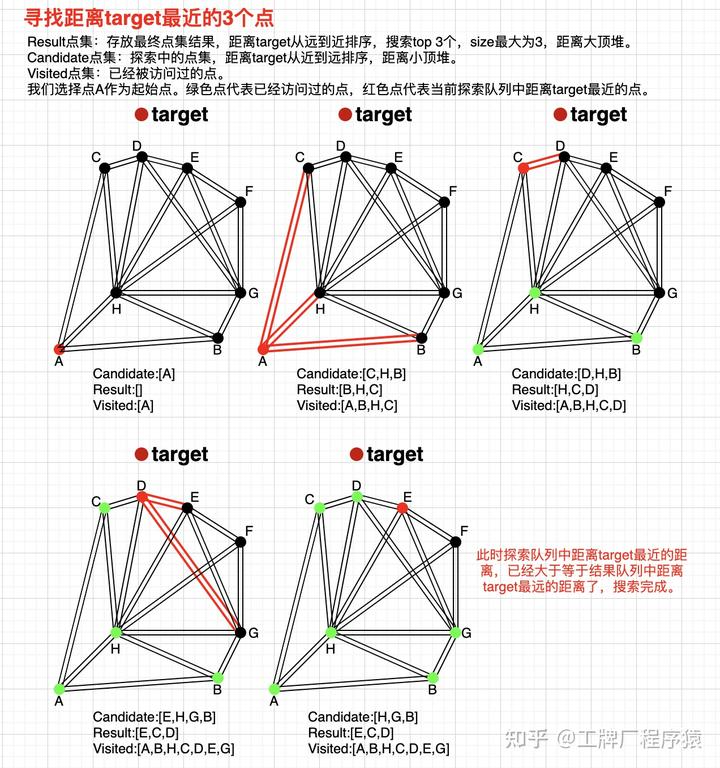
ANN - HNSW

Delaunay图可以保证图中所有的点都有点与之相连，且能保证整张图的边的数量尽可能的少。但实际上，NSW并不是直接采用Delaunay图。Delaunay图有个缺点，它没有高速公路机制，也就是说所有的图节点都只会跟自己相近的点建立连接，如果需要抵达一个距离较远的点，则时间复杂度较高。而不管是构建图索引的时候，还是在线检索的时候，都需要进行临近搜索，直接采用Delaunay图就会导致离线索引构建以及在线serving的时间复杂度不理想。
NSW的图结构是近似的Delaunay图，与Delaunay图不同的是，他有高速公路机制。如图所示。

拍照识花–乘积量化

上面的ANN和KNN算法的问题在于，它们只能用在表面特征的相似性上，而不是本质的相似性上。
在需要本质相似性的领域，比如图像处理上，需要KMeans来进行聚类。
K-means可以将k个聚类id作为倒排索引的key来建立倒排索引。
当要查询一个点邻近的点时，计算该点和所有聚类中心的距离，就可以进行topK的查询。
为了优化存储空间，可以用乘积量化技术进行压缩。

LevelDB的lsm-tree

LevelDB将内存数据分为memtable和immutable table两部分。这两部分数据都使用跳表存储。
当memtable的数据达到存储上限时，将会被转换为immutable table，并且生成一个新的memtable，新的memtable被用来支持新数据的写入和读取。immutable只读，不需要加锁就能写入磁盘。
LevelDB使用LCS（https://www.yuque.com/treblez/qksu6c/wbaggl2t24wxwqb8#seDXd）进行合并，从第一层开始使用归并排序后的结果。
SSTable分为数据存储区（data block）和数据索引区（index block）。
数据索引区从上到下又分为：

过滤器数据区
过滤器索引区
数据索引区对数据存储区的block进行索引格式 key - offset - size
foot block 记录index block和meta index block的大小

SSTable的检索过程和列式存储很像，这里的过滤器都是bloom filter。
使用缓存加速检索SSTable文件的过程
如果在二分查找时，将data block和index block分两次io读入内存，那么开销显然非常大，为了减少这里的开销，LevelDB设计了table cache和block cache两个索引。
table cache存储最近使用的SSTable的index block，block cache存储最近使用的data block。这两个缓存都使用LRU策略替换。
levelDB的一个问题在于如果immutable table还没有写入磁盘，memtable满了，会导致阻塞，google的rocksDB允许创建多个memtable解决了这个问题。
B+树适用于随机读很多，但是写入很少的场景；lsm树进行了大量写操作优化，效率会更高。
在LSM-Tree的L0写入时，限制文件数量，L1及以上则要限制容量大小；写入时会根据beg和end限制本层的一个sstable文件在下一层对应的sstable文件数小于十个，如果达到了十个就会结束文件的生成。