实验十三:数据拟合与数据差值
练习二
1.在飞机的机翼加工时,由于机翼的尺寸很大,所以通常在图纸上只能标出部分关键点的尺寸某型号飞机的机翼上缘轮廓线的部分数据如下:
| x | 0 | 4.74 | 9.05 | 19 | 38 | 76 | 95 | 114 | 133 | 152 | 171 | 190 |
| y | 0 | 5.23 | 8.1 | 11.97 | 16.15 | 16.34 | 14.63 | 12.16 | 6.69 | 7.03 | 3.99 | 0 |
试用线性插值法、三次样条插值法分别绘制机翼上缘轮线的图形
clc;clear;
x=[0,4.74,9.05,19,38,76,95,114,133,152,171,190];
y=[0,5.23,8.1,11.97,16.15,16.34,14.63,12.16,6.69,7.03,3.99,0];
xb=0:190;
yb=interp1(x,y,xb,'linear');%线性插值
ybb=interp1(x,y,xb,'spline');%三次样条插值
figure(1)
plot(xb,yb);
hold on
plot(x,y,'.');
figure(2)
plot(xb,ybb);
hold on
plot(x,y,'.');

2.对函数![]() 在 在区间[-10,10]上做等距拉格朗日插值和分段线性插值,观察插值中出现的龙格现象.要求:
在 在区间[-10,10]上做等距拉格朗日插值和分段线性插值,观察插值中出现的龙格现象.要求:
(1)在区间[-10,10]上取不同的插值结点数n,做出函数![]() 的拉格朗日插值多项式和分段插值多项式;
的拉格朗日插值多项式和分段插值多项式;
format long
clc;clear;
n=50;%在这里可以更改n值
x0=linspace(-10,10,n);
y0=1./(1+25*x0.^2);
x=-10:0.01:10;
y=lglrcz(x0,y0,x);
figure(1)
plot(x0,y0,'.',x,y);
x00=reshape(x0,5,n/5);
y00=reshape(y0,5,n/5);
figure(2)
plot(x0,y0,'.');
yy=[];xxx=[];
for i=1:n/5xx=x00(1,i):0.01:x00(5,i);m=lglrcz(x00(:,i),y00(:,i),xx);xxx=[xxx,xx];yy=[yy,m];
end
hold on
plot(xxx,yy);
function y=lglrcz(x0,y0,x)
n=length(x0);
m=length(x);
for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;
end
end


(2)将曲线![]() 和拉格朗日插值多项式曲线以及分段插值多项式曲线绘在同一坐标系上进行比,随着结点数n的不断增大,通过观察,你发现了什么?
和拉格朗日插值多项式曲线以及分段插值多项式曲线绘在同一坐标系上进行比,随着结点数n的不断增大,通过观察,你发现了什么?
为了对比明显我们取n=10,将两者插值曲线画在一个坐标系上进行对比。
format long
clc;clear;
n=10;%在这里可以更改n值
x0=linspace(-10,10,n);
y0=1./(1+25*x0.^2);
x=-10:0.01:10;
y=lglrcz(x0,y0,x);
x00=reshape(x0,5,n/5);
y00=reshape(y0,5,n/5);
yy=[];xxx=[];
for i=1:n/5xx=x00(1,i):0.01:x00(5,i);m=lglrcz(x00(:,i),y00(:,i),xx);xxx=[xxx,xx];yy=[yy,m];
end
figure(1)
plot(x0,y0,'.',x,y,xxx,yy);
function y=lglrcz(x0,y0,x)
n=length(x0);
m=length(x);
for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;
end
end

通过观察我们发现,采用分段线性插值可以大大削弱龙格现象;当n值较大时,龙格现象十分明显。
3.将区间[-5,5]作n等分,对函数![]() 做拉格朗日插值,观察龙格现象,问:能否取到n使得
做拉格朗日插值,观察龙格现象,问:能否取到n使得![]() ?
?
我们首先假设可以取到n使得上式成立,然后编写以下程序:
format long
clc;clear;
x1=-5:0.001:5;
syms x
f=x/(1+x^4);
for n=50:100x0=linspace(-5,5,n);f0=1;for i=1:nf0=(x-x0(i))*f0;endf1=abs(diff(f,n))*abs(f0)/factorial(n);f1=matlabFunction(f1);h=f1(x1);if max(h)<10^-6return;end
end
n
ff=matlabFunction(f);
plot(x0,ff(x0),'.');
y=lglrcz(x0,ff(x0),x1);
hold on
plot(x1,y);
function y=lglrcz(x0,y0,x)
n=length(x0);
m=length(x);
for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;
end
end
经过程序运行,发现一直无法出来结果。我们推测,可能无法达到题目要求,一直再往后循环,导致数太大一时半会出不来。
不妨我们n取100看一下图像:
format long
clc;clear;
x1=-5:0.01:5;
syms x
f=x/(1+x^4);
n=100;
x0=linspace(-5,5,n);
ff=matlabFunction(f);
plot(x0,ff(x0),'.');
y=lglrcz(x0,ff(x0),x1);
hold on
plot(x1,y);
function y=lglrcz(x0,y0,x)
n=length(x0);
m=length(x);
for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;
end
end

观察图像的左右两端,龙格现象十分明显,其数量级达到了10^18,可见如果要是再增大n值,数量级只能更大,所以无法满足题中条件。
4.有一形状较为复杂,但表面很光滑的曲面工件,通过科学手段,将其放置于某一空间坐标系下测得曲面上若干个点的坐标如下;
| z | y | |||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | ||
| x | -5 | 13.6 | -8.2 | -14.8 | -6.6 | 1.4 | 0 | -3.8 | 1.4 | 13.6 | 16.8 | 0 |
| -4 | -8.2 | -15.8 | -7.9 | 2.2 | 3.8 | 0 | 0.6 | 7.3 | 10.1 | 0 | -16.8 | |
| -3 | -14.8 | -7.9 | 2.5 | 5.8 | 2.3 | 0 | 2.7 | 5.1 | 0 | -10.1 | -13.7 | |
| -2 | -6.6 | 2.2 | 5.9 | 3.0 | -0.3 | 0 | 1.9 | 0 | -5.1 | -7.3 | -1.4 | |
| -1 | 1.4 | 3.8 | 2.3 | -0.3 | -0.9 | 0 | 0 | -1.7 | -2.7 | -0.6 | 3.8 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | -3.8 | 0.6 | 2.7 | 1.7 | 0 | 0 | 0.9 | 0.3 | -2.3 | -3.8 | -1.4 | |
| 2 | 1.4 | 7.3 | 5.1 | 0 | -1.7 | 0 | 0.3 | -3.1 | -5.8 | -2.2 | 6.6 | |
| 3 | 13.6 | 10.1 | 0 | -5.1 | -2.7 | 0 | -2.3 | -5.8 | -2.5 | 7.9 | 14.8 | |
| 4 | 16.8 | 0 | -10.1 | -7.3 | -0.6 | 0 | -3.8 | -2.2 | 7.9 | 15.8 | 8.2 | |
| 5 | 0 | 16.3 | -13.6 | -1.4 | 3.8 | 0 | -1.4 | 6.6 | 14.8 | 8.2 | -13.6 | |
要求:
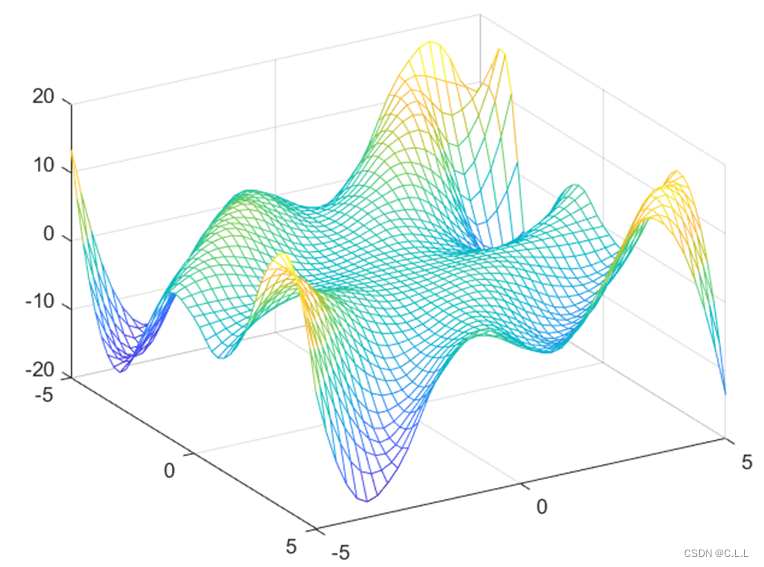
(1)画出该曲面工件的图形;
(2)在已知相邻的横、纵坐标之间分别插人三个分点,用interp2 命令计算出所有点处的竖坐标,画出相应的插值曲面;
(3)分别用不同的方法求出该曲面工件表面积的近似值.
(1)由于z的值太多且没有规律,我们将其复制到Excel表格中,并用matlab读取。
format long
clc;clear;
x=-5:5;
y=-5:5;
[x,y]=meshgrid(x,y);
z=xlsread('C:\Users\dell\Desktop\工件.xlsx');
figure(1)
mesh(x,y,z);
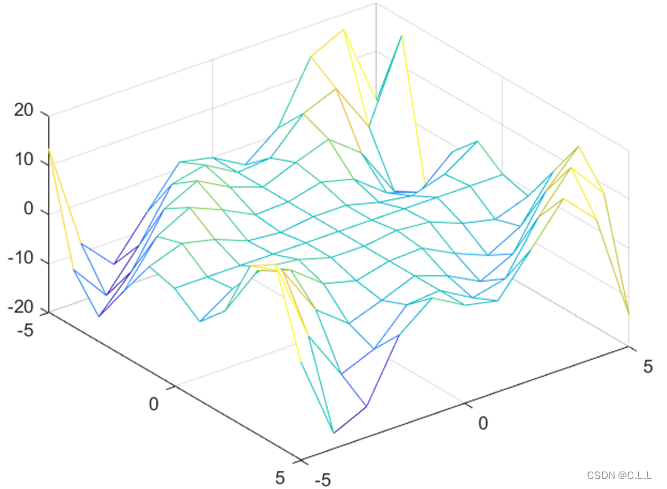
(2)原来有11个数据,相邻两个之间插入三个点后有41个数据。
format long
xx=linspace(-5,5,41);
[xx,yy]=meshgrid(xx,xx);
zz=interp2(x,y,z,xx,yy,'cubic');
mesh(xx,yy,zz);
(3)我们将图形分割成500*500个小网格,每个小网格当成矩形来计算:
format long
clc;clear;
x=-5:5;
y=-5:5;
[x,y]=meshgrid(x,y);
z=xlsread('C:\Users\dell\Desktop\工件.xlsx');
xx=linspace(-5,5,501);
[xx,yy]=meshgrid(xx,xx);
zz=interp2(x,y,z,xx,yy,'cubic');
s=0;
for i=1:500for j=1:500l1=sqrt((xx(i,j)-xx(i,j+1))^2+(yy(i,j)-yy(i,j+1))^2+(zz(i,j)-zz(i,j+1))^2);l2=sqrt((xx(i,j)-xx(i+1,j))^2+(yy(i,j)-yy(i+1,j))^2+(zz(i,j)-zz(i+1,j))^2);s=s+l1*l2;end
end
s
s = 3.349303482718335e+03
本文由作者自创,由于时间原因,难免出现些许错误,还请大家多多指正。创作不易,请大家多多支持。