迪杰斯特拉算法(Dijkstra's Algorithm):
由来:
迪杰斯特拉(Dijkstra)算法是由荷兰计算机科学家艾兹赫尔·戴克斯特拉(Edsger W. Dijkstra)在1956年提出的一种解决带权有向图中单源最短路径问题的算法。该算法采用贪心策略,逐步找到从源点到其余各个顶点的最短路径。
特点:
迪杰斯特拉算法的主要特点是从起始点开始,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。在算法执行过程中,通过不断更新距离值,逐步逼近最短路径的实际长度。
注意:
该算法要求图中不存在负权边,因为负权边可能导致贪心策略失效,无法得到正确的最短路径。此外,迪杰斯特拉算法只能求解单源最短路径问题,即给定一个源点,求该源点到图中其他所有点的最短路径。其时间复杂度通常为O(V^2),其中V是图中顶点的数量。如果使用优先队列等数据结构进行优化,可以降低时间复杂度。
具体操作(过程实现):
它的规则:
1.每次从未标记的节点中选择距离出发点最近的节点标记收录到最优路径集合中。
2.计算刚加入节点A的邻近节点B的距离(不包括标记的节点),若节点A的距离+节点A到B的边长<节点B的距离,就更新节点B的距离和前面点
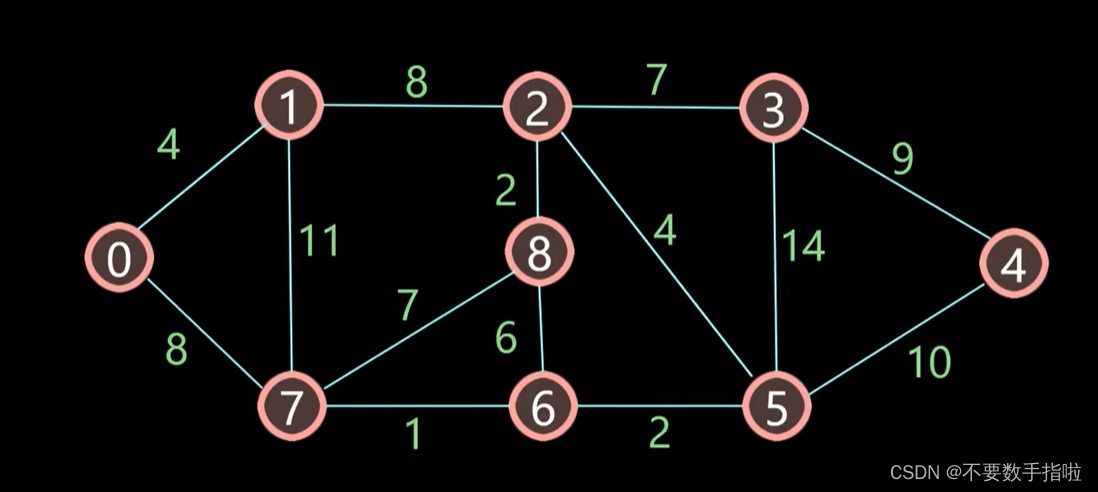
这个图,首先确定原点和终点,原点就是起始节点位置,终点是最后一个节点。它是一个带权无向图。假设是从0号位置走到4号位置的话。我们应该要关注三个点,首先是最短路径,其次是出发点和出发点前面一个节点,我们举例子:

以0开始的话,它可以走1号位置和7号位置,那么这个时候我们就可以给1号位置和7号位置的出发点赋上一个值。1的出发点赋值4,7的出发点值为8,前面节点我们就把0的节点填上去.
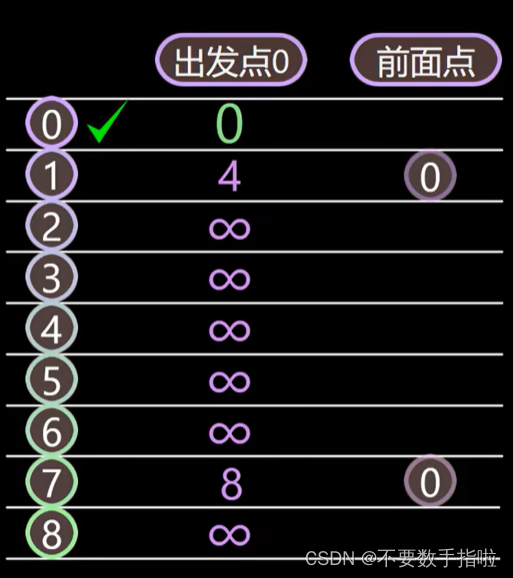
这个时候我们又可以继续往下看,在这一系列过程当中,出发点中只有1和7,还没有被标记,并且他们的出发点是有值的,这个时候我们可以发现出发点最小值是1位置的,我们就把1号位置也标记下来。标记下来之后,我们就以1号位置为初始点,继续往下找1号,位置所对应的有7号和2号这个时候我们可以发现从0到1到2号位置是4+8=12。这个时候我们就可以写上他的出发点的那个值赋上为12。然后还有7位置,我们算一下从0~1~7就是4+11=15, 15的是大于8,所以我们这个时候就不更新7号位置出发点的值,同时那个节点也不发生改变。但是2号位置的节点会改变,因为找到那个值了,就给他赋上去2号位置的前面一点,就是1号位置。
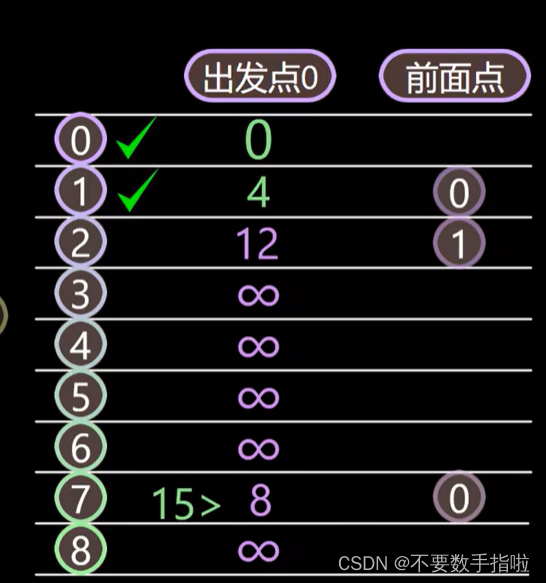
最后,层层推理结果为这幅图
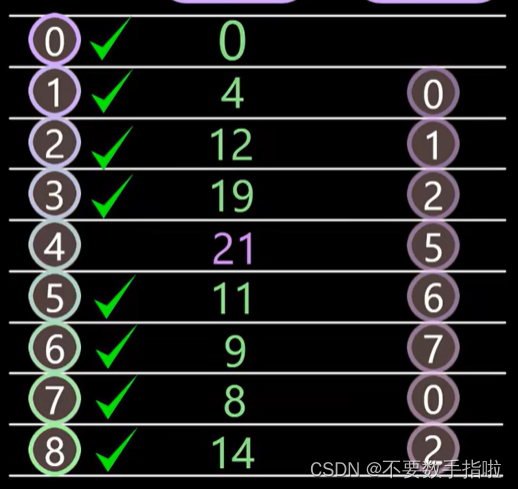
通过这个图我们可以知道,从0号位置到4号位置的权值为21。
这个时候我们可以推出他的路径,从4开始往前推,4的前一个点是5,5的前一个点是6,6的前一个点是7,7的前一个点是0,这个时候我们就推出来了,这条路是0->7->6->5->4.
算法的执行过程可以大致分为以下几个步骤:
- 初始化:设置一个集合S,用于存储已经找到最短路径的顶点,初始时只包含起始点;另一个集合U,用于存储尚未找到最短路径的顶点,初始时包含除起始点外的所有顶点。对于U中的每个顶点,记录其到起始点的距离,初始时这个距离就是顶点与起始点之间的边的权值,如果两个顶点之间没有边相连,则距离设为无穷大。
- 从U中选择一个距离起始点最近的顶点k,将其加入到S中,并从U中移除。
- 更新U中各个顶点到起始点的距离。对于U中的每个顶点u,如果通过顶点k到达u的路径比原来记录的路径更短,则更新u的距离值。具体来说,如果d(s, k) + d(k, u) < d(s, u),则更新d(s, u)为d(s, k) + d(k, u),其中d(s, k)表示起始点到顶点k的距离,d(k, u)表示顶点k到顶点u的距离,d(s, u)表示起始点到顶点u的距离。
- 重复步骤2和3,直到U为空,即所有顶点都已经被加入到S中,此时就找到了从起始点到所有其他顶点的最短路径。