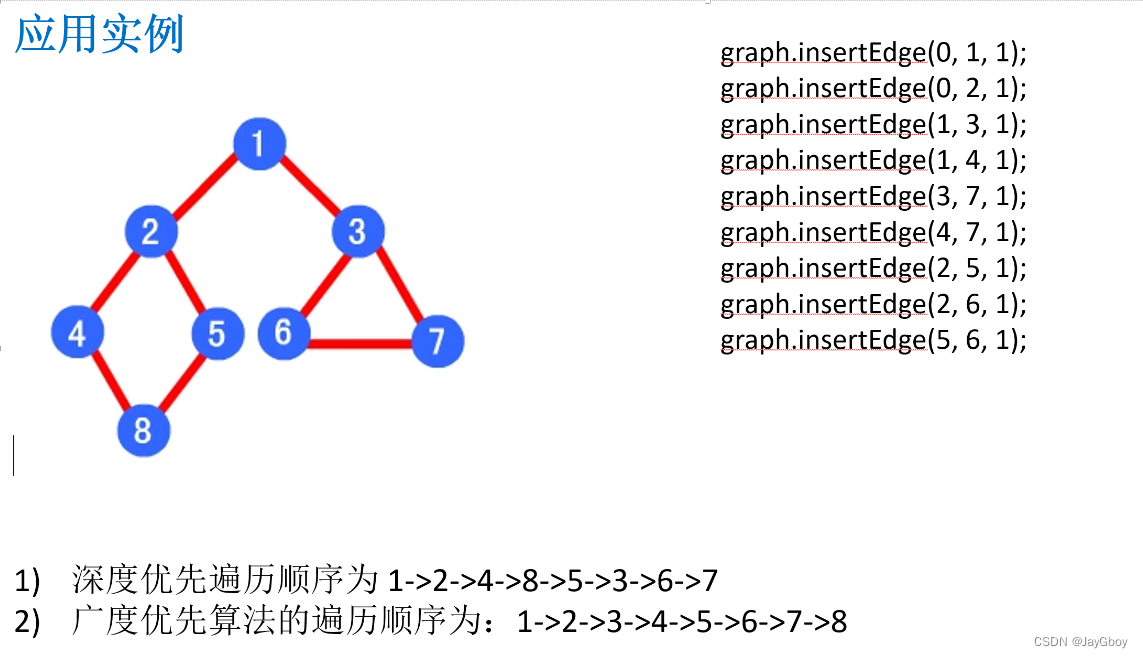
在数据结构中,图(Graph)是由节点(Vertex)和连接节点的边(Edge)组成的一种非线性数据结构。图可以用来表示各种实际问题中的关系和连接,如社交网络、道路网络、电路等。
图由两个主要部分组成:节点和边。节点表示实体或对象,而边表示节点之间的连接关系。图可以分为有向图(Directed Graph)和无向图(Undirected Graph)两种类型。在有向图中,边有方向,表示从一个节点到另一个节点的单向关系;而在无向图中,边没有方向,表示节点之间的双向关系。
图的常用代码实现方式有两种:邻接矩阵(Adjacency Matrix)和邻接表(Adjacency List)。
1. 邻接矩阵:
邻接矩阵是一个二维数组,用于表示图中节点之间的连接关系。如果图有 \(n\) 个节点,那么邻接矩阵就是一个大小为 \(n \times n\) 的矩阵。对于无向图,邻接矩阵是对称的;对于有向图,邻接矩阵可能不对称。邻接矩阵中的元素表示节点之间是否存在边,可以用 0 和 1 表示,或者用其他值表示边的权重。
例如,以下是一个无向图的邻接矩阵表示:
0 1 1 0
1 0 1 1
1 1 0 0
0 1 0 0
在邻接矩阵中,行号和列号对应于节点的标识符,矩阵中的元素表示对应节点之间是否存在边。
2. 邻接表:
邻接表是一种更紧凑的图表示方法,它使用一个数组和一组链表来表示图中的节点和边。数组的每个元素对应一个节点,而链表中的每个节点表示与该节点相邻的节点。
例如,以下是一个无向图的邻接表表示:
0 : [1, 2]
1 : [0, 2, 3]
2 : [0, 1]
3 : [1]
在邻接表中,数组的索引表示节点的标识符,链表中的元素表示与该节点相邻的节点。
这些是图的常用代码表示方法,选择哪种方法取决于具体的应用场景和操作需求。
当涉及到图的遍历时,常用的算法是深度优先搜索(Depth-First Search,DFS)和广度优先搜索(Breadth-First Search,BFS)。下面是它们的代码实现:
深度优先搜索(Depth-First Search,DFS):
def dfs(graph, start):visited = set() # 用集合来存储已访问的节点stack = [start] # 用栈来实现深度优先搜索while stack:vertex = stack.pop() # 从栈中弹出一个节点if vertex not in visited:print(vertex) # 访问该节点visited.add(vertex) # 将节点标记为已访问# 将该节点的邻接节点按逆序推入栈中for neighbor in reversed(graph[vertex]):if neighbor not in visited:stack.append(neighbor)
广度优先搜索(Breadth-First Search,BFS):
from collections import dequedef bfs(graph, start):visited = set() # 用集合来存储已访问的节点queue = deque([start]) # 用队列来实现广度优先搜索while queue:vertex = queue.popleft() # 从队列左侧弹出一个节点if vertex not in visited:print(vertex) # 访问该节点visited.add(vertex) # 将节点标记为已访问# 将该节点的邻接节点推入队列中for neighbor in graph[vertex]:if neighbor not in visited:queue.append(neighbor)