数学上，高斯消元法（或译：高斯消去法），是线性代数规划中的一个算法，可用来为线性方程组求解，其核心是：

1)两方程互换，解不变；
2)一方程乘以非零数k，解不变；
3)一方程乘以数k加上另一方程，解不变 。

一、高斯消元解线性方程组

1.题目描述

输入一个包含 n 个方程 n 个未知数的线性方程组。

方程组中的系数为实数。

求解这个方程组。

下图为一个包含 m 个方程 n 个未知数的线性方程组示例：

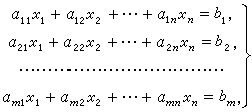
输入格式

第一行包含整数 n。

接下来 n 行，每行包含 n+1 个实数，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式

如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解，结果保留两位小数。

注意：本题有 SPJ，当输出结果为 0.00 时，输出 -0.00 也会判对。在数学中，一般没有正零或负零的概念，所以严格来说应当输出 0.00，但是考虑到本题作为一道模板题，考察点并不在于此，在此处卡住大多同学的代码没有太大意义，故增加 SPJ，对输出 -0.00 的代码也予以判对。

如果给定线性方程组存在无数解，则输出 Infinite group solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围

1≤n≤100,
所有输入系数以及常数均保留两位小数，绝对值均不超过 100。

输入样例：

3
1.00 2.00 -1.00 -6.00
2.00 1.00 -3.00 -9.00
-1.00 -1.00 2.00 7.00

输出样例：

1.00
-2.00
3.00

2.算法思路

1. 系数矩阵化为上三角矩阵：枚举每一列c

• 找到绝对值最大的一行
• 将该行与最上面一行（第一行）交换
• 将该行的第一个数变成1（该行同时除以该数）
• 将下面所有行的第c列变成0
• 在下一次进行操作时不需要再考虑这一行

2. 上三角矩阵化为对角矩阵：从后往前枚举对角线上的每一个1

• 用这个1消掉其他行的该列数
• 这个步骤可以省略，可以直接对最后一列常数列操作

3. 判断：

• 如果恰好化为对角矩阵，则有唯一一组解
• 如果最后一行稀疏矩阵全为0，但是最后的常数项不是0，则没有解
• 如果最后一行稀疏矩阵全为0，最后的常数项也是0，则无穷解

3.代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;const int N = 110;
const double eps = 1e-8;int n;
double a[N][N];int gauss()  // 高斯消元，答案存于a[i][n]中，0 <= i < n
{int c, r;for (c = 0, r = 0; c < n; c ++ ){int t = r;for (int i = r; i < n; i ++ )  // 找绝对值最大的行if (fabs(a[i][c]) > fabs(a[t][c]))t = i;if (fabs(a[t][c]) < eps) continue;for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);  // 将绝对值最大的行换到最顶端for (int i = n; i >= c; i -- ) a[r][i] /= a[r][c];  // 将当前行的首位变成1for (int i = r + 1; i < n; i ++ )  // 用当前行将下面所有的列消成0if (fabs(a[i][c]) > eps)for (int j = n; j >= c; j -- )a[i][j] -= a[r][j] * a[i][c];r ++ ;}if (r < n){for (int i = r; i < n; i ++ )if (fabs(a[i][n]) > eps)return 2; // 无解return 1; // 有无穷多组解}for (int i = n - 1; i >= 0; i -- )for (int j = i + 1; j < n; j ++ )a[i][n] -= a[i][j] * a[j][n];return 0; // 有唯一解
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ )for (int j = 0; j < n + 1; j ++ )scanf("%lf", &a[i][j]);int t = gauss();if (t == 2) puts("No solution");else if (t == 1) puts("Infinite group solutions");else{for (int i = 0; i < n; i ++ )printf("%.2lf\n", a[i][n]);}return 0;
}

二、高斯消元解异或线性方程组

1.题目描述

输入一个包含 n 个方程 n 个未知数的异或线性方程组。

方程组中的系数和常数为 0 或 1，每个未知数的取值也为 0 或 1。

求解这个方程组。

异或线性方程组示例如下：

M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]

其中 ^ 表示异或(XOR)，M[i][j] 表示第 i 个式子中 x[j] 的系数，B[i] 是第 i 个方程右端的常数，取值均为 0 或 1。

输入格式

第一行包含整数 n。

接下来 n 行，每行包含 n+1 个整数 0 或 1，表示一个方程的 n 个系数以及等号右侧的常数。

输出格式

如果给定线性方程组存在唯一解，则输出共 n 行，其中第 i 行输出第 i 个未知数的解。

如果给定线性方程组存在多组解，则输出 Multiple sets of solutions。

如果给定线性方程组无解，则输出 No solution。

数据范围

1≤n≤100

输入样例：

3
1 1 0 1
0 1 1 0
1 0 0 1

输出样例：

1
0
0

2.算法思路

思路与上一题完全一致，唯一区别在于运算不同，全部变为异或运算

1. 化为上三角矩阵的处理变成直接异或
2. 化为对角矩阵的处理变成异或另外两项相乘

3.代码

#include <iostream>
#include <algorithm>using namespace std;const int N = 110;int n;
int a[N][N];int gauss()
{int c, r;for (c = 0, r = 0; c < n; c ++ ){int t = r;for (int i = r; i < n; i ++ )if (a[i][c])t = i;if (!a[t][c]) continue;for (int i = c; i <= n; i ++ ) swap(a[r][i], a[t][i]);for (int i = r + 1; i < n; i ++ )if (a[i][c])for (int j = n; j >= c; j -- )a[i][j] ^= a[r][j];r ++ ;}if (r < n){for (int i = r; i < n; i ++ )if (a[i][n])return 2;return 1;}for (int i = n - 1; i >= 0; i -- )for (int j = i + 1; j < n; j ++ )a[i][n] ^= a[i][j] * a[j][n];return 0;
}int main()
{cin >> n;for (int i = 0; i < n; i ++ )for (int j = 0; j < n + 1; j ++ )cin >> a[i][j];int t = gauss();if (t == 0){for (int i = 0; i < n; i ++ ) cout << a[i][n] << endl;}else if (t == 1) puts("Multiple sets of solutions");else puts("No solution");return 0;
}