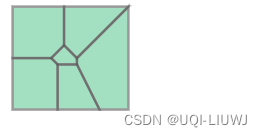
Voronoi 图是一种将平面分割成区域的方法，每个区域包含一个输入点，任何在该区域内的点都比其他输入点更接近该区域的输入点

1 基本使用方法

shapely.ops.voronoi_diagram(geom, envelope=None, tolerance=0.0, edges=False)

2 参数说明

geom	任何几何类型。几何体的所有顶点将被用作 Voronoi 图的输入点
edges	如果为 False，将返回一个多边形列表。否则，返回一个 LineString 边的列表

3 举例

from shapely.ops import voronoi_diagram
points = MultiPoint([(0, 0), (1, 1), (0, 2), (2, 2), (3, 1), (1, 0)])
points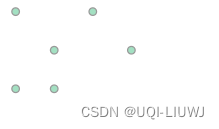

regions = voronoi_diagram(points)
regions