二叉搜索树——迭代实现-编程知识

二叉搜索树——迭代实现

————————————————————
普通的树形结构中数据是杂乱无章的，实际意义不大，要想更好的管理数据，需要让数据有序，二叉搜索树又称二叉排序树，是一种特殊的树形结构。
规定一般的二叉搜索树的左节点小于父节点，右节点大于父节点，节点均不相等
图例：
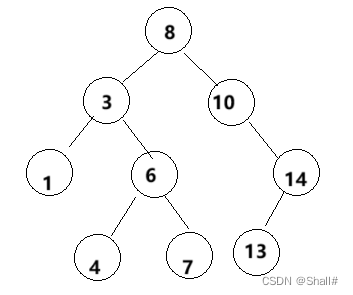
在这里插入图片描述

学习一种数据结构，自然要学会模拟实现它的增删查改啦，废话不多说，开始手撕搜索树吧。

（完整代码已放至gitee，按需参考，如有错误欢迎指出）

https://gitee.com/chxchenhaixiao/test_c/commit/4b77962a29e603679f9d21ecabdd87cb5a15e5e5

一、定义节点结构

这一步非常简单，不需要过多思考

template<class K>
struct BSTreeNode{K _key;BSTreeNode* left;BSTreeNode* right;BSTreeNode(K key):_key(key),left(nullptr),right(nullptr){}	//不要忘记写构造函数
};

二、定义搜索二叉树类

template<class K>
class BSTree{
private:	//protected:也可typedef BSTreeNode Node;//定义内部类型Node* _root=nullptr; //只需要存根节点//……
public://……
};

三、查找实现
也非常简单，严格遵守二叉搜索树特征

如果目标值小于当前值，左走
如果目标值大于当前值，右走
如果当前值为空，则找不到

bool Find(const K& key){Node* cur = _root;while(cur){if(key<cur->_Key)cur=cur->left;else if(key>cur->_key)cur=cur->right;elsereturn true;}return false;
}

四、插入实现

情形一：
当前节点数为0，直接更新_root即可
情形二：
当前节点数大于0，需要找到符合要求的位置

bool Insert(const K& key){Node* node = new Node(key);Node* prev=nullptr;	//需要记录前一个位置方便链接新节点Node* cur=_root;if(_root==nullptr)_root=node;else{while(cur){prev=cur;if(key<cur->_key)cur=cur->left;else if(key>cur->right)cur=cur->right;}elsereturn false;//if(prev->left==cur)prev->left=node;elseprev->right=node;/*这一步很重要，一定要进行判断所找到的空节点是在prev的左还是右*/}return true;
}

五、删除实现
删除的情形可以分为三种：
1、目标节点为叶子节点：
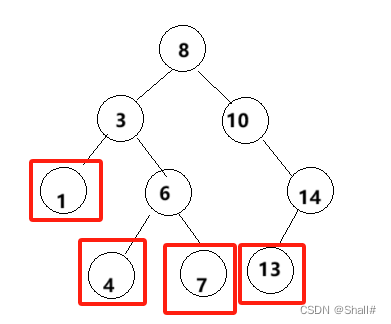
在这里插入图片描述
2、目标节点只有单个孩子节点：

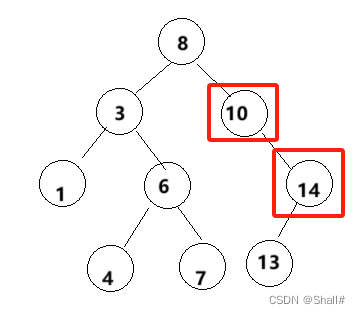
3、目标节点左右孩子均存在：

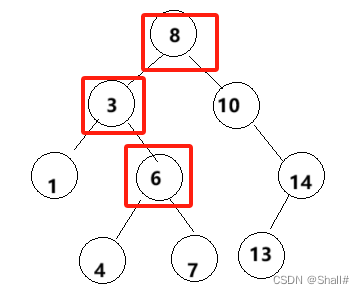
针对不同的情形，要采取不同的方式

对于第一种情况，只需要将目标节点的父节点中的一个指针置为空
对于第二种情况，需要将目标节点的孩子节点交给父节点

加入把空指针也算作一个节点，那么前两种情形即可归并为一类

对于第三种情况，不能像前两种一样了，而是需要寻找目标节点右（左）子树的最小（大）节点与目标节点交换，再将问题转变为前两种情形

bool Erase(const K& key) {if (Find(key) == false)return false;Node* cur = _root;Node* prev = nullptr;while (key != cur->_key) {prev = cur;if (key < cur->_key) {cur = cur->left;}else {cur = cur->right;}}if (cur->left == nullptr) {if (prev == nullptr) {_root = cur->right;}else {if (prev->left == cur) {prev->left = cur->right;}else {prev->right = cur->right;}}delete cur;}else if (cur->right == nullptr) {if (prev == nullptr) {_root = cur->left;}else {if (prev->left == cur) {prev->left = cur->left;}else {prev->right = cur->left;}}delete cur;}else {Node* MinRight = cur->right;Node* pMinRight = cur;while (MinRight->left) {pMinRight = MinRight;MinRight = MinRight->left;}cur->_key = MinRight->_key;if (pMinRight->left == MinRight)pMinRight->left = MinRight->right;else {pMinRight->right = MinRight->right;}delete MinRight;}return true;}

几个易错点：
1、
在这里插入图片描述
不要忘记这里的判断，如果没有这一句，
当删除一颗歪脖树的根节点会崩溃

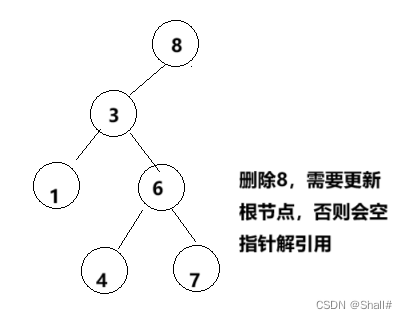
2、

pMinRight的初值不可以为空

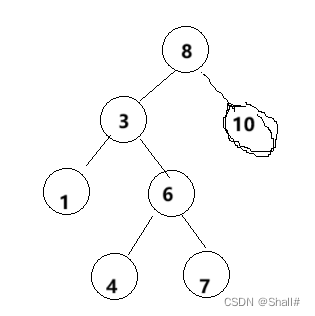
否则删除10时，pMinRight不会得到更新，会导致运行崩溃
3、

这里的判断少不得，可以不要以为目标节点的右子树一定是链接在父节点的左边
也许目标节点的父节点是根节点
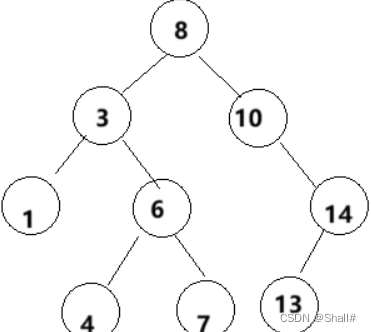
在这里插入图片描述
（删除8时就需要将10的右树链接在pMinRight右）