这是树的第22篇算法,力扣链接。
给你一棵二叉树的根节点
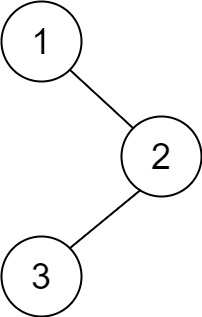
root,返回其节点值的 后序遍历 。示例 1:
输入:root = [1,null,2,3] 输出:[3,2,1]
我们来回忆一下后续遍历逻辑:
后序遍历 (Postorder Traversal)
后序遍历的顺序是:
- 遍历左子树
- 遍历右子树
- 访问根节点
后序遍历常用于删除或释放树中的节点。因为你在删除节点之前先访问其子节点,这样可以安全地删除每个节点。
例子
假设有一棵二叉树如下:
A/ \B C/ \ \ D E F
- 后序遍历:
D, E, B, F, C, A。首先是左子树(D, E, B),然后是右子树(F, C),最后是根节点(A)。
后续遍历会优先去到最左节点,然后一点一点往回走。
func postorderTraversal(root *TreeNode) []int {var result []intif root == nil {return result}var (stack []*TreeNodeprev *TreeNode)for root != nil || len(stack) > 0 {for root != nil {stack = append(stack, root)root = root.Left}node := stack[len(stack)-1]if node.Right == nil || node.Right == prev {result = append(result, node.Val)prev = nodestack = stack[:len(stack)-1]} else {root = node.Right}}return result
}
递归写法:
func postorderTraversal(root *TreeNode) []int {var result []intvar postorder func(*TreeNode)postorder = func(node *TreeNode) {if node == nil {return}postorder(node.Left)postorder(node.Right)result = append(result, node.Val)}postorder(root)return result
}