在这篇文章中我将讨论用于树和图的两种遍历机制之一。将使用 C# 示例介绍广度优先搜索 (BFS)。图是最具挑战性和最复杂的数据结构之一。
广度优先搜索的工作原理:广度优先搜索 (BFS)是一种探索树或图的方法。在 BFS 中,您首先探索一步之外的所有节点,然后探索两步之外的所有节点,依此类推。
如果我们熟悉广度优先搜索,那么理解系统设计概念和破解面试问题就会很容易。
广度优先搜索就像向池塘中心扔一块石头。您探索的节点从起点“产生涟漪”。
以下是 BFS 从根开始遍历这棵树的方式:
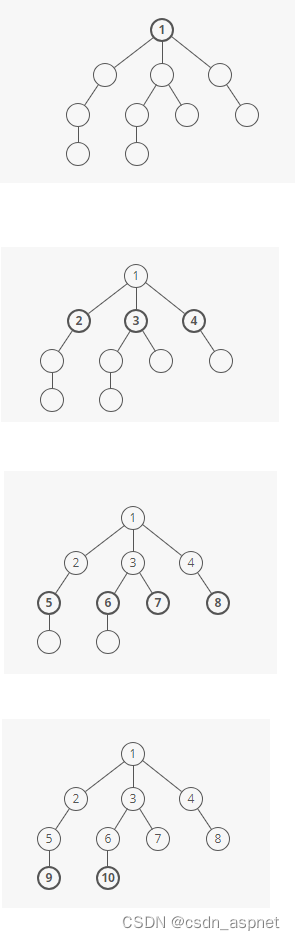
广度优先优先遍历树
在上图的第一张图中,我们从最顶层的节点开始。
在第二张图中,我们遍历第二层存在的所有节点。在第三张图像中,所有节点都出现在第三层,依此类推。直到我们到达终点。
优点:
BFS 将找到 起点和任何其他可到达节点之间的最短路径。深度优先搜索不一定能找到最短路径。
缺点:
二叉树上的 BFS 通常 比 DFS 需要更多的内存。
示例一:
广度优先搜索代码示例
在下面的代码中,我尝试创建与下图所示相同的结构。
static void Main(string[] args)
{
IDictionary> tree = new Dictionary>();
tree[1] = new List { 2, 3, 4 };
tree[2] = new List { 5 };
tree[3] = new List { 6, 7 };
tree[4] = new List { 8 };
tree[5] = new List { 9 };
tree[6] = new List { 10 };
HashSet itemCovered = new HashSet();
Queue queue = new Queue();
queue.Enqueue(tree.ElementAt(0).Key);
while (queue.Count > 0)
{
var element = queue.Dequeue();
if (itemCovered.Contains(Convert.ToInt32(element)))
continue;
else
itemCovered.Add(Convert.ToInt32(element));
Console.WriteLine(element);
List neighbours;
tree.TryGetValue(Convert.ToInt32(element), out neighbours);
if (neighbours == null)
continue;
foreach (var item1 in neighbours)
{
queue.Enqueue(item1);
}
}
}
}
我正在上面的代码中执行以下步骤来遍历树:
首先水平移动,访问当前层的所有节点
移动到下一层
我正在使用队列来推送正在遍历的项目,并将该项目的所有邻居添加到队列中。一旦遍历将它们弹出。
上述代码的输出如下图所示:

广度优先搜索问题:
给定 root 二叉树的 ,返回 树 中每一行中最大值的数组(从 0 开始索引)。
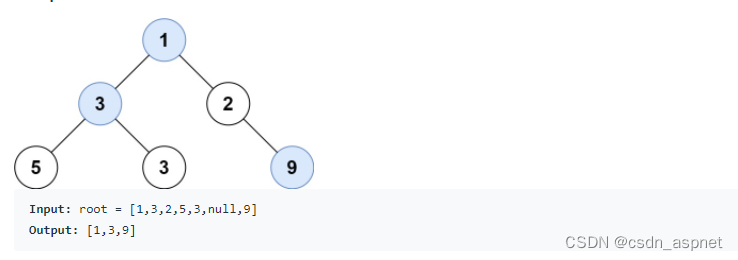 解决方案:
解决方案:
作为解决方案的一部分,我们将遍历一级的所有节点并尝试找到最大节点。
1、将根节点添加到队列中。
2、遍历队列,直到队列为空。
3、获取队列中元素的数量。
4、遍历元素直到计数为止。
5、获取内循环中的最大值。
public int[] FindLargestValueinEachTreeRowMethod(TreeNode root)
{
List<int> result = new List<int>();
if (root == null) return result.ToArray();
Queue dfs_queue = new Queue();
dfs_queue.Enqueue(root);
while (dfs_queue.Count > 0)
{
int max_value = Int32.MinValue;
int elements_count = dfs_queue.Count;
for (int i = 0; i <= elements_count; i++)
{
TreeNode node = dfs_queue.Dequeue();
max_value = Math.Max((int)max_value, (int)node.val);
if (node.left != null) dfs_queue.Enqueue(node.left);
if (node.right != null) dfs_queue.Enqueue(node.right);
}
result.Add(max_value);
}
return result.ToArray();
}
广度优先搜索的实际应用:
我被问到一个与 BFS 相关的非常有用且有趣的编程面试问题。下面是问题。
给你一张地铁站的网格图,编写一个函数来输出从每个路口到最近车站的距离。从一个点到另一个点时,你不能沿对角线移动。答案有点复杂,但也不是很难。
输入:
。。。。。X
。。。。。。
。。。。。。
。X 。。。。
。。。。X 。
输出:
4 3 3 2 1 0 3
2 3 3
2 1 2 1 2 3 2
2 1 0 1 2 1 2
2 1 2 1 0 1
示例二:
图是数据结构和算法中非常重要的话题
class BfsGraph
{
LinkedList<int>[] _adj;
int _V;
public BfsGraph(int v)
{
_adj = new LinkedList<int>[v];
for (int i = 0; i < v; i++)
{
_adj[i] = new LinkedList<int>();
}
_V = v;
}
public void AddEdge(int v, int w)
{
_adj[v].AddLast(w);
}
public void BFS(int v)
{
Queue<int> q = new Queue<int>();
bool[] flag = new bool[_V];
q.Enqueue(v);
flag[v] = true;
Console.WriteLine(v);
while (q.Count > 0)
{
int w = q.Dequeue();
LinkedList<int> linledList = _adj[w];
LinkedListNode<int> currentNode = linledList.First;
while (currentNode != null && !flag[currentNode.Value])
{
Console.WriteLine(currentNode.Value);
q.Enqueue(currentNode.Value);
flag[currentNode.Value] = true;
currentNode = currentNode.Next;
}
}
}
}
上面的 C# 代码定义了一个名为 BfsGraph 的类,它表示图数据结构并实现广度优先搜索 (BFS) 算法。该类有两个实例变量:_adj(表示图的邻接列表的 LinkedList<int> 对象数组)和 _V(表示图中顶点数的 int)。
BfsGraph 构造函数采用 int 参数 v 表示图中的顶点数。它使用大小为 v 的 LinkedList<int> 对象的新数组初始化 _adj 数组,并将 _V 的值设置为 v。构造函数还使用新的 LinkedList<int> 对象初始化 _adj 数组的每个元素。
AddEdge 方法采用两个 int 参数 v 和 w,表示图中的两个顶点。它通过将 w 添加到链表末尾 _adj 数组中索引 v 处来在这两个顶点之间添加一条边。
BFS 方法采用一个 int 参数 v 表示 BFS 遍历的起始顶点。它创建一个新的 Queue<int> 对象来存储要访问的顶点,并创建一个新的 bool[] 数组来跟踪已访问的顶点。该方法将起始顶点 v 排入队列,将标志数组中的相应元素设置为 true,并使用 Console.WriteLine 输出其值。
然后该方法进入一个循环,一直持续到队列为空为止。在每次迭代中,它都会从队列中出列一个顶点,从 _adj 数组中检索其邻接列表,并使用 while 循环迭代其元素。对于邻接列表中的每个未访问的顶点,它使用 Console.WriteLine 输出其值,将其排队并将其在标志数组中的相应元素设置为 true。
下面的示例演示了如何使用此类创建具有 4 个顶点的图,并从顶点 2 开始执行 BFS 遍历:
var graph = new BfsGraph(4);
graph.AddEdge(0, 1);
graph.AddEdge(0, 2);
graph.AddEdge(1, 2);
graph.AddEdge(2, 0);
graph.AddEdge(2, 3);
graph.AddEdge(3, 3);
Console.WriteLine("Breadth First Traversal starting from vertex 2:");
graph.BFS(2);
此代码创建具有 4 个顶点的 BfsGraph 类的新实例,使用 AddEdge 方法在它们之间添加边,并使用 BFS 方法从顶点 2 开始执行 BFS 遍历。该代码的输出将是:
从顶点开始广度优先遍历 2:
2
0
3
1
时间复杂度:O(v+e),其中 v 是节点数,e 是边数。
辅助空间:O(v)