原题链接:F2. Omsk Metro (hard version)
题目大意:
最初开始时,你有一个根节点 1 1 1 且权值为 1 1 1 。
接下来会有 n n n 个操作,每次操作按照如下格式给出:
设操作开始前节点总数为 c n t cnt cnt:
- + + + v v v x x x ,增加一个编号为 c n t + 1 cnt+1 cnt+1 ,且权值为 x ∈ { − 1 , 1 } x\in\{-1,1\} x∈{−1,1} 的节点,同时和节点 v v v 连上一条边(保证节点 v v v 存在)。
- ? ? ? x x x y y y k k k ,询问从 x x x 到 y y y 的路径上,是否可以从某个位置开始,选出一些连续节点,并且使得点权之和为 k k k 。
解题思路:
注意到形成的结构是一棵树,并且还有一个性质: x ∈ { − 1 , 1 } x\in\{-1,1\} x∈{−1,1} 。
我们引入一个结论:如果一个区间的和 s u m ≥ 0 sum\geq 0 sum≥0 ,那么我们可以通过删除最左边或最右边的一些元素,获得所有在区间 [ 0 , s u m ] [0,sum] [0,sum] 内的值,同样的, s u m ≤ 0 sum \leq 0 sum≤0 也满足这个条件。
感性证明一下为什么是对的:
首先我们肯定要从序列的一边慢慢删数,否则就不连续了。
- 下面只考虑 s u m ≥ 0 sum \geq 0 sum≥0 的情况, s u m ≤ 0 sum\leq0 sum≤0 的情况也同理。
- 假设序列的元素全为 1 1 1 ,结论显然是正确的。
- 假设序列包含至少一个 − 1 -1 −1 ,又因为 s u m = a × ( − 1 ) + b × 1 sum = a \times(-1)+b\times1 sum=a×(−1)+b×1 ,对于每一个 − 1 -1 −1,我们一定都能和某一个正 1 1 1 抵消掉这个 − 1 -1 −1 的贡献,即删除了这个 − 1 -1 −1 再删除一个 1 1 1 ,会使得 s u m sum sum 值不变,我们发现 − 1 -1 −1 的存在本质上是没有意义的,这样问题就转化成了序列元素全是 1 1 1 的情况了。
引入这个结论有什么用呢?
假设我们可以知道这个序列 最小的负值和 S 1 S_{1} S1 以及 最大的正值和 S 2 S_{2} S2 ,按照这个结论,我们一定能用 S 1 S_{1} S1 凑出 [ S 1 , 0 ] [S_{1}, 0] [S1,0] 的任意值,用 S 2 S_{2} S2 凑出 [ 0 , S 2 ] [0,S_{2}] [0,S2] 的任意值。
所以判断是否能选出一个子数组,使得和为 k k k ,即判断 S 1 ≤ k ≤ S 2 S_{1} \leq k \leq S_{2} S1≤k≤S2 即可。
回到这题上,能否在 x → y x \rightarrow y x→y 路径形成的序列上凑成 k k k ,本质就转化成了求 x → y x \rightarrow y x→y 路径的最小子段和,以及最大子段和,这是一个典型问题。
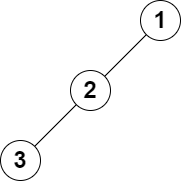
假设根为 1 1 1 ,我们要求 x → y x \rightarrow y x→y 的路径。
设 l c a lca lca 为 x , y x,y x,y 的最近公共祖先。
假设 l c a lca lca 是 x , y x,y x,y 的其中一个,那么答案就直接是 x → y x \rightarrow y x→y 路径上的最大 / / /小子段和。
否则就是 x → l c a x \rightarrow lca x→lca 和 l c a → y lca \rightarrow y lca→y 的路径拼起来,考虑怎么拼起来。
我们维护 7 7 7 个信息:
- 严格包含 区间最左 / / /右端点的最大子段和: m x l , m x r mxl,mxr mxl,mxr
- 严格包含 区间最左 / / /右端点的最小子段和: m n l , m n r mnl,mnr mnl,mnr
- 只看这个区间内部的最大 / / /小子段和: m x s u m , m n s u m mxsum,mnsum mxsum,mnsum
- 区间的和: s u m sum sum
假设我们已经知道 a → b a \rightarrow b a→b 和 b → c b \rightarrow c b→c 的信息,我们要怎么将这两个区间合并成 a → c a \rightarrow c a→c 的信息:
注意,这里的 a → b a \rightarrow b a→b 指的是 左闭右开区间 [ a , b ) [a,b) [a,b) ,转化为下标可以理解为闭区间 [ a , b − 1 ] [a,b-1] [a,b−1]。

下面只考虑最大子段和,最小子段和也是同理:
按照上图将 a → b a \rightarrow b a→b 统称为左边, b → c b \rightarrow c b→c 统称为右边。
-
m x s u m a → c = max { m x s u m a → b , m x s u m b → c , m x r a → b + m x l b → c } mxsum_{a \rightarrow c}=\max\{mxsum_{a \rightarrow b},mxsum_{b \rightarrow c}, mxr_{a \rightarrow b}+mxl_{b \rightarrow c}\} mxsuma→c=max{mxsuma→b,mxsumb→c,mxra→b+mxlb→c}
( a → c a \rightarrow c a→c 的最大子段和 m x s u m mxsum mxsum ,要么是左边或者右边其一的最大子段和,要么是左边 m x r mxr mxr 和右边 m x l mxl mxl 拼起来的中间那一段的和) -
m x r a → c = max { m x r b → c , m x r a → b + s u m b → c } mxr_{a \rightarrow c}=\max\{mxr_{b \rightarrow c},mxr_{a \rightarrow b}+sum_{b \rightarrow c}\} mxra→c=max{mxrb→c,mxra→b+sumb→c}
( a → c a \rightarrow c a→c 包含右端点的最大子段和 m x r mxr mxr,要么是右边的 m x r mxr mxr,要么是左边的 m x r mxr mxr 再加上右边一整段区间的和) -
m x l a → c = max { m x l b → c , s u m a → b + m a x l b → c } mxl_{a \rightarrow c}=\max\{mxl_{b \rightarrow c},sum_{a \rightarrow b}+maxl_{b \rightarrow c}\} mxla→c=max{mxlb→c,suma→b+maxlb→c}
( a → c a \rightarrow c a→c 包含左端点的最大子段和 m x l mxl mxl,要么是左边的 m x l mxl mxl,要么是左边一整段区间的和再加上右边的 m x l mxl mxl) -
s u m a → c = s u m a → b + s u m b → c sum_{a \rightarrow c} = sum_{a \rightarrow b} + sum_{b \rightarrow c} suma→c=suma→b+sumb→c
( a → c a \rightarrow c a→c 的区间的和直接就是左边的和和右边的和相加)
这样,我们就可以将树的每一条链分段维护,然后对每一段进行如上的信息合并,就能够实时求出 a → b a \rightarrow b a→b 这一整条链上的信息了。
对于这一题而言,我们可以用倍增表做到在线加点维护信息,在线询问。
注意到我们的信息是自底向上维护的,且询问区间是 [ x , y ) [x,y) [x,y) 的左闭右开区间,因此我们除了 l c a lca lca 是 x , y x,y x,y 的其中一个的情况,我们询问的答案都是 [ x , l c a ) , [ y , l c a ) [x,lca),[y,lca) [x,lca),[y,lca) 的信息。
这时我们要翻转一下一个区间,变成 [ x , l c a ) + [ l c a ] + ( l c a , y ] [x,lca)+[lca]+(lca,y] [x,lca)+[lca]+(lca,y] 的信息,才是 [ x , y ] [x,y] [x,y] 的信息。
细节比较多,可以看代码注释。
时间复杂度: O ( n log n ) O(n \log n) O(nlogn)
AC代码:
#include <bits/stdc++.h>
#define YES return void(cout << "Yes\n")
#define NO return void(cout << "No\n")
using namespace std;using u64 = unsigned long long;
using PII = pair<int, int>;
using i64 = long long;//这里是我们的信息结构体
struct Info {int mnl, mnr, mxl, mxr, sum;int mxsum, mnsum;Info() { mnl = mnr = mxl = mxr = sum = mxsum = mnsum = 0; };Info(int _) {//初始时全为 0mnl = mnr = mxl = mxr = sum = mxsum = mnsum = 0;//分类讨论点 u 权值为 > 0 和 < 0 的情况if (_ > 0) {mxl = mxr = sum = mxsum = _;} else {mnl = mnr = sum = mnsum = _;}}//维护最大子段和friend Info merge(const Info& a, const Info& b) {Info res;res.mxsum = max({ a.mxsum, b.mxsum, a.mxr + b.mxl });res.mnsum = min({ a.mnsum, b.mnsum, a.mnr + b.mnl });res.mxl = max(a.mxl, a.sum + b.mxl);res.mxr = max(b.mxr, a.mxr + b.sum);res.mnl = min(a.mnl, a.sum + b.mnl);res.mnr = min(b.mnr, a.mnr + b.sum);res.sum = a.sum + b.sum;return res;}//区间反转操作void reverse() {swap(mnl, mnr);swap(mxl, mxr);}
};void solve() {int n;cin >> n;const int logn = __lg(n);vector<vector<int>> nxt(n + 2, vector<int>(logn + 1));vector<vector<Info>> pre(n + 2, vector<Info>(logn + 1));vector<int> dep(n + 2);vector<tuple<int, int, int>> ask;//这里懒得把代码改了,就离线了,本质上是可以做到在线的int Node = 1;pre[Node][0] = Info(1);char op; int u, v, k;for (int i = 1; i <= n; ++i) {cin >> op >> u >> v;if (op == '+') {nxt[++Node][0] = u;dep[Node] = dep[u] + 1;pre[Node][0] = Info(v);} else {cin >> k;ask.emplace_back(u, v, k);}}//对每个点跳 2^j 步的信息都做一个如上的合并//注意信息是 [x, y) 的信息for (int j = 1; j <= logn; ++j) {for (int i = 1; i <= Node; ++i) {nxt[i][j] = nxt[nxt[i][j - 1]][j - 1];pre[i][j] = merge(pre[i][j - 1], pre[nxt[i][j - 1]][j - 1]);}}//求 LCA 模板auto LCA = [&](int u, int v) {if (dep[u] < dep[v]) swap(u, v);for (int j = logn; j >= 0; --j) {if (dep[u] - (1LL << j) >= dep[v]) {u = nxt[u][j];}}if (u == v) return u;for (int j = logn; j >= 0; --j) {if (nxt[u][j] != nxt[v][j]) {u = nxt[u][j];v = nxt[v][j];}}return nxt[u][0];};//cal函数 就是通过倍增计算 [x, a) + [a, b) + ... + [z, lca) 的信息从而得到 [x, lca) 的信息//特别要注意的是如果 u == lca 会返回一个全为 0 的信息,不会对答案产生影响,具体看代码即可明白原因auto cal = [&](int u, int lca) {Info res;for (int j = logn; j >= 0; --j) {if (dep[u] - (1LL << j) >= dep[lca]) {res = merge(res, pre[u][j]);u = nxt[u][j];}}return res;};//处理每个离线出来的询问for (auto [u, v, k] : ask) {int lca = LCA(u, v);Info A = cal(u, lca), B = cal(v, lca);A = merge(A, pre[lca][0]); //将 [u, lca) + [lca, lca]A.reverse(); //翻转 [u, lca]Info T = merge(B, A); //合并 [v, lca) + [lca, u];if (T.mnsum <= k && k <= T.mxsum) {cout << "Yes\n";} else {cout << "No\n";}}
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int t = 1; cin >> t;while (t--) solve();return 0;
}



![[NOIP2011 普及组] 数字反转](https://img-blog.csdnimg.cn/direct/29abc83666914b5f8579b24fc746fbc9.png)