一、树的概念
逻辑结构:层次结构,一对多
- 节点:树中的一个数据元素
- 根节点:树中的第一个节点,没有父节点
- 孩子节点:该节点的直接下级节点
- 父(亲)节点:该结点的直接上级节点
- 兄弟节点:有相同父亲节点的
- 祖先节点:该结点的间接上级节点
- 子孙节点:该结点的间接下级节点
- 堂兄弟节点:有相同的祖先节点,在树的同一层的节点
- 树的深度:取树中层次的最大值
- 节点的度:子节点的个数/分支个数
- 树的度:节点度的最大值
- 森林:多个树(大于等于2)
- 节点的深度:从根节点开始向下的层次

二、 二叉树
节点的度最大为2
严格区分左右子树
1.二叉树的概念
- 二叉树的度:最大为2
- 左子树:节点左侧的子树
- 右子树:节点右侧的子树
- 满二叉树:除了叶子节点外,每一个节点的度都为0,叶子节点只能在最后一层
- 叶子节点:度为0的节点
- 完全二叉树:可以由满二叉树从右侧删除子树得到
2.二叉树的五种形态

3.二叉树的性质
第n层上最多有:2^(n-1)
前n层上:2^n-1
二叉树的总节点数:总度数+1 (其中+1,加的是头节点)

4.二叉树的遍历
先序:根左右
中序:左根右
后序:左右根
练习1(一只一棵树的中序遍历和其他两种中任意一种,即可画唯一的二叉树)
先序:ABDGHCEFI 中序:GDHBAECIF
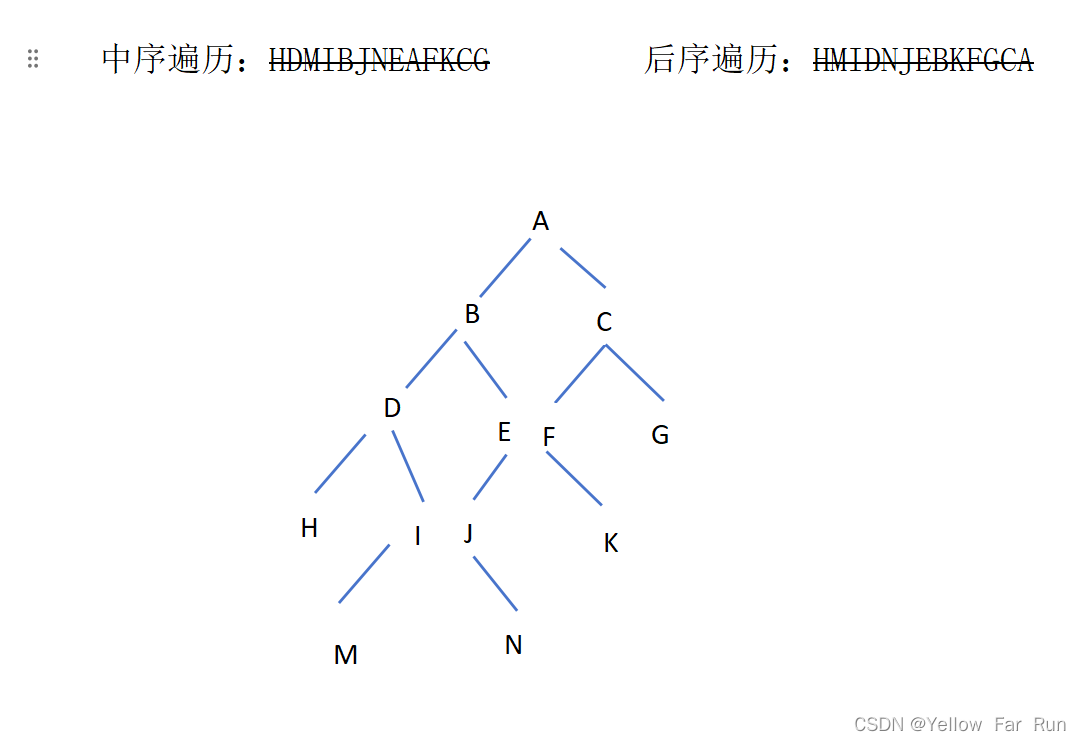
练习2.
中序遍历:HDMIBJNEAFKCG 后序遍历:HMIDNJEBKFGCA
三、功能
二叉树的结构体
#ifndef __TREE_H__
#define __TREE_H__
#include <stdio.h>
#include <stdlib.h>typedef struct tree_node{char data;struct tree_node *lchild;//左孩子struct tree_node *rchild;//右孩子
}tree,*tree_p;//创建节点的函数
tree_p creat_node(char data);
//创建二叉树(创建节点,再创建节点的左右子树)
//二叉树的左右子树,仍然是一个二叉树
tree_p creat_tree();
//先序遍历:根左右
void pri(tree_p T);
//中序遍历:左根右
void zx(tree_p T);
//后序遍历:左右根
void hx(tree_p T);#endif1.创建节点
//创建节点的函数
tree_p creat_node(char data){tree_p new=(tree_p)malloc(sizeof(tree));if(new==NULL){printf("申请空间失败\n");return NULL;}new->data=data;return new;
}2.创建二叉树
//创建二叉树(创建节点,再创建节点的左右子树)
//二叉树的左右子树,仍然是一个二叉树
tree_p creat_tree(){char data='\0'; //定义一个char类型的变量初始化为'\0'//不然data就是一个随机值,防止随机为#scanf("%c",&data);getchar();//吸收垃圾字符if(data=='#'){ //#为停止字符return NULL;}tree_p T=creat_node(data);//创建根节点T->lchild=creat_tree(); //左子数仍然是一个子树T->rchild=creat_tree();return T;
}3.先序遍历
//先序遍历:根左右
void pri(tree_p T){if(T==NULL){return;}printf("%c->",T->data);pri(T->lchild);//给根节点的左孩子调用先序遍历pri(T->rchild);//给根节点的右孩子调用先序遍历
}4.中序遍历
//中序遍历:左根右
void zx(tree_p T){if(T==NULL){return;}zx(T->lchild);printf("%c->",T->data);zx(T->rchild);
}5.后序遍历
//后序遍历:左右根
void hx(tree_p T){if(T==NULL){return;}hx(T->lchild);hx(T->rchild);printf("%c->",T->data);
}