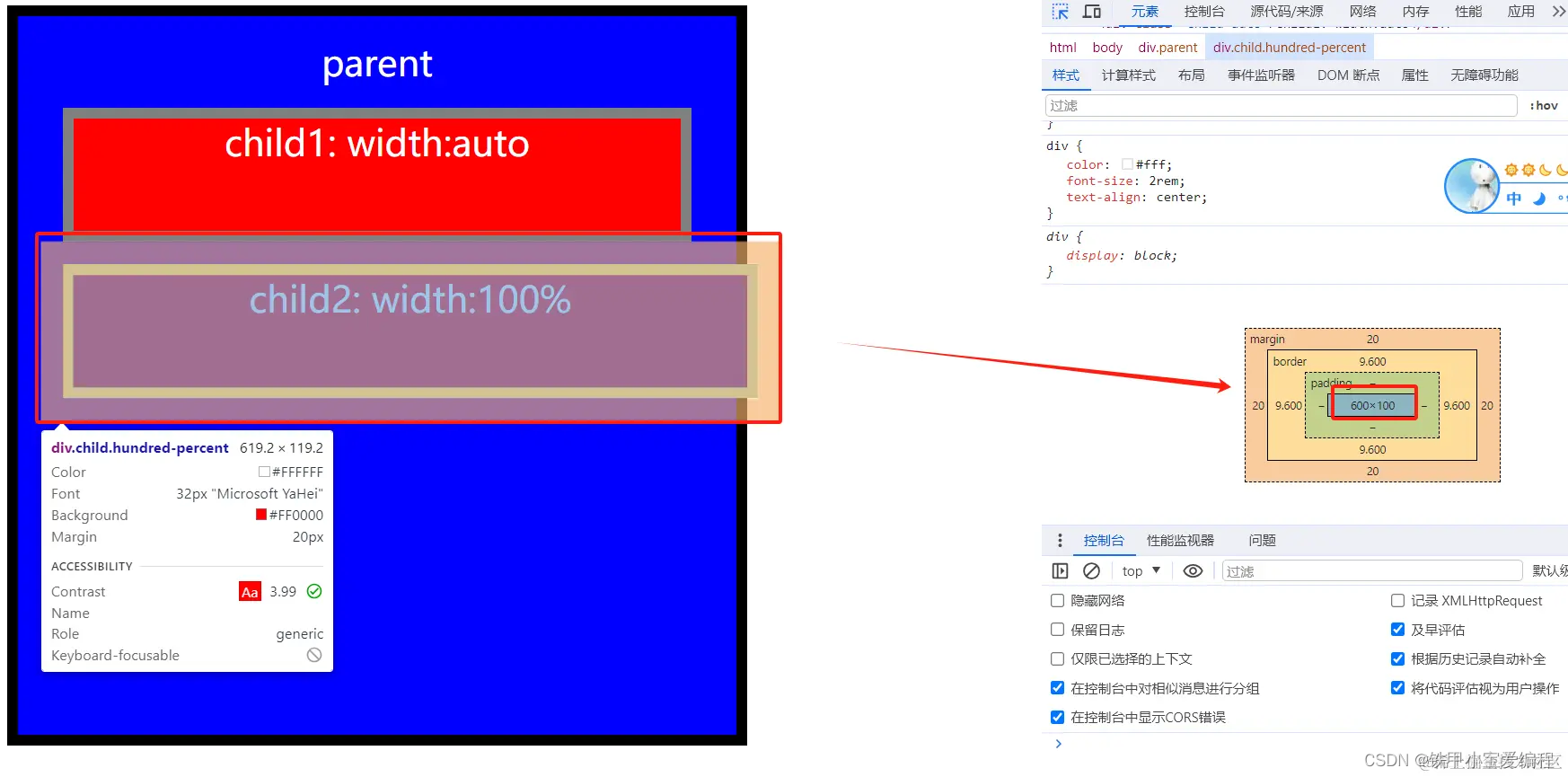
Function

这是一道很直观的递归题目，但是使用递归会导致时间超限，所以需要使用记忆化搜素。
首先把坑点讲一下：出题人会给出负数，而我们知道数组下标是不能有负数的，如果是二维数组还可以用map数组进行储存，但是这个函数是有三个变量，所以就只能使用三维数组了，这也就意味着在dfs函数的最前面我们需要进行特判，看这个数组下标是否处于正数，如果是正数我们就直接返回数组的值，如果是负数那么我们就用递归来搞定。

代码如下：

#include<iostream>
#include<cstdio>
#include<stdlib.h>using namespace std;
typedef  long long ll;
ll wa[40][40][40];
ll w(ll a,ll b,ll c)
{if(a<=20&&b<=20&&c<=20&&a>=0&&b>=0&&c>=0)if(wa[a][b][c]){return wa[a][b][c];}if(a<=0||b<=0||c<=0)return 1;if(a>20||b>20||c>20)return w(20,20,20);if(a<b&&b<c)return wa[a][b][c]=w(a,b,c-1)+w(a,b-1,c-1)-w(a,b-1,c);return wa[a][b][c]=w(a-1,b,c)+w(a-1,b-1,c)+w(a-1,b,c-1)-w(a-1,b-1,c-1);
}
int main()
{ll a,b,c;while(1){cin>>a>>b>>c;if(a==-1&&b==-1&&c==-1)return 0;elseprintf("w(%lld, %lld, %lld) = %lld\n",a,b,c,w(a,b,c));}return 0;
}

 天下第一

这个题目是个什么意思呢？ 在最开始我写这道题的时候看不懂。

就是在我们递归的时候，第一个函数变量放的是(x+y)%mod;  这个就为新的x 那么新的y就是((x+y)%mod+y)%mod 所以是不需要进行分奇偶讨论的，直接这样。

刚刚讲的是这个题目的坑点之一，接下来是第二个坑点：

数据大小，这个的数据大小比较小，而题目卡这个数据很死，所以我们就将最耗空间的二维数组开为short类型。

第三就是error的判断：如果一个数已经出现过了，那么再一次出现就说明进入了死循环，这个时候就分不出胜负了，所以将重复出现的数进行标记，标记为-1，将这个特判条件放在第一位，如果为-1，直接返回-1，再在主函数进行分类讨论

代码如下

#include<iostream>
#include<cstdio>
using namespace std;
int n,mod;short a[10010][10010];
int dfs(int x,int y)
{if(a[x][y]==-1) return -1;if(a[x][y]) return a[x][y];a[x][y]=-1;if(x==0) return a[x][y]=1;if(y==0) return a[x][y]=2;int tmp=(x+y)%mod;return a[x][y]=dfs(tmp,(tmp%mod+y)%mod);
}
int main()
{cin>>n>>mod;int x,y;for(int i=1;i<=n;i++){cin>>x>>y;if(dfs(x,y)==1)printf("%d\n",1);if(dfs(x,y)==2)printf("%d\n",2);if(dfs(x,y)==-1)printf("error\n");}return 0;
}