给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
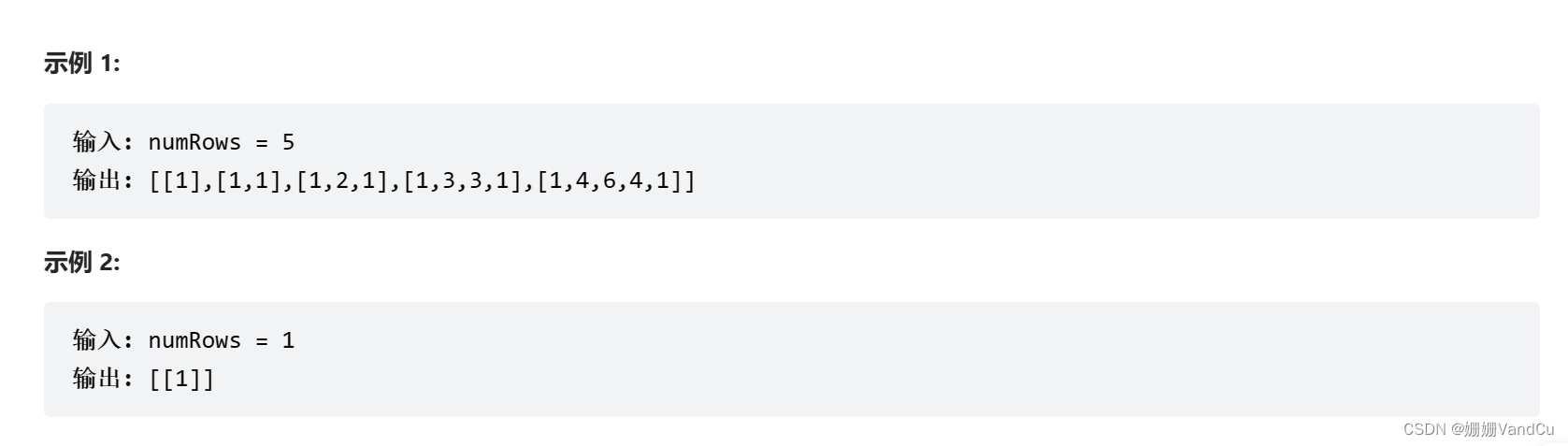
思路:双循环,一个是层数,一个是当前数组的生成;两侧为1,需要边界判断条件;中间生成的公式res[row-1][i-1] + res[row-1][i]为插入数值;
!!!不能直接二位数组插入单个字符元素,可以先生成temp数组,一行结束后讲temp以元素形式插入到res结果数组中。
!!!记得temp清空temp.clear()
#include <iostream>
#include <vector>using namespace std;class Solution {
public:vector<vector<int>> generate(int numRows) {vector<vector<int>> res;vector<int> temp;for (int row = 0; row < numRows; row++){for (int i = 0; i < row + 1; i++){if (i == 0 || i == row){temp.push_back(1);}else{temp.push_back(res[row-1][i-1] + res[row-1][i]);}}res.push_back(temp); // 保存前一行temp.clear(); // 清空临时数组}return res;}
};int main(){Solution s;vector<vector<int>> res = s.generate(5);cout << "[";for (auto i : res){if (i == res[0]) cout << "[";else cout << ",[";for (auto j : i){if (j == i[0]) cout << j;else cout << "," << j;}cout << "]";}cout << "]";return 0;
}
给定一个非负索引 rowIndex,返回「杨辉三角」的第 rowIndex 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。

思路:在原有基础上改进的算法,就是输出最后一行,浪费资源,时间复杂度较高
!!!看了示例代码,才知道杨辉三角可以推导,不得不说,单循环遍历就够了,直接生成
#include <iostream>
#include <vector>using namespace std;// class Solution {
// public:
// vector<int> getRow(int rowIndex) {
// vector<vector<int>> res;
// vector<int> temp;
// for (int row = 0; row <= rowIndex; row++){
// for (int i = 0; i <= row; i++){
// if (i == 0 || i == row){
// temp.push_back(1);
// }
// else{
// temp.push_back(res[row-1][i-1] + res[row-1][i]);
// }
// }
// res.push_back(temp); // 保存前一行
// temp.clear(); // 清空临时数组
// }
// return res[rowIndex];
// }
// };class Solution {
public:vector<int> getRow(int rowIndex) {vector<int> ans = {1};long long c = rowIndex;int n = rowIndex;for (int i = 1; i <= rowIndex;) {ans.push_back(c);c *= --n;c /= ++i;}return ans;}
};
int main(){Solution s;vector<int> res = s.getRow(3);for (int i = 0; i < res.size(); i++){cout << res[i] << " ";}cout << endl;return 0;
}