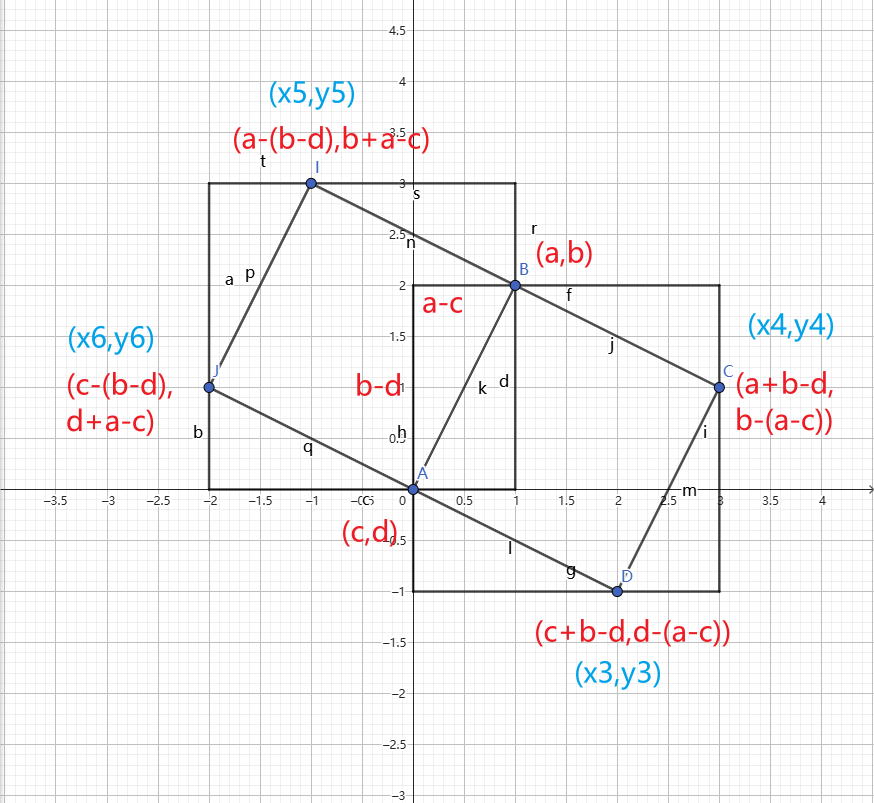
考虑一个答案的超集 \(S = \cup_{i = 1} ^ n [i - a_i + 1, i + a_i - 1]\)。
寻找更多的必要条件,对于 \(1\le x < y\le n\),若 \(\max(a_x, a_y) \le y - x\) 则起点 \(x\sim y\) 无效。
而 \(x + a_x - 1 < y\) 且 \(x < y - a_y + 1\),说明起点 \(1\sim x - 1\) 和 \(y + 1\sim n\) 都无效。
发现两者加起来是充要条件,所以起点集合要么是 \(S\),要么为空。
条件过于复杂,考虑如何转化为简单判定。对于当前区间 \([l, r]\),若左边存在 \(x\) 满足 \(a_x = r - x + 1\) 或右边存在 \(x\) 满足 \(a_x = x - l + 1\) 则必须向对应方向拓展,否则默认向左拓展。
发现这样是对的:若存在一对上述 \((x, y)\),那么无法同时向 \(x, y\) 拓展。而如果必须同时拓展,则一定存在这样一对 \((x, y)\)。
考虑区间 dp,设 \(f_{l, r, 0/1}\) 表示区间 \([l, r]\) 拓展至 \([1, n]\),其中 \(a_{1\dots l - 1}\) 和 \(a_{r + 1\dots n}\) 的取值方案数,且是否限定必须拓展右边。
但是 \(S\subset [l, r]\),可以使用二维差分解决。
- 启示:寻找充要条件,多观察问题模型,观察条件形式。
点击查看代码
#include <bits/stdc++.h>
namespace Initial {#define ll long long#define ull unsigned long long#define fi first#define se second#define mkp make_pair#define pir pair <ll, ll>./#define pb push_back#define i128 __int128using namespace std; ll mod;const ll maxn = 3010, inf = 1e18, iv = mod - mod / 2;ll power(ll a, ll b = mod - 2, ll p = mod) {ll s = 1;while(b) {if(b & 1) s = 1ll * s * a %p;a = 1ll * a * a %p, b >>= 1;} return s;}template <class T>const inline ll pls(const T x, const T y) { return x + y >= mod? x + y - mod : x + y; }template <class T>const inline void add(T &x, const T y) { x = x + y >= mod? x + y - mod : x + y; }template <class T>const inline void chkmax(T &x, const T y) { x = x < y? y : x; }template <class T>const inline void chkmin(T &x, const T y) { x = x > y? y : x; }
} using namespace Initial;namespace Read {char buf[1 << 22], *p1, *p2;// #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, (1 << 22) - 10, stdin), p1 == p2)? EOF : *p1++)template <class T>const inline void rd(T &x) {char ch; bool neg = 0;while(!isdigit(ch = getchar()))if(ch == '-') neg = 1;x = ch - '0';while(isdigit(ch = getchar()))x = (x << 1) + (x << 3) + ch - '0';if(neg) x = -x;}
} using Read::rd;ll t, n, f[maxn][maxn][2], res[maxn][maxn], p[maxn], ans[maxn];void solve() {rd(n), rd(mod); p[0] = 1;for(ll i = 1; i <= n; i++) {p[i] = 1, ans[i] = 0;for(ll j = 1; j <= i; j++)p[i] = p[i] * (n - max(j - 1, i - j)) %mod;}for(ll i = 0; i <= n + 1; i++)for(ll j = 0; j <= n + 1; j++)f[i][j][0] = f[i][j][1] = res[i][j] = 0;f[1][n][0] = 1;for(ll l = 1; l <= n; l++)for(ll r = l > 1? n : n - 1; r >= l; r--) {f[l][r][0] = (f[l - 1][r][0] + f[l - 1][r][1]) * (n - (r - l + 1)) %mod;f[l][r][1] = (f[l][r + 1][0] + f[l][r + 1][1] * (n - (r - l + 1))) %mod;}for(ll l = 1; l <= n; l++)for(ll r = n; r >= l; r--)res[l][r] = (f[l][r][0] + f[l][r][1]) * p[r - l + 1] %mod;for(ll l = n; l; l--)for(ll r = l; r <= n; r++) {res[l][r] = (res[l][r] + mod * 2 - res[l - 1][r]- res[l][r + 1] + res[l - 1][r + 1]) %mod;add(ans[r - l + 1], res[l][r]);}ans[0] = power(n, n);for(ll i = 1; i <= n; i++) add(ans[0], mod - ans[i]);for(ll i = 0; i <= n; i++) printf("%lld ", ans[i]); puts("");
}int main() {rd(t); while(t--) solve();return 0;
}