一、122.买卖股票的最佳时机 II
力扣题目链接

🦄解题思路:
首先需要明确的几个点:
- 当前只能有最大一支股票
- 每一天操作只能3选1:买or卖or休息
此外,对于贪心,总有像下面图示的一种直觉:如果后一天比今天高,则买,否则不买;这是正确的直觉:
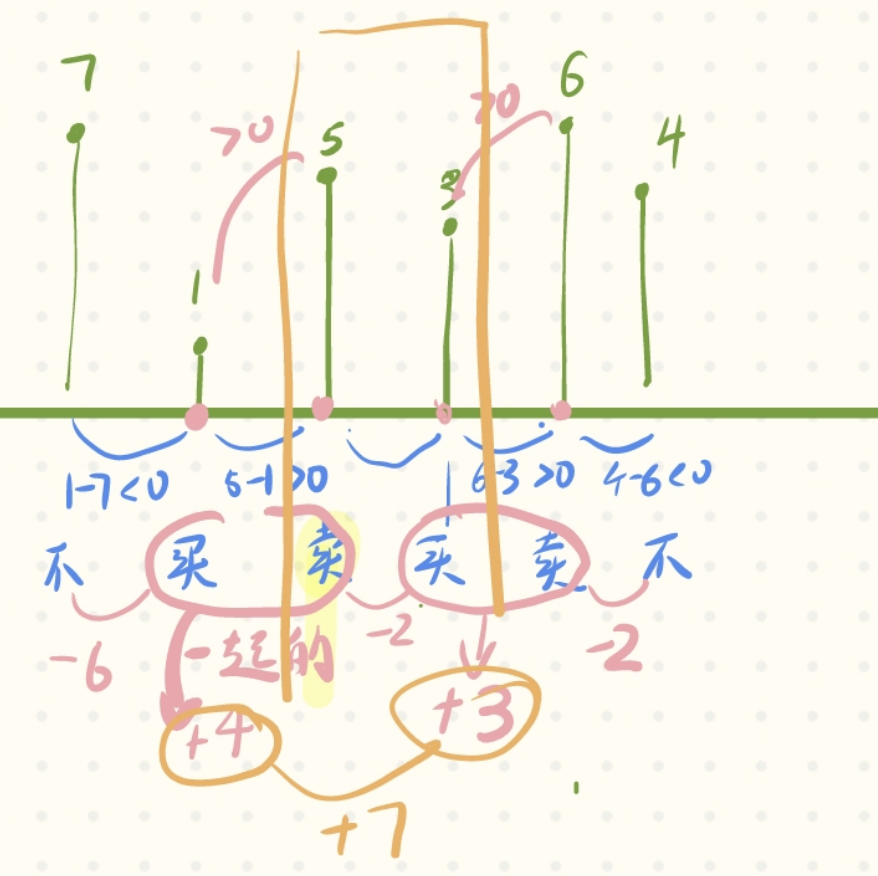
那么这里可能想给出这样的一个思路:
- 若当前元素的价格低于后面元素,则买入,并在后面一个元素卖出:相当于:确定了,今天买,必须明天卖;如此遍历。
- 若当前元素的价格高于后面元素,则当前元素不动,即休息一天。
没错,很有道理,但是我想到了一个反例:
如下图,如果按照上面的思路,则第一个元素买入,第二个元素卖出;遍历到第二个元素时,由于已经卖出,按理来说不能再操作了,但是由于当前元素低于第三个元素,还应该买下第二个元素,这样似乎违法了每天只能有一个操作的前提。
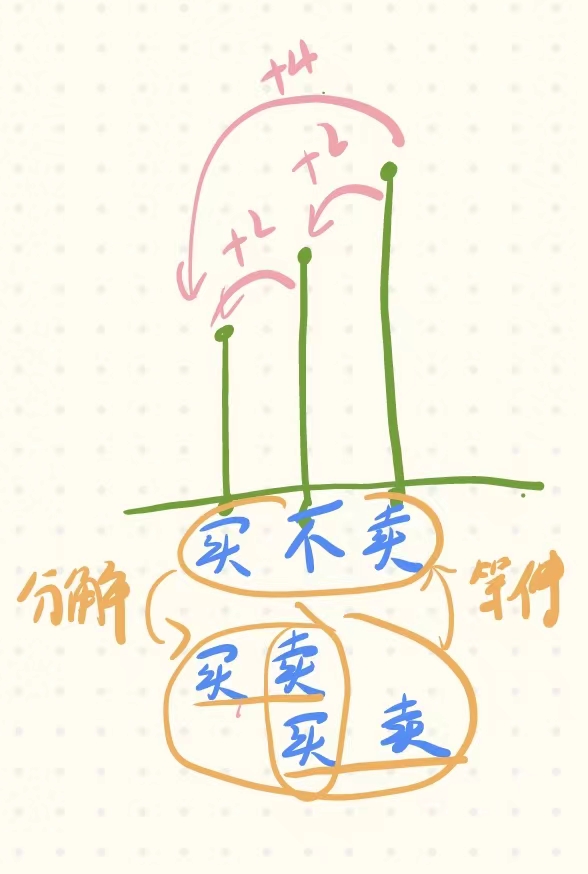
但是后来看了一些题解,发现这种情况根本不影响,虽然正确情况的:第 0 天买入,第 2 天卖出,那么利润为:prices[2] - prices[0]。相当于 (prices[2] - prices[1]) + (prices[1] - prices[0])。也正是由于这种情况,也就是说,计算过程并不等同于实际交易过程,但是计算买卖利润的总和的结果(prices[2] - prices[1]) + (prices[1] - prices[0]),和实际交易情况prices[2] - prices[0]的结果一致,这也是为什么可以这么算!
而且还要发现一点的是,买和卖总是一个单位,它们之间可能有“休息”,像上图一样,但是分解过后,还是两天“买”和“卖”为一个单元。只有这样才能获得最大利润。
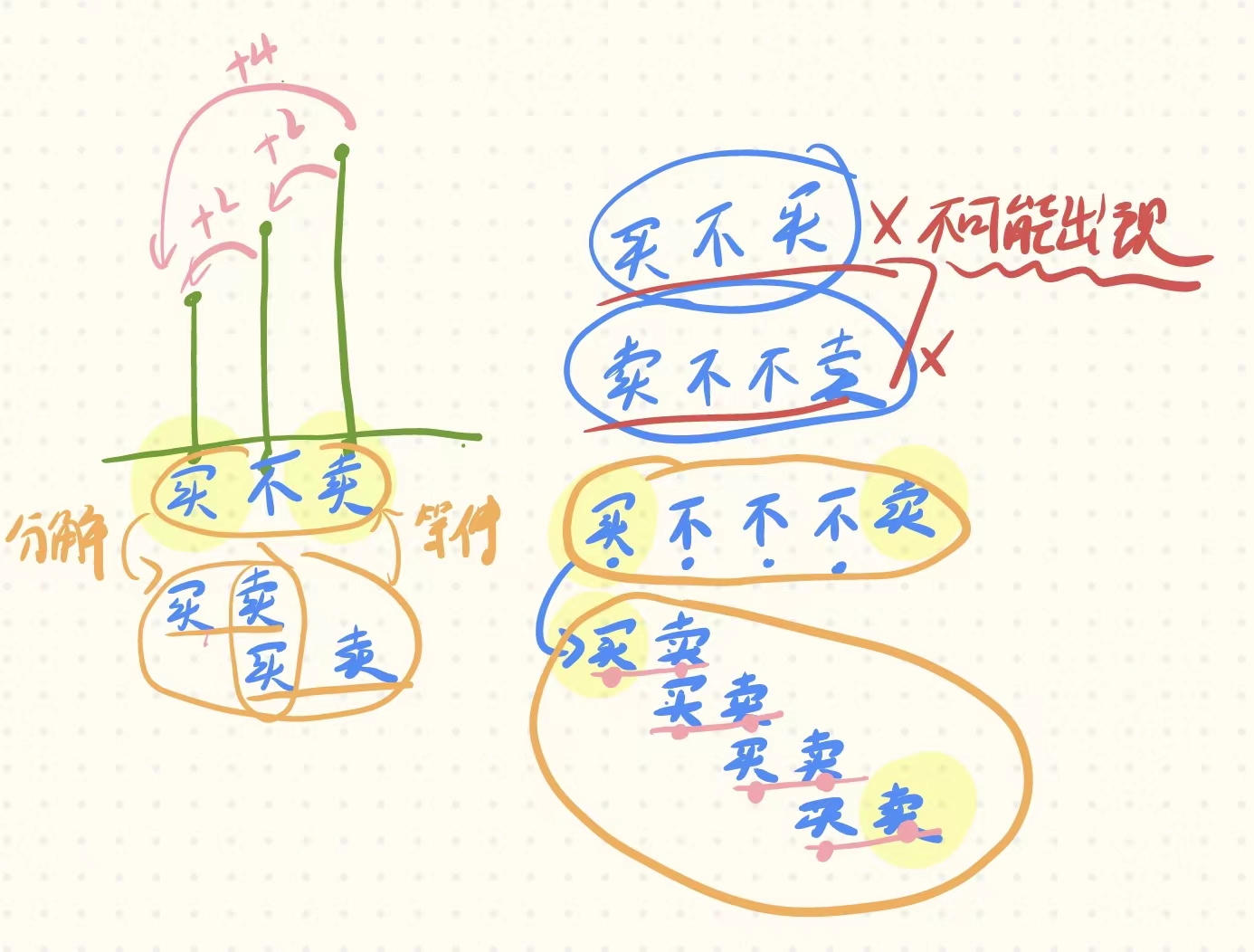
所以这题还是一个比较偏直觉的,一开始可能会像我一样,死磕在当前这一天的操作上(一天操作只能三选一),从而无法下手。
所以具体算法过程如下,贪心贪的就是收集所有正项:
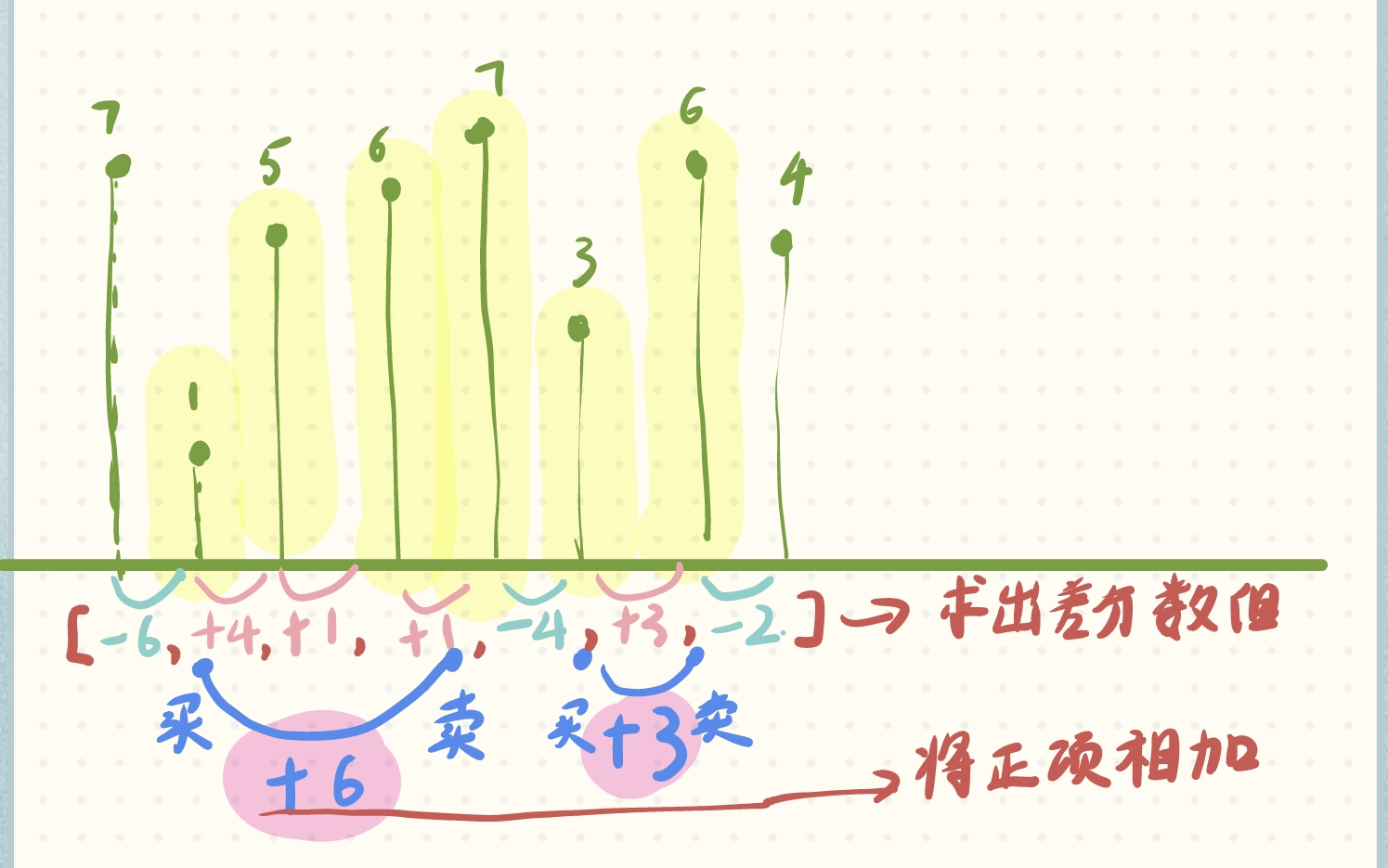
贪心算法和动态规划相比,它既不看前面(也就是说它不需要从前面的状态转移过来),也不看后面(无后效性,后面的选择不会对前面的选择有影响),因此贪心算法时间复杂度一般是线性的,空间复杂度是常数级别的;
✅正确代码:
class Solution {
public:int maxProfit(vector<int>& prices) {int res = 0;for (int i = 1; i < prices.size(); i++){res += max(prices[i]-prices[i-1],0);}return res;}
};
二、55. 跳跃游戏
力扣题目链接

🦄解题思路:
我个人在做这题时并没有做出来,而是陷入了两个思维误区:
- 总是在想,比如当前位于元素值为3的位置,我是走1步还是走2步呢?还是3步呢?
- 好像有点像动态规划的跳楼梯?但是似乎不能从后往前推?状态方程很难确定
其实这题还是贪心,而且它根本不拘泥与到底跳多少步,而是你能跳到哪?或者说你最远能跳到哪里!你跳跃的覆盖范围!为什么这么说呢,可以看下面的图解:
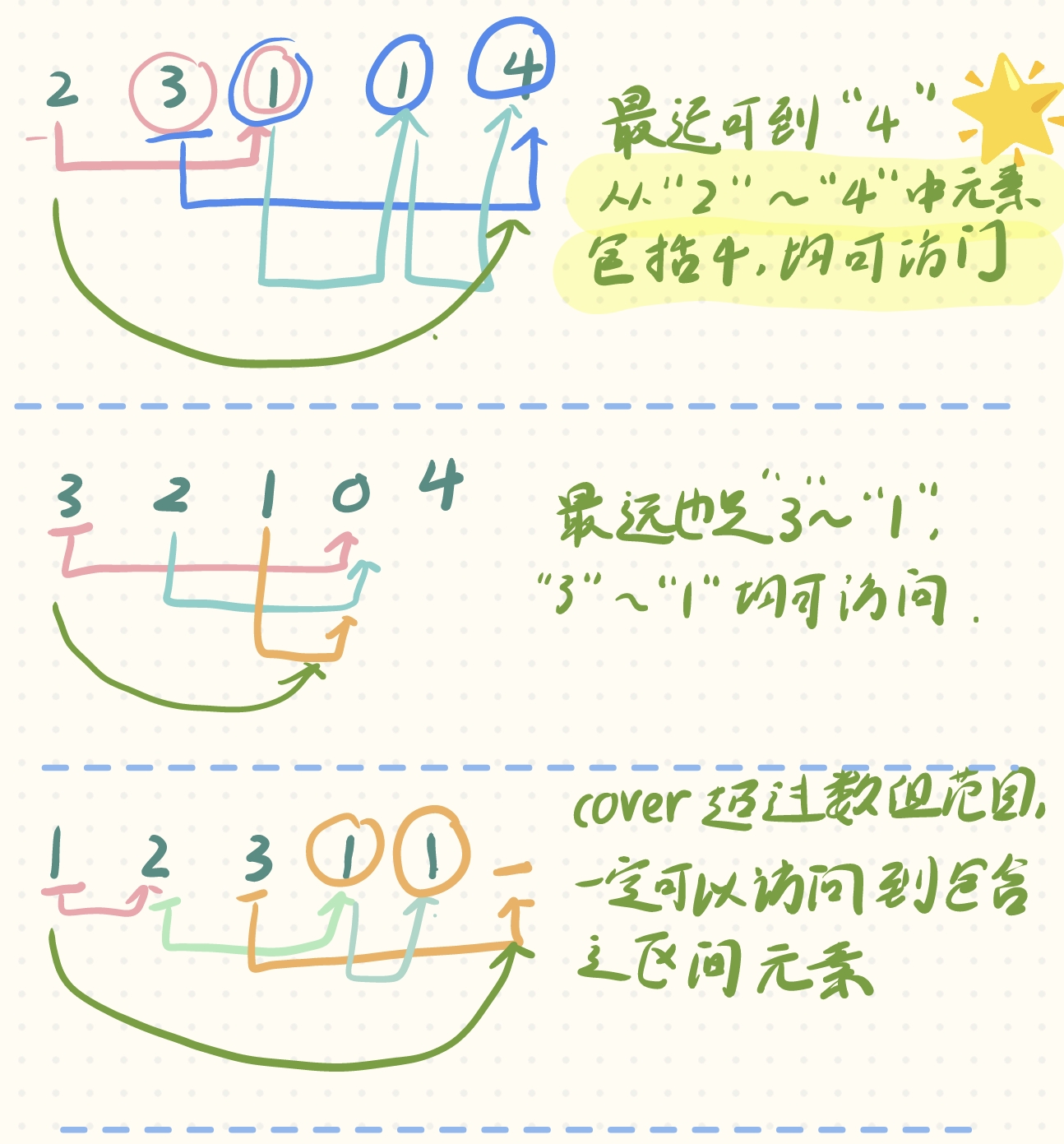
所以这题的coding核心如下
- cover变量,实时记录和更新当前cover的最远距离
- for循环逐个遍历数组元素,更新cover(注意for循环的边界
❌错误代码和分析1:
class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0;//表示当前覆盖长度for (int i = 0; i < nums.size() - 1; i++){cover = max(i+1+nums[i],cover);}return cover >= nums.size()? true : false;}
};
- 没有考虑只有一个元素:

❌错误代码和分析2:
class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0;//表示当前覆盖长度if (nums.size() == 1) return true; // 只有一个元素,就是能达到for (int i = 0; i < nums.size() - 1; i++){cover = max(i+1+nums[i],cover);}return cover >= nums.size()? true : false;}
};
- for循环边界不是
nums.size()-1而是cover!指到这个元素,确定范围cover,起码你要能到这个元素吧。遍历都是要遍历能到达的元素(也就是cover内的,即使cover是随时更新的)。比如这个第一个元素是0,那么你都到不了第二个元素;

✅正确代码:
class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0;//表示当前覆盖数组范围if (nums.size() == 1) return true; // 只有一个元素,就是能达到for (int i = 0; i <= cover; i++){cover = max(i + nums[i],cover);if (cover >= nums.size()-1) return true; // 说明可以覆盖到终点了}return false;}
};