文章目录
- 卷积神经网络
- 卷积
- 转置卷积
- 卷积核和反卷积的三种实现方式
- 卷积的次数计算
卷积神经网络
在神经网络的卷积层中,向下取整(Floor)是一种常用的策略,特别是在处理输出尺寸不是整数的情况时。当你计算出卷积层输出的尺寸(通常是宽度和高度)不是整数时,你可以简单地去掉小数部分,即对该数进行向下取整。
向下取整通常意味着在卷积操作中你可能会忽略输入矩阵(也就是图像或者上一层的输出)的一小部分。这可能导致一些空间信息的丢失,但在实践中通常不会产生重大影响。
举一个简单的例子,假设你有一个7x7的输入和一个3x3的卷积核,步长为2。通常,输出的尺寸会用以下公式来计算:
输出尺寸 = ⌊ 输入尺寸 − 核尺寸 步长 ⌋ + 1 \text{输出尺寸} = \left\lfloor \frac{{\text{输入尺寸} - \text{核尺寸}}}{\text{步长}} \right\rfloor + 1 输出尺寸=⌊步长输入尺寸−核尺寸⌋+1
如果用这个公式计算,输出尺寸会是:
⌊ 7 − 3 2 ⌋ + 1 = 3 \left\lfloor \frac{{7 - 3}}{2} \right\rfloor + 1 = 3 ⌊27−3⌋+1=3
这里,向下取整实际上没有影响,因为计算结果刚好是一个整数。但如果输入尺寸是8x8,那么输出尺寸会是:
⌊ 8 − 3 2 ⌋ + 1 = ⌊ 5 2 ⌋ + 1 = 2 + 1 = 3 \left\lfloor \frac{{8 - 3}}{2} \right\rfloor + 1 = \left\lfloor \frac{5}{2} \right\rfloor + 1 = 2 + 1 = 3 ⌊28−3⌋+1=⌊25⌋+1=2+1=3
在这个例子中,尽管精确的计算结果是3.5,但通过向下取整,输出尺寸变成了3。
使用向下取整的一个优点是它简化了实现,因为你不需要特别处理边界条件。缺点是可能会丢失一些空间信息,尤其是当步长比较大的时候。然而,在许多应用场景中,这种信息丢失通常是可以接受的。
神经网络中关于卷积池化的计算(不为整数时,卷积向下取整,池化向上取整)


对于正向传播,我们使用原始的卷积核进行卷积操作。在反向传播时,为了计算输入或权重的梯度,通常需要进行“翻转”操作。
需要注意的是,正向卷积和反向传播中的卷积(通常称为转置卷积或反卷积)在数学和实现上有一些不同。在正向传播中,卷积核与输入数据进行卷积以生成输出。而在反向传播中,我们关心的是如何改变输入或卷积核以最小化某个损失函数。
为了具体说明为什么需要翻转卷积核,考虑一维情况(二维情况是类似的):
假设正向卷积表示为 y = x ∗ w y = x * w y=x∗w,其中 x x x 是输入, w w w 是卷积核, y y y 是输出,‘*’ 是卷积操作。
在反向传播过程中,我们通常需要计算损失函数 L L L 关于输入 x x x 的梯度( ∂ L ∂ x \frac{\partial L}{\partial x} ∂x∂L)。为了找到这个梯度,我们需要用到链式法则:
∂ L ∂ x = ∂ L ∂ y ∗ rot180 ( w ) \frac{\partial L}{\partial x} = \frac{\partial L}{\partial y} * \text{rot180}(w) ∂x∂L=∂y∂L∗rot180(w)
其中, rot180 ( w ) \text{rot180}(w) rot180(w) 表示将 w w w 进行180度翻转。
这样做的主要原因是数学上的一致性和计算的方便性。这样,前向和反向传播可以用相似的卷积操作来实现,大大简化了算法的实现。
简而言之,在正向传播中我们使用原始的卷积核,而在反向传播时,为了计算梯度,我们通常需要用到翻转的卷积核。这主要是为了数学和计算的方便。
在反向传播(backpropagation)过程中,通常会使用原始卷积核(kernel)的翻转版本。这里的“翻转”通常意味着沿两个空间维度(即不是批量维度或通道维度)旋转180度。
例如,如果你有一个3x3的卷积核:
K = ( a b c d e f g h i ) K = \begin{pmatrix}a & b & c \\d & e & f \\g & h & i\end{pmatrix} K= adgbehcfi
翻转这个卷积核会得到:
K rot = ( i h g f e d c b a ) K^{\text{rot}} = \begin{pmatrix}i & h & g\\f & e & d \\c & b & a\end{pmatrix} Krot= ifchebgda
在Eigen中,使用reverse()函数并指定需要翻转的维度可以实现这一点。例如,对于一个Eigen::MatrixXf对象kernel,你可以这样翻转它:
Eigen::MatrixXf rotated_kernel = kernel.reverse();
这里简单假设reverse()默认沿两个维度翻转矩阵。实际使用中,请确保你正确地翻转了维度。
这个翻转的卷积核(或旋转180度的卷积核)通常用于反向传播过程中,以计算相对于输入的梯度。这与前向传播中使用的卷积核是同一个卷积核,只是翻转了。
【卷积神经网络中的反向传播动画演示】
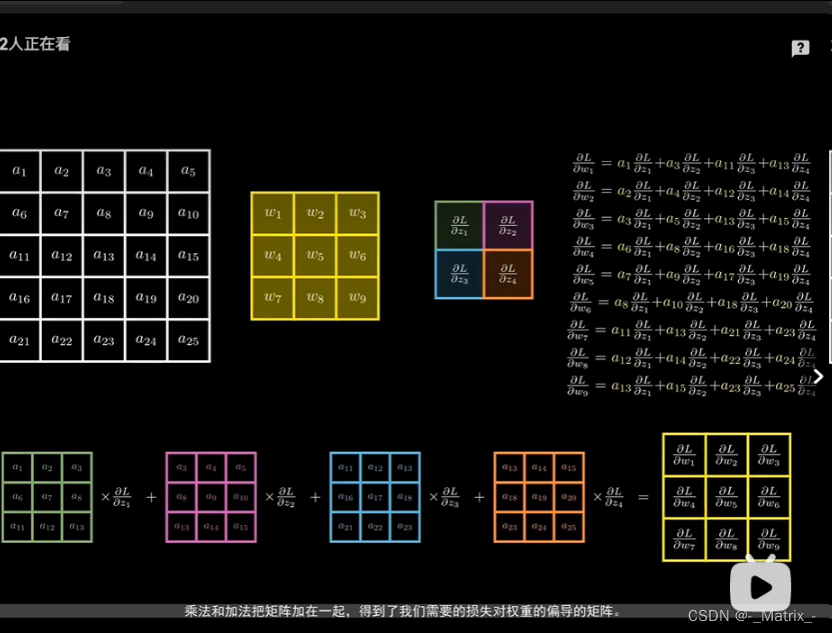
通过将输入和卷积核展开(unroll)为矩阵,可以使用矩阵乘法来实现卷积和转置卷积操作。下面简要介绍如何使用这种技术。
卷积
假设我们有一个输入矩阵 X X X 和一个卷积核 K K K。我们首先将 X X X 展开为一个大矩阵 X unroll X_{\text{unroll}} Xunroll,其中每一列都包含一个 K K K 能应用于 X X X 的局部区域。然后,我们将 K K K 展开为一个行向量 K unroll K_{\text{unroll}} Kunroll。
接下来,卷积操作可以通过以下矩阵乘法进行:
O = K unroll × X unroll O = K_{\text{unroll}} \times X_{\text{unroll}} O=Kunroll×Xunroll
其中 O O O 是输出矩阵。
转置卷积
对于转置卷积,方法基本相同,但展开和乘法的方向会有所不同。
假设我们有一个输入矩阵 Y Y Y 和相同的卷积核 K K K。为了进行转置卷积,我们将 Y Y Y 展开为 Y unroll Y_{\text{unroll}} Yunroll,然后执行以下矩阵乘法:
O = X unroll × K T O = X_{\text{unroll}} \times K^T O=Xunroll×KT
这里, K T K^T KT 是 K K K 的转置。
请注意,在这两种情况下,我们都需要格外注意矩阵的维度和展开的顺序。
卷积核和反卷积的三种实现方式
#include <Eigen/Dense>
#include <iostream>//卷积
Eigen::MatrixXf conv2D(const Eigen::MatrixXf& input, const Eigen::MatrixXf& kernel, int stride) {// 计算输出矩阵的尺寸int rows = (input.rows() - kernel.rows()) / stride + 1;int cols = (input.cols() - kernel.cols()) / stride + 1;// 创建输出矩阵Eigen::MatrixXf output(rows, cols);for (int i = 0; i < rows; ++i) {for (int j = 0; j < cols; ++j) {// 计算每个输出元素Eigen::MatrixXf block = input.block(i * stride, j * stride, kernel.rows(), kernel.cols());output(i, j) = (block.array() * kernel.array()).sum();}}return output;
}// deconv2D 是一个函数,用于执行反卷积(也叫转置卷积)
Eigen::MatrixXf deconv2D( const Eigen::MatrixXf& y_grad,const Eigen::MatrixXf& kernel, int stride) {// 计算输出尺寸int outputRows = (y_grad.rows() - 1) * stride + kernel.rows();int outputCols = (y_grad.cols() - 1) * stride + kernel.cols();// 初始化输出矩阵为零Eigen::MatrixXf output = Eigen::MatrixXf::Zero(outputRows, outputCols);// 进行转置卷积操作for (int i = 0; i < y_grad.rows(); ++i) {for (int j = 0; j < y_grad.cols(); ++j) {// 注意:这里我们假设步长(stride)是1,你可以通过修改下面的索引来调整步长output.block(i * stride, j * stride, kernel.rows(), kernel.cols()) += y_grad(i, j) * kernel;}}return output;
}// 转置卷积
Eigen::MatrixXf Conv2DTransposed( int rows,int cols ,const Eigen::MatrixXf& kernel, int stride)
{int r = (rows - kernel.rows()) / stride + 1;int c = (cols - kernel.cols()) / stride + 1;// 初始化输出矩阵为零Eigen::MatrixXf output1 = Eigen::MatrixXf::Zero(r * c, rows * cols);int jj =0;// 进行转置卷积操作for (int i = 0; i < r; ++i){for (int j = 0; j < c ; ++j){// 初始化输出矩阵为零Eigen::MatrixXf output = Eigen::MatrixXf::Zero(rows, cols);// 注意:这里我们假设步长(stride)是1,你可以通过修改下面的索引来调整步长output.block(i * stride, j * stride, kernel.rows(), kernel.cols()) = kernel;output1.row(jj++) = output.reshaped<Eigen::RowMajor>();}}return output1;
}
//图像转换为列
Eigen::MatrixXf im2col(const Eigen::MatrixXf& input, int kernel_rows, int kernel_cols, int stride) {int output_rows = (input.rows() - kernel_rows) / stride + 1;int output_cols = (input.cols() - kernel_cols) / stride + 1;Eigen::MatrixXf output(kernel_rows * kernel_cols, output_rows * output_cols);int col_idx = 0;for (int row = 0; row <= input.rows() - kernel_rows; row += stride){for (int col = 0; col <= input.cols() - kernel_cols; col += stride){Eigen::VectorXf col_vector = input.block(row, col, kernel_rows, kernel_cols).reshaped<Eigen::RowMajor>();//const Eigen::VectorXf col_vector = Eigen::Map<const Eigen::VectorXf, Eigen::RowMajor>(block.data(), block.size());output.col(col_idx++) = col_vector;}}return output;
}//列转换为图像
Eigen::MatrixXf col2im(const Eigen::MatrixXf& input, int original_rows, int original_cols, int kernel_rows, int kernel_cols, int stride) {Eigen::MatrixXf output = Eigen::MatrixXf::Zero(original_rows, original_cols);int col_idx = 0;for (int row = 0; row <= original_rows - kernel_rows; row += stride){for (int col = 0; col <= original_cols - kernel_cols; col += stride){Eigen::MatrixXf block = input.col(col_idx++).reshaped<Eigen::RowMajor>(kernel_rows, kernel_cols);//const Eigen::MatrixXf block = Eigen::Map<const Eigen::MatrixXf, Eigen::RowMajor>(col_vector.data(), kernel_rows, kernel_cols);output.block(row, col, kernel_rows, kernel_cols) += block;}}return output;
}int main() {// 用于测试的输入和卷积核Eigen::MatrixXf input(5, 5);input << 1, 2, 3, 4, 5,5, 4, 3, 2, 1,1, 2, 3, 4, 5,5, 4, 3, 2, 1,1, 2, 3, 4, 5;Eigen::MatrixXf kernel(3, 3);kernel << 1, 0, -1,1, 5, -1,1, 4, -1;int stride = 2;//第一种实现:正常卷积{//卷积Eigen::MatrixXf output = conv2D(input, kernel, stride);std::cout << "1: Conv2D Output:\n" << output << std::endl;//反卷积Eigen::MatrixXf output1 = deconv2D(output,kernel, stride);std::cout << "1: deconv2D output1:\n" << output1 << std::endl;}//第二种实现:转置卷积{Eigen::MatrixXf Unfold = Conv2DTransposed(input.rows(),input.cols(),kernel,stride);std::cout << "2: Unfold:\n" << Unfold << std::endl;Eigen::VectorXf Input = input.reshaped<Eigen::RowMajor>();Eigen::MatrixXf output = Unfold * Input;std::cout << "2: Conv2D Output:\n" << output << std::endl;Eigen::MatrixXf output1 = (Unfold.transpose() * output).reshaped<Eigen::RowMajor>(input.rows(),input.cols());std::cout << "2: deconv2D output1:\n" << output1 << std::endl;}//第三种种实现:图像转换为列 矩阵相乘实现 加速运算{Eigen::MatrixXf input_unroll = im2col(input, kernel.rows(),kernel.cols(), stride);Eigen::RowVectorXf kernel_unroll = kernel.reshaped<Eigen::RowMajor>();Eigen::MatrixXf output = kernel_unroll * input_unroll ;std::cout << "3: Conv2D Output:\n" << output << std::endl;Eigen::MatrixXf output_unroll11 = kernel_unroll.transpose() * output;std::cout << "3: output_unroll11:\n" << output_unroll11 << std::endl;Eigen::MatrixXf output1 = col2im(output_unroll11, input.rows(),input.cols(),kernel.rows(),kernel.cols(), stride);std::cout << "3: deconv2D output1:\n" << output1 << std::endl;}}
1: Conv2D Output:
26 24
26 24
1: deconv2D output1:26 0 -2 0 -2426 130 -2 120 -2452 104 -4 96 -4826 130 -2 120 -2426 104 -2 96 -24
2: Unfold:1 0 -1 0 0 1 5 -1 0 0 1 4 -1 0 0 0 0 0 0 0 0 0 0 0 00 0 1 0 -1 0 0 1 5 -1 0 0 1 4 -1 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 1 0 -1 0 0 1 5 -1 0 0 1 4 -1 0 00 0 0 0 0 0 0 0 0 0 0 0 1 0 -1 0 0 1 5 -1 0 0 1 4 -1
2: Conv2D Output:
26
24
26
24
2: deconv2D output1:26 0 -2 0 -2426 130 -2 120 -2452 104 -4 96 -4826 130 -2 120 -2426 104 -2 96 -24
3: Conv2D Output:
26 24 26 24
3: output_unroll11:26 24 26 240 0 0 0
-26 -24 -26 -2426 24 26 24
130 120 130 120
-26 -24 -26 -2426 24 26 24
104 96 104 96
-26 -24 -26 -24
3: deconv2D output1:26 0 -2 0 -2426 130 -2 120 -2452 104 -4 96 -4826 130 -2 120 -2426 104 -2 96 -24
卷积的次数计算

当然可以。给定一个输入特征图的大小和一个滤波器的大小,以及卷积的步长和填充,以下是如何计算卷积后的输出特征图的维度的完整公式:
-
高度 H 2 H_2 H2 的计算:
H 2 = H 1 − F H + 2 P S + 1 H_2 = \frac{H_1 - F_{H} + 2P}{S} + 1 H2=SH1−FH+2P+1 -
宽度 W 2 W_2 W2 的计算:
W 2 = W 1 − F W + 2 P S + 1 W_2 = \frac{W_1 - F_{W} + 2P}{S} + 1 W2=SW1−FW+2P+1
其中:
- H 1 , W 1 H_1, W_1 H1,W1 是输入特征图的高和宽。
- F H , F W F_H, F_W FH,FW 是滤波器的高和宽。
- P P P 是填充的数量。
- S S S 是步长。
以下是使用C++和Eigen库实现的示例:
#include <Eigen/Dense>
#include <iostream>
#include <cmath>std::pair<int, int> computeConvTimes(int input_rows, int input_cols, int kernel_rows, int kernel_cols, int stride) {int rows_times = (input_rows - kernel_rows) / stride + 1;int cols_times = (input_cols - kernel_cols) / stride + 1;return {rows_times, cols_times};
}int main() {int input_rows = 5, input_cols = 5;int kernel_rows = 3, kernel_cols = 3;int stride = 2;auto [rows_times, cols_times] = computeConvTimes(input_rows, input_cols, kernel_rows, kernel_cols, stride);std::cout << "Rows can be convolved: " << rows_times << " times.\n";std::cout << "Columns can be convolved: " << cols_times << " times.\n";return 0;
}
这段代码首先定义了一个函数computeConvTimes,该函数使用上述公式计算行和列的卷积次数。然后在main函数中展示了对于给定的输入大小、核大小和步长,可以进行多少次卷积操作。