动态规划课堂2-----路径问题

目录

引言：

例题1：不同路径

例题2：不同路径II

例题3：礼物的最⼤价值

例题4：下降路径最⼩和

例题5：最小路径和

结语：

引言：

在学习完动态规划斐波那契数列模型后，相信大家对动态规划已经有了一定的了解，下面我们继续深入学习动态规划的路径问题，我们一般的解题步骤还是1. 状态表示，2.状态转移方程，3.初始化，4.填表顺序，5.返回值。在写代码时一定要把这5步考虑清楚再写代码，写代码的步骤为1.创建 dp表2.初始化3.填表4.返回值。

例题1：不同路径

链接：不同路径

题目简介：

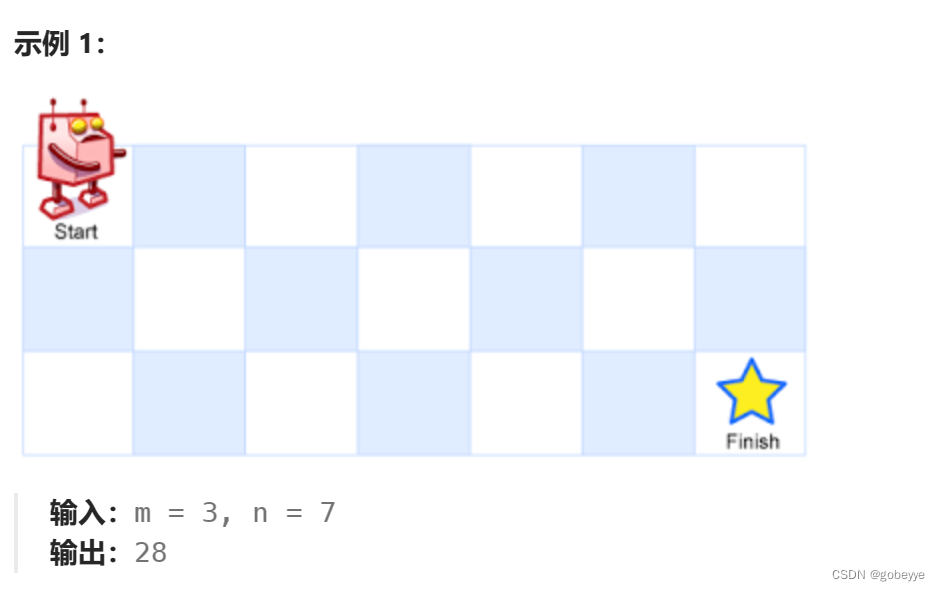
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

解法（动态规划）：

1. 状态表示：

对于这种「路径类」的问题，我们的状态表⽰⼀般有两种形式：

（1）从[i, j] 位置出发到终点有几种路径。

（2）从起始位置出发，到达[i, j] 位置有几种路径。

本题我们选择第二种，dp[i][j] 表示：⾛到[i, j] 位置处，⼀共有多少种⽅式。

2.状态转移方程

简单分析⼀下。如果dp[i][j] 表⽰到达[i, j] 位置的⽅法数，那么到达[i, j] 位置之 前的⼀⼩步，有两种情况：

（1）从[i, j] 位置的上⽅（ [i - 1, j] 的位置）向下⾛⼀步，转移到[i, j] 位置

（2）从[i, j] 位置的左⽅（ [i, j - 1] 的位置）向右⾛⼀步，转移到[i, j] 位置。

由于我们要求的是有多少种⽅法，因此状态转移⽅程就呼之欲出了： dp[i][j] = dp[i - 1] [j] + dp[i][j - 1] 。

3.初始化

使用辅助结点 。

注意点：（1）辅助结点⾥⾯的值要「保证后续填表是正确的」（2）下标的映射关系。在本题中，「添加⼀⾏」，并且「添加⼀列」后，只需将dp[0][1] 的位置初始化为1 即可。

4.填表顺序

根据「状态转移⽅程」的推导来看，填表的顺序就是「从上往下」填每⼀⾏，在填写每⼀⾏的时候 「从左往右」。

5.返回值

根据「状态表⽰」，我们要返回dp[m][n]（添加了一个辅助节点） 的值 。

代码如下：

动态规划编写代码的步骤比较固定，上面那5步是想好思路，下面这4步是编写代码的步骤。

class Solution {public int uniquePaths(int m, int n) {//1.创建dp表//2.初始化//3.填表//4.返回值int[][] dp = new int[m + 1][n + 1];dp[0][1] = 1;for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}
}

时间复杂度：O（n * m）

空间复杂度：O（n * m）

例题2：不同路径II

链接：不同路径II

题目简介：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

 解法（动态规划）：

本题是例题一的进阶版，但是两题的解题步骤是类似的不同的地方在于状态转移方程。[i - 1, j] 与[i, j - 1] 位置都是可能有障碍的，此时从上⾯或者左边是不可能到达[i, j] 位置的，也就是说，此时的⽅法数应该是0。由此我们可以得出⼀个结论，只要这个位置上「有障碍物」，那么我们就不需要计算这个位置上的值，直接让它等于0即可。

代码如下：

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {//1.创建dp表//2.初始化//3.填表//4.返回值int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] dp = new int[m + 1][n + 1];dp[0][1] = 1;for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){if(obstacleGrid[i - 1][j - 1] == 1){dp[i][j] = 0;}else{dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}}return dp[m][n];}
}

时间复杂度：O（n * m）

空间复杂度：O（n * m）

例题3：礼物的最⼤价值

链接：礼物的最⼤价值

题目简介：

现有一个记作二维矩阵 frame 的珠宝架，其中 frame[i][j] 为该位置珠宝的价值。拿取珠宝的规则为：

  • 只能从架子的左上角开始拿珠宝
  • 每次可以移动到右侧或下侧的相邻位置
  • 到达珠宝架子的右下角时，停止拿取

注意：珠宝的价值都是大于 0 的。除非这个架子上没有任何珠宝，比如 frame = [[0]]。

解法（动态规划）：

1. 状态表示：

dp[i][j] 表⽰：⾛到[i, j] 位置处，此时的最⼤价值。

2.状态转移方程

对于dp[i][j] ，我们发现想要到达[i, j] 位置，有两种⽅式：

(1)从[i, j] 位置的上⽅[i - 1, j] 位置，向下⾛⼀步，此时到达[i, j] 位置能 拿到的礼物价值为dp[i - 1][j] + grid[i][j] .

(2)从[i, j] 位置的左边[i, j - 1] 位置，向右⾛⼀步，此时到达[i, j] 位置能 拿到的礼物价值为dp[i][j - 1] + grid[i][j].

最终dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i][j] 。

3.初始化

添加辅助节点

4.填表顺序

填表的顺序是「从上往下填写每⼀⾏」，「每⼀⾏从左往右」。

5.返回值

返回dp[m][n]的值

代码如下：

class Solution {public int jewelleryValue(int[][] frame) {//1.创建dp表//2.初始化//3.填表//4.返回值int m = frame.length;int n = frame[0].length;int[][] dp = new int[m + 1][n + 1];for(int i = 1;i <= m;i++){for(int j = 1;j <=n;j++){dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]) + frame[i - 1][j - 1];}}return dp[m][n];}
}

时间复杂度：O（n * m）

空间复杂度：O（n * m）

例题4：下降路径最⼩和

链接：下降路径最⼩和

题目简介：

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

解法（动态规划）：

1. 状态表示：

dp[i][j] 表⽰：到达[i, j] 位置时，所有下降路径中的最⼩和。

2.状态转移方程

对于普遍位置[i, j] ，根据题意得，到达[i, j] 位置可能有三种情况：

（1）从正上⽅[i - 1, j] 位置转移到[i, j] 位置.

（2）从左上⽅[i - 1, j - 1] 位置转移到[i, j] 位置；

  (3)   从右上⽅[i - 1, j + 1] 位置转移到[i, j] 位置；

由于我们要的是最小的于是 dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i][j] 。

3.初始化

辅助节点

在本题中，需要「加上⼀⾏」，并且「加上两列」。所有的位置都初始化为⽆穷⼤，然后将第⼀⾏ 初始化为0即可。

4.填表顺序

表的顺序是从上往下。

5.返回值

返回dp表中最后⼀⾏的最⼩值。

代码如下：

class Solution {public int minFallingPathSum(int[][] matrix) {//1.创建dp表//2.初始化//3.填表//4.返回值int m = matrix.length;//yint n = matrix[0].length;//xint[][] dp = new int[m + 1][n + 2];//辅助节点for(int i = 0;i <= m;i++){dp[i][0] = Integer.MAX_VALUE;dp[i][n + 1] = Integer.MAX_VALUE;}for(int i = 1;i <= n;i++){dp[m][i] = Integer.MAX_VALUE;}for(int i = m - 1;i >= 0;i--){for(int j = 1;j <= n;j++){int min = Math.min(Math.min(dp[i + 1][j - 1],dp[i + 1][j]),dp[i + 1][j + 1]);if(min == Integer.MAX_VALUE){min = 0;}dp[i][j] = matrix[i][j - 1] + min;}}int key = dp[0][1];for(int i = 1;i <= n;i++){if(key > dp[0][i]){key = dp[0][i];}}return key;}
}

时间复杂度：O（n * m）

空间复杂度：O（n * m）

例题5：最小路径和

链接：最⼩路径和

题目简介：

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

解法（动态规划）：

1. 状态表示：

dp[i][j] 表⽰：到达[i, j] 位置处，最⼩路径和是多少。

2.状态转移方程

简单分析⼀下。如果dp[i][j] 表⽰到达到达[i, j] 位置处的最⼩路径和，那么到达 [i, j] 位置之前的⼀⼩步，有两种情况：

（1）从[i - 1, j] 向下⾛⼀步，转移到[i, j] 位置；

（2）从[i, j - 1] 向右⾛⼀步，转移到[i, j] 位置。

由于到[i, j] 位置两种情况，并且我们要找的是最⼩路径，因此只需要这两种情况下的最⼩值，再加上 [i, j] 位置上本⾝的值即可。故最终结果为：dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]。

3.初始化

辅助节点

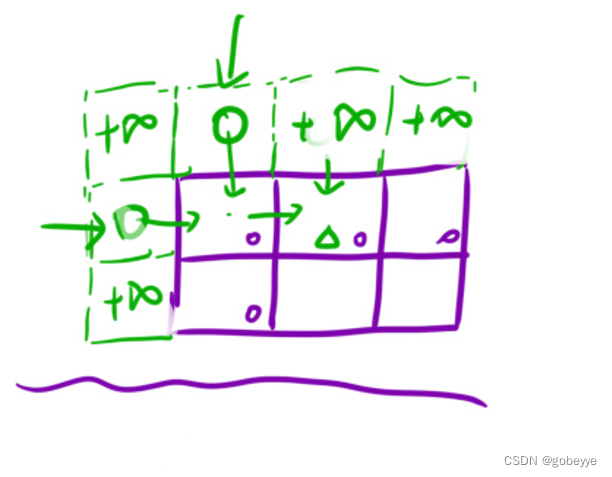
在本题中，「添加⼀⾏」，并且「添加⼀列」后，所有位置的值可以初始化为⽆穷⼤，然后让 dp[0][1] = dp[1][0] = 0 即可。如下图所示：

4.填表顺序

「从上往下」填每⼀⾏，每⼀⾏「从左往右」。

5.返回值

返回的结果是dp[m][n] 。

代码如下：

class Solution {public int minPathSum(int[][] grid) {//1.创建dp表//2.初始化//3.填表//4.返回值int m = grid.length;//yint n = grid[0].length;//xint[][] dp = new int[m + 1][n + 1];for(int i = 2;i <= n;i++){dp[0][i] = Integer.MAX_VALUE;}for(int i = 2;i <= m;i++){dp[i][0] = Integer.MAX_VALUE;}for(int i = 1;i <= m;i++){for(int j = 1;j <= n;j++){dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[m][n];}
}

时间复杂度：O（n * m）

空间复杂度：O（n * m）

结语：

其实写博客不仅仅是为了教大家，同时这也有利于我巩固自己的知识点，和一个学习的总结，由于作者水平有限，对文章有任何问题的还请指出，接受大家的批评，让我改进，如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注，这可以激励我写出更加优秀的文章。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/504450.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

每周一算法：双向广搜

每周一算法：双向广搜

题目链接 字符串变换 题目描述 已知有两个字串 A , B A,B A,B&#xff0c;及一组字串变换的规则&#xff08;至多 6 6 6个规则&#xff09;: A 1 → B 1 A_1→B_1 A1​→B1​ A 2 → B 2 A_2→B_2 A2​→B2​ … 规则的含义为&#xff1a;在 A A A中的子串 A 1 A_1 A1​…
阅读更多...
Java构造方法总结（很清晰）

Java构造方法总结（很清晰）

构造方法扫盲&#xff1a;构造方法就是为了创建对象的 解释&#xff1a;真正创建对象的是 new 这个关键字&#xff0c;Java 虚拟机在创建对象时是有很多步骤的&#xff0c;构造方法只是其中的一步&#xff0c;它的作用是进行成员变量初始化。
阅读更多...
自媒体ChatGPT4.0批量洗稿改写文章软件多开教程

自媒体ChatGPT4.0批量洗稿改写文章软件多开教程

大家好&#xff0c;我是淘小白~ 之前写的软件&#xff0c;ChatGPT4.0洗稿软件&#xff0c;因为是驱动浏览器改写的&#xff0c;还需要过openai官网的机器验证&#xff0c;所以&#xff0c;软件是免登录的&#xff0c;需要我们提前登录好自己的账号信息&#xff0c;软件根据浏览…
阅读更多...
【数据结构】之优先级队列(堆)

【数据结构】之优先级队列(堆)

文章目录 一、优先级队列的概念二、优先级队列的模拟实现1.堆的存储2.堆的创建3.代码的实现 一、优先级队列的概念 队列是一种先进先出(FIFO)的数据结构&#xff0c;但有些情况下&#xff0c;操作的数据可能带有优先级&#xff0c;一般出队列时&#xff0c;可能需要优先级高的…
阅读更多...
2024理解这几个安全漏洞，你也能做安全测试！

2024理解这几个安全漏洞，你也能做安全测试！

如今安全问题显得越来越重要&#xff0c;一个大型的互联网站点&#xff0c;你如果每天查看日志&#xff0c;会发现有很多尝试攻击性的脚本。 如果没有&#xff0c;证明网站影响力还不够大。信息一体化的背后深藏着各类安全隐患&#xff0c;例如由于开发人员的不严谨导致为Web应…
阅读更多...
Java虚拟机（JVM）从入门到实战【上】

Java虚拟机（JVM）从入门到实战【上】

Java虚拟机&#xff08;JVM&#xff09;从入门到实战【上】&#xff0c;涵盖类加载&#xff0c;双亲委派机制&#xff0c;垃圾回收器及算法等知识点&#xff0c;全系列6万字。 一、基础篇 P1 Java虚拟机导学课程 P2 初识JVM 什么是JVM Java Virtual Machine 是Java虚拟机。…
阅读更多...
频率域采样

频率域采样

1. 频率域采样 (1) 采样的过程&#xff1a;DFT的X(k)是对周期且连续的频谱X()在[0,2pi)上的等间隔采样&#xff0c;采N个点得到的&#xff0c;采样间隔是&#xff1b;频域采样要求时域有限&#xff0c;即假设x(n)的长度是有限值M&#xff0c;x(n)的SFT是X()。 (2) X(k) 做IDF…
阅读更多...
live555源码学习（1）

live555源码学习（1）

1 基础组件 live项目主要包含了四个基础库、程序入口类&#xff08;mediaServer&#xff09;和测试程序&#xff08;testProgs&#xff09;。四个基础库是UsageEnvironment、BasicUsageEnvironment、groupsock和liveMedia UsageEnvironment 抽象了两个类UsageEnvironment和T…
阅读更多...
蓝桥杯备战刷题two（自用）

蓝桥杯备战刷题two（自用）

1.杨辉三角形 #include<iostream> using namespace std; #define ll long long const int N2e510; int a[N]; //1 0 0 0 0 0 0 //1 1 0 0 0 0 0 //1 2 1 0 0 0 0 //1 3 3 1 0 0 0 //1 4 6 4 1 0 0 //1 5 10 10 5 1 //前缀和思想 //第一列全为1,第二列为从0开始递增1的序…
阅读更多...
整数和浮点数在内存中的存储（大小端字节序，浮点数的存取）

整数和浮点数在内存中的存储（大小端字节序，浮点数的存取）

目录 1.整数在内存中的存储 2.大小端字节序和字节序判断 2.1什么是大小端&#xff1f; 2.2为什么会有大小端 3.浮点数在内存中的存储 3.1浮点数的存储 3.1.1 浮点数存的过程 3.1.2 浮点数取的过程 3.2 解析 3.3 验证浮点数的存储方式 1.整数在内存中的存储 整数的二进…
阅读更多...
前端工程化(黑马学习笔记)

前端工程化(黑马学习笔记)

前端工程化介绍 我们目前的前端开发中&#xff0c;当我们需要使用一些资源时&#xff0c;例如&#xff1a;vue.js&#xff0c;和axios.js文件&#xff0c;都是直接再工程中导入的&#xff0c;如下图所示&#xff1a; 但是上述开发模式存在如下问题&#xff1a; ● 每次开发都是…
阅读更多...
程序项目打包发布方法，采用InstallShield软件

程序项目打包发布方法，采用InstallShield软件

重点&#xff1a; 1.程序项目做出来了&#xff0c;需要打包发布给用户。如何打包是关键。 2.采用InstallShield软件进行发布。 步骤一&#xff1a;创建一个依赖三方库配置环境的bat文件的项目。 &#xff08;主要测试三方库打包 和如果有bat文件&#xff0c;需要先创建环境&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023