线段树的应用范围非常广，可以处理很多与区间有关的题目。

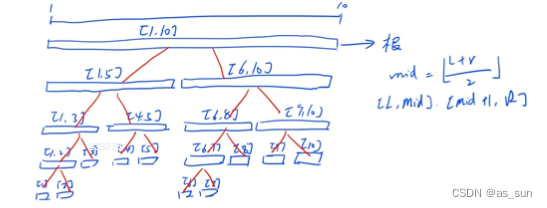
将区间抽象成一个节点，在这个节点中储存这个区间的一些值，那么如果看成节点的话，这就很像一棵满二叉树，所以我们可以用一维数组来储存节点。那么就要考虑父子节点之间的关系。

如果一个一个节点的下标是x，

那么父节点就是x/2

左子节点就是2x(可以写为x<<1),右子节点就是2x+1(可以写为x<<1+1)

那么我们就可以实现节点之间的转移操作，实际上相互影响的也只有父子节点之间相互影响，所以在更新的时候有两种更新方式，一种是用子节点来更新父节点(pushup)，一种是用父节点来更新子节点(pushdown)。

还有一个问题就是这个一维数组该开多大，假设区间大小为n，那么我们就将数组开到4n大小。

既然用线段树，那么肯定要定义结构体来表示每个点，结构体的定义首先要有l,r来表示区间范围，然后需要维护的值肯定要放入结构体中，至于其他的变量就要根据维护值是否能用子节点算出父节点来决定，如果不能的话，那么就要考虑引入新的变量。

线段树看起来似乎很高深，但是实际上只有几个函数，模板比较固定：

build()//初始化线段树

modify()//修改

pushup()//用子节点更新父节点

pushdown()//将父节点的更新传到子节点

query() //查询操作

对于这些操作，我们还是结合具体的例题来分析。

1275. 最大数（活动 - AcWing）

题目稍微翻译一下就是，向一个空数组中插入数，在插入的同时进行局部区间最大值的访问。用上线段树后思路也没什么复杂的，我们可以先将整个数组先用线段树维护起来，空位置对应的区间就是0，那么我向末尾插入数的时候，实际上也就相当于对区间进行单点修改，单点修改的话实际上容易想到树状数组，但是树状数组用到了前缀和的原理，前缀和是没办法解决最大值问题的，所以这里还是要用线段树来实现。

我们先来确定结构体如何确定，首先得有l,r来表示区间，然后max也必须定义在结构体中，然后判断是否能用子节点的值来更新父节点，显然是可以的，父区间的最大值=max(左子区间的最大值，右子区间的最大值)。

#include<bits/stdc++.h>
using namespace std;
const int N=200010;
struct node
{int l,r,mx;
}tr[4*N];
int m,p;
void build(int u,int l,int r)
{tr[u]={l,r};if(l==r) return;int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);}
void pushup(int u)
{tr[u].mx=max(tr[u<<1].mx,tr[u<<1|1].mx);
}
void modify(int u,int x,int c)
{if(tr[u].l==x&&tr[u].r==x) tr[u].mx=c;else{int mid=tr[u].l+tr[u].r>>1;if(x<=mid) modify(u<<1,x,c);else modify(u<<1|1,x,c);pushup(u);}
}
int query(int u,int l,int r)
{if(tr[u].l>=l&&tr[u].r<=r) return tr[u].mx;int mid=tr[u].l+tr[u].r>>1;if(l>mid) return query(u<<1|1,l,r);else if(r<=mid) return query(u<<1,l,r);else return max(query(u<<1,l,r),query(u<<1|1,l,r));
}
int main()
{int last=0,n=0;scanf("%d%d",&m,&p);build(1,1,m);while(m--){char op[2];int a;scanf("%s%d",op,&a);if(op[0]=='A'){a=((long long)last+a)%p;modify(1,++n,a);}else {last=query(1,n-a+1,n);cout<<last<<endl;}}
}

ps:修改单点的话就不用pushdown操作了，pushdown需要用到懒标记，有些麻烦，能不用当然更好。 

245. 你能回答这些问题吗（245. 你能回答这些问题吗 - AcWing题库）

这里是单点修改，很容易想到用树状数组来实现，但是树状数组只能维护类似于前缀和这种一整个区间的东西，而我们查询区间中的连续最大子段和，显然用树状数组就没办法实现，那么如果用线段树的话又该怎么实现呢？还是先来看如何定义结构体，显然我们需要储存最大连续子段和，但是这样够不够呢，显然是不够的，因为子节点无法更新父节点，虽然父区间的最大值有可能是左右子区间中的一段，但是还有可能是跨区间的，如果是跨区间的话，要想更新就需要用到左区间的最大后缀和右区间的最大前缀，那么现在就要多维护两个变量——最长前缀和最长后缀，那么现在考虑最长前缀和最长后缀能否能通过子节点来更新父节点，显然是不可以，以最长前缀为例，要用子节点计算的话，有两种情况，一种就是左子节点的最长前缀，一种是左区间加右区间的最大前缀。所以我们实际上还是要维持一个区间和，那么区间和可以由子区间更新父区间吗？当然可以。至此便不用再加别的变量就可以实现这个问题了。

#include<bits/stdc++.h>
using namespace std;
const int N=500010;
int n,m;
int a[N];
struct node{int l,r,mx,lmx,rmx,sum;
}tr[4*N];
void pushup(node &u,node &l,node &r)
{u.mx=max(max(l.mx,r.mx),l.rmx+r.lmx);u.lmx=max(l.lmx,l.sum+r.lmx);u.rmx=max(r.rmx,r.sum+l.rmx);u.sum=l.sum+r.sum;
}
void pushup(int u)
{pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}
void build(int u,int l,int r)
{if(l==r) tr[u]={l,r,a[l],a[l],a[l],a[l]};else{tr[u]={l,r};int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);}
}
void modify(int u,int x,int v)
{if(tr[u].l==x&&tr[u].r==x) tr[u]={x,x,v,v,v,v};else{int mid=tr[u].l+tr[u].r>>1;if(x<=mid) modify(u<<1,x,v);else modify(u<<1|1,x,v);pushup(u);}
}
node query(int u,int l,int r)
{if(l<=tr[u].l&&tr[u].r<=r) return tr[u];int mid=tr[u].l+tr[u].r>>1;if(l>mid) return query(u<<1|1,l,r);else if(r<=mid) return query(u<<1,l,r);else{auto left=query(u<<1,l,r),right=query(u<<1|1,l,r);node res;pushup(res,left,right);return res;}
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);build(1,1,n);while(m--){int op,a,b;scanf("%d%d%d",&op,&a,&b);if(op==1)//最大子段和{if(a>b)swap(a,b);cout<<query(1,a,b).mx<<endl;}else//将a[x]改成y{modify(1,a,b);}}
}

246. 区间最大公约数（246. 区间最大公约数 - AcWing题库）

这里虽然需要修改最大区间，但是修改操作是将区间整体加上一个数，这里可以用差分来处理一下进而避免区间修改操作，毕竟区间修改还怪麻烦的，那么具体该怎么实现呢？维护差分是很容易的，问题在于如何维护gcd的值，这里需要用到欧几里得算法,我们简单证明一下：

gcd(a1,a2,a3,...,an)=gcd(a1,a2-a1,a3-a2,...)

令g=gcd(a1,a2,a3...);

那么a1%g=0,a2%g=0,a3%g=0,...

故而(a2-a1)%g=0,(a3-a2)%g=0,...

故而gcd(a1,a1-a2,a2-a3,...)>=g（gcd(a1,a2-a1,a3-a2,...)是最大公因数，g是一个因数，所以满足大于等于的关系）

令g=gcd(a1,a2-a1,a3-a2,...),

那么a1%g=0,(a2-a1)%g=0,所以a2%g=0,以此类推，a3%g=0,...

故而gcd(a1,a2,a3,...,an)>=g
所以gcd(a1,a2,a3,...,an)=gcd(a1,a2-a1,a3-a2,...)

差分数组是什么呢：
b1=a1-a0

b2=a2-a1

...

所以我们可以通过维护差分数组来实现。

 然后如果需要获得gcd需要维护哪些值呢？gcd(sum(1~bl),gcd(b[l+1],...,b[r]))
区间和这个很容易得到，那么后面的gcd(b[l+1],...,b[r])怎么得到呢，显然如果维和子区间的gcd的话，可以用子区间的gcd得到父区间的gcd，所以就只需要维护区间的gcd和sum即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=500010;
int n,m;
long long a[N];
struct node{int l,r;ll sum,g;
}tr[4*N];
ll gcd(ll a,ll b)
{return b?gcd(b,a%b):a;
}
void pushup(node &u,node &l,node &r)
{u.sum=l.sum+r.sum;u.g=gcd(l.g,r.g);
}
void pushup(int u)
{pushup(tr[u],tr[u<<1],tr[u<<1|1]);
}
void build(int u,int l,int r)
{if(l==r) {ll b=a[r]-a[r-1];tr[u]={l,r,b,b};}else{tr[u].l=l,tr[u].r=r;int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);}
}
void modify(int u,int x,ll v)
{if(tr[u].l==x&&tr[u].r==x) {ll b=tr[u].sum+v;tr[u]={x,x,b,b};}else{int mid=tr[u].l+tr[u].r>>1;if(x<=mid) modify(u<<1,x,v);else modify(u<<1|1,x,v);pushup(u);}
}node query(int u,int l,int r)
{if(l<=tr[u].l&&tr[u].r<=r) return tr[u];int mid=tr[u].l+tr[u].r>>1;if(l>mid) return query(u<<1|1,l,r);else if(r<=mid) return query(u<<1,l,r);//一定要记得写returnelse{auto left=query(u<<1,l,r),right=query(u<<1|1,l,r);node res;pushup(res,left,right);return res;}
}int main()
{scanf("%d%d",&n,&m);a[0]=0;for(int i=1;i<=n;i++) scanf("%lld",&a[i]);build(1,1,n);while(m--){char op[2];int l,r;scanf("%s%d%d",op,&l,&r);if(op[0]=='Q'){auto left = query(1, 1, l);node right({0,0,0,0});if(l+1<=r) right=query(1,l+1,r);cout<<abs( gcd(left.sum,right.g) )<<endl;}else{long long v;scanf("%lld",&v);modify(1,l,v);if(r+1<=n)modify(1,r+1,-v);}}
}

243. 一个简单的整数问题2（活动 - AcWing）

这里是给一段区间同时加上一个数，也很容易想到能不能用差分代替区间修改，但是我们如果用线段树维护差分数组的话，没有办法快速获得区间和，所以这里无可避免的需要实现区间修改，那么就要用到pushdown操作了。

pushdown的操作虽然麻烦，但实际上思路还是比较容易的。 我们在定义区间节点的时候实际上还定义了一个懒标记，对区间进行修改，那么我们我们如果搜到的区间如果被包含在目标区间中，那么我们就将这个区间节点中的懒标记修改一下，然后返回不再往下搜了，如果不完全包含的话，就先将当前搜到区间的懒标记先传下去，然后再执行进一步的递归。这里将懒标记传下去的操作就是pushdown，那么pushdown具体怎么实现呢，实际还要回到懒标记的意义上来，懒标记意味着从当前区间往下所有的区间都需要进行这个修改，当前区间是否执行这个修改无所谓，目的是将修改传到叶子节点，然后由叶子节点往上更新来实现。我们这里定义的话，就直接将修改加到区间上，懒标记表示下面的需要进行的修改。

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int a[N];
int n,m;
struct node
{int l,r;long long sum,add;
}tr[4*N];
void pushup(int u)
{tr[u].sum = tr[u<<1].sum+tr[u<<1|1].sum;
}
void pushdown(int u)
{tr[u<<1].add+=tr[u].add,tr[u<<1].sum += (long long)(tr[u<<1].r-tr[u<<1].l+1)*tr[u].add;tr[u<<1|1].add+=tr[u].add,tr[u<<1|1].sum += (long long)(tr[u<<1|1].r-tr[u<<1|1].l+1)*tr[u].add;tr[u].add=0;
}
void build(int u,int l,int r)
{if(l==r) tr[u]={l,r,a[l],0};else{tr[u]={l,r};int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);}
}
void modify(int u,int l,int r,int v)
{if(l<=tr[u].l&&tr[u].r<=r) {tr[u].sum += (long long)(tr[u].r-tr[u].l+1)*v;tr[u].add+=v;}else{pushdown(u);int mid=tr[u].l+tr[u].r>>1;if(r<=mid) modify(u<<1,l,r,v);else if(l>mid) modify(u<<1|1,l,r,v);else modify(u<<1,l,r,v),modify(u<<1|1,l,r,v);pushup(u);}
}
long long query(int u,int l,int r)
{if(l<=tr[u].l&&tr[u].r<=r) return tr[u].sum;pushdown(u);int mid=tr[u].l+tr[u].r>>1;long long v=0;if(l<=mid) v+=query(u<<1,l,r);if(r>mid) v += query(u<<1|1,l,r);return v;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&a[i]);build(1,1,n);while(m--){char op[2];int l,r;scanf("%s%d%d",op,&l,&r);if(op[0]=='Q'){cout<<query(1,l,r)<<endl;}else{int v;scanf("%d",&v);modify(1,l,r,v);}}
}

247. 亚特兰蒂斯（247. 亚特兰蒂斯 - AcWing题库）

图差不多是这个样子， 

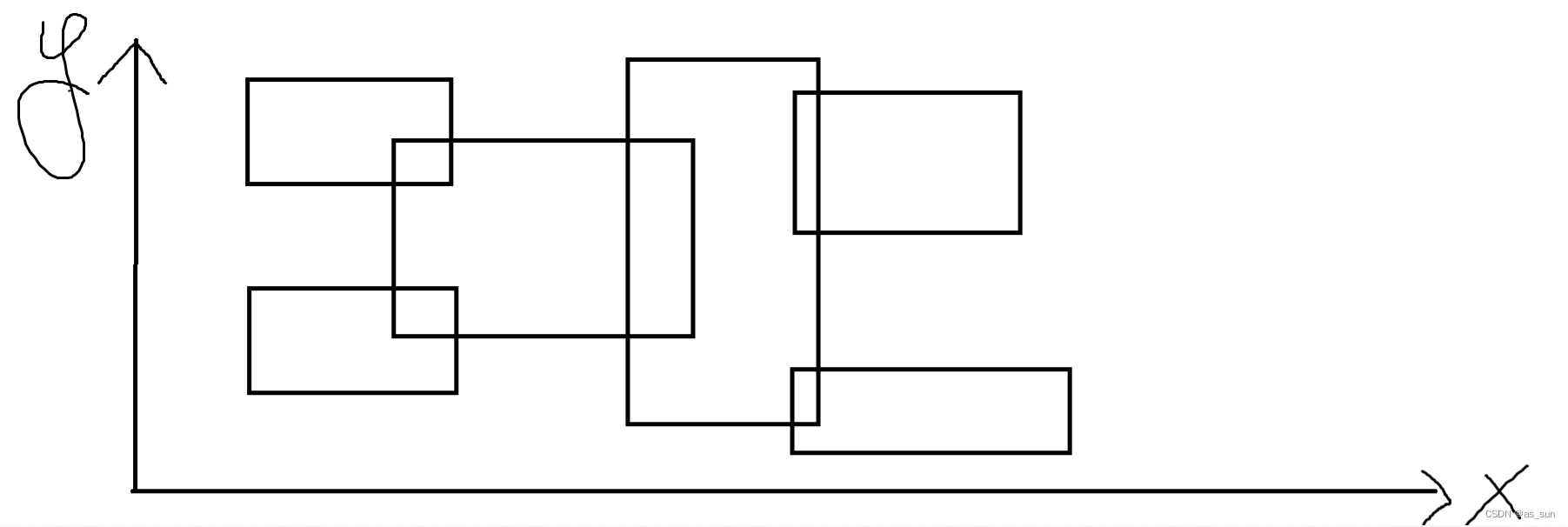
单个算还好说，重叠起来就很麻烦。所以这里引入一种全新的算法——扫描线：

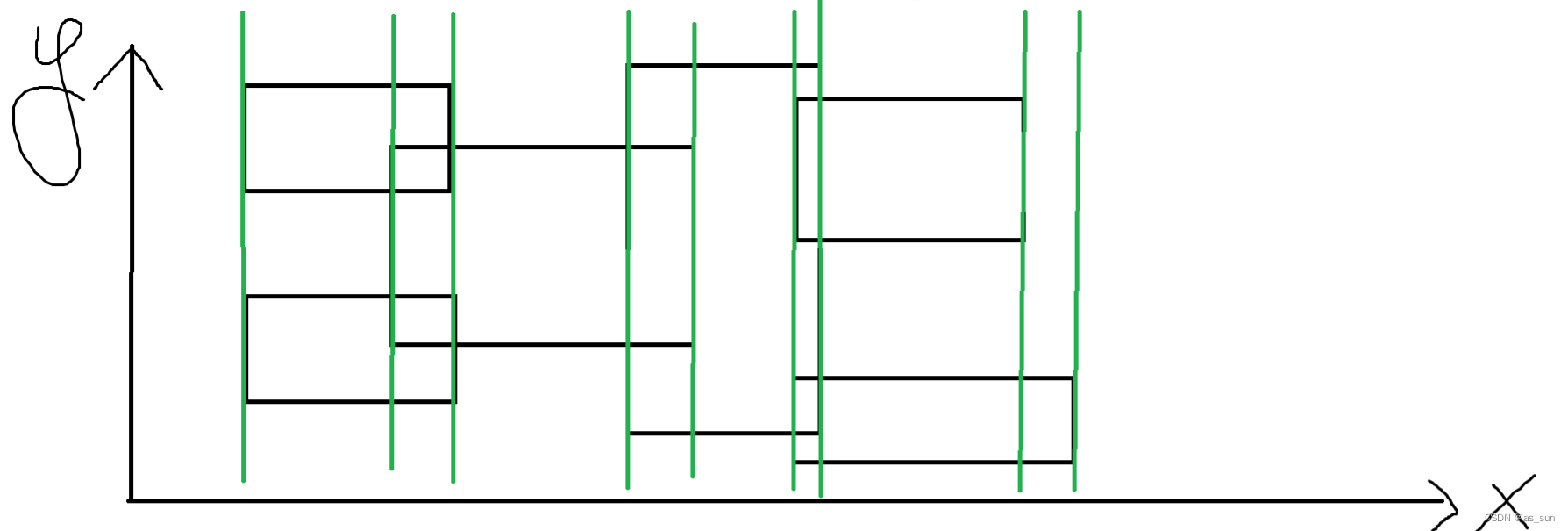
我们将图分成如上的区间，显然在一个区间中面积就是区间长度(横坐标差)*区间中纵坐标覆盖的总长度。 假设有一根无限长的直线进行扫描，显然当一个矩形最左边的边被扫到的时候，那么就要开始计算面积了，第二次被扫到的时候就不能再计算这个矩形了。这里我们可以通过对这段区间标记来处理，令左边的标记为1，右边的标记为-1，那么刚好扫到右边的时候就不用再考虑它了。

 区间长度倒是还比较好获得，问题在于纵坐标覆盖的总长度该怎么看，显然在一个区间中它是不变的，那么我们可以一个区间一个区间地往后看。那么该如何维护呢？这里有个特别妙地思路，因为y是浮点数，所以需要对y进行离散化，而且我们用线段树维护的时候也并非用区间的端点维护区间，而是在离散化后，得到若干个点，每两点之间的区间我们给它定一个序号，然后我们用线段树的节点来维护每一个区间的序号，这样说还是有点抽象，见下图：

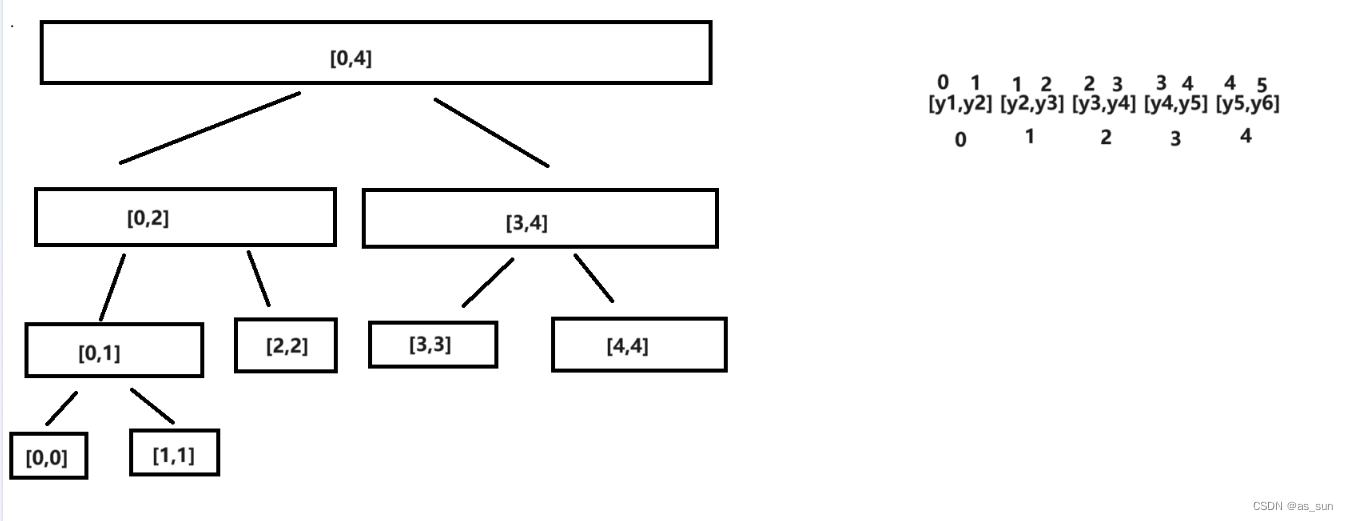
我们看叶子节点，每个叶子节点维护的实际是一个对应序号的区间。

然后再来考虑我们具体需要维护的值是什么，首先我们要直到区间是否被标记才能进一步考虑是否需要把这段长度算上，那么很显然我们需要一个cnt来标记这段区间的标记情况，又因为一个矩形的左右边是对称的，所以cnt的值恒大于等于0，如果cnt>0，那么这段区间就会被考虑，如果cnt==0，那么这段区间就不能再被考虑。

然后需要一个变量len来维护这段区间中被标记部分的总长度。 

由于线段树维护的是区间的序号，所以我们每次用到的只有根节点的len，所以在更新的时候，我们是会把cnt传到完全包含的区间部分去的。而且我们每次用的都是根节点的值，所以只要它往上传是正确的，那么就无所谓，所以我们并不需要将父节点的cnt传到子节点去，只要保证子节点的cnt被更新后将len的变化传到父节点去即可。所以一个节点被标记的意义就是这个节点能被表示的所有区间都被标记。

所以在pushup的时候，
如果父节点被标记，那么父节点的len自己用两端点更新一下就好（所以我们更新区间的时候就需要pushup，因为cnt发生了变化）；
如果父节点没有被标记，那么就要看它是不是叶子节点，
如果是叶子节点那么len就是0，
否则就需要用它的子节点来更新一下它，因为cnt可能传到它的子节点上去了。

所以我们是先递归然后再进行pushup，这样才能实现从子节点往上在回溯的过程中更新父节点。至此本题相较于模板特殊的地方都讨论完了。

然后这里的离散化就用vector就行，然后查找用二分。

另外需要记录一下左右边。

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
struct edge{double x,y1,y2;int sta;
}seg[2*N];//每个矩形记录左右边
struct node{int l,r,cnt;double len;
}tr[8*N];//4*2*N
bool cmp(edge a,edge b)
{return a.x<b.x;
}
int n;
vector<double>hy;//对y进行离散化
void pushup(int u)
{if(tr[u].cnt) tr[u].len=hy[tr[u].r+1]-hy[tr[u].l];else if(tr[u].l!=tr[u].r){tr[u].len=tr[u<<1].len+tr[u<<1|1].len;}else{tr[u].len=0;}
}
void build(int u,int l,int r)
{tr[u]={l,r,0,0};if(l==r) return;int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);
}
void modify(int u,int l,int r,int k)
{if(l<=tr[u].l&&tr[u].r<=r) {tr[u].cnt+=k;pushup(u);}else{int mid=tr[u].l+tr[u].r>>1;if(l<=mid) modify(u<<1,l,r,k);if(r>mid) modify(u<<1|1,l,r,k);pushup(u);}
}
int find(double x)
{return lower_bound(hy.begin(),hy.end(),x)-hy.begin();
}
int main()
{int t=0;while(~scanf("%d",&n)){hy.clear();t++;if(!n) break;int j=0;for(int i=1;i<=n;i++){double x1,y1,x2,y2;scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);seg[j++]={x1,y1,y2,1},seg[j++]={x2,y1,y2,-1};hy.push_back(y1),hy.push_back(y2);}sort(hy.begin(),hy.end());hy.erase(unique(hy.begin(),hy.end()),hy.end());build(1,0,hy.size()-2);sort(seg,seg+2*n,cmp);double res=0;for(int i=0;i<2*n;i++){if(i) res += (seg[i].x-seg[i-1].x)*tr[1].len;modify(1,find(seg[i].y1),find(seg[i].y2)-1,seg[i].sta);}printf("Test case #%d\n",t);printf("Total explored area: %.2lf\n",res);printf("\n");}
}

1277. 维护序列(活动 - AcWing)

思路：这里和之前不同的地方就在不仅要对一段区间同时加上一个数，还要对一段区间同时乘上一个数，所以就涉及到先后顺序的问题了，所谓先后怎么说呢，实际上是父节点去更新子节点的时候对子节点产生的先后。因为子节点本身是有更新的，那么它被父节点更新的时候是先加还是先乘呢：

我们来分别讨论，如果是先加再乘：

(x+a)*b

那么父节点的懒标记传过来的时候，哪怕只有加c

(x+a)*b+c

是没有办法变成（x+_）*_的形式的，所以先加再乘不合适

那么如果是先乘再加呢：

x*b+a

父节点的懒标记传过来的时候：

x*b+a+c

(x*b+a)*mul=x*b*mul+a*mul

都是可以变成x*_+_的形式的，所以我们就定义先乘再加。

那么更新的时候既有乘的操作又有加的操作，实际上还是有点麻烦的，所以我们这么来，如果是加x的话就定义成*1和+x）, 如果是*x的话就定义成*x和+0.这样写一个modify函数就够了。

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
typedef long long ll;
int a[N];
int n,m,p;
struct node{int l,r;int sum,add,mul;
}tr[4*N];
void pushup(int u)
{tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%p;
}
//(x*a+b)*c+d=x*a*c+b*c+d
void eval(node &u,int mul,int add)
{u.sum=((ll)u.sum*mul+(ll)(u.r-u.l+1)*add)%p;u.add=((ll)u.add*mul+add)%p;u.mul=(ll)u.mul*mul%p;
}
void pushdown(int u)
{eval(tr[u<<1],tr[u].mul,tr[u].add);eval(tr[u<<1|1],tr[u].mul,tr[u].add);tr[u].add=0,tr[u].mul=1;
}
void build(int u,int l,int r)
{if(l==r) tr[u]={l,r,a[l],0,1};else{tr[u]={l,r,0,0,1};//反正子节点还要来更新它的int mid=l+r>>1;build(u<<1,l,mid),build(u<<1|1,mid+1,r);pushup(u);}
}
void modify(int u,int l,int r,int mul,int add)
{if(l<=tr[u].l&&tr[u].r<=r) {eval(tr[u],mul,add);}else{pushdown(u);int mid=tr[u].l+tr[u].r>>1;if(l<=mid) modify(u<<1,l,r,mul,add);if(r>mid) modify(u<<1|1,l,r,mul,add);pushup(u);}
}
int query(int u,int l,int r)
{if(l<=tr[u].l&&tr[u].r<=r) return tr[u].sum;pushdown(u);int mid=tr[u].l+tr[u].r>>1;int v=0;if(l<=mid) v=query(u<<1,l,r);if(r>mid) v=(v+query(u<<1|1,l,r))%p;return v;
}
int main()
{scanf("%d%d",&n,&p);for(int i=1;i<=n;i++) scanf("%d",&a[i]);build(1,1,n);scanf("%d",&m);while(m--){int op,l,r,v;scanf("%d%d%d",&op,&l,&r);if(op==1)//*{scanf("%d",&v);modify(1,l,r,v,0);}else if(op==2)//+{scanf("%d",&v);modify(1,l,r,1,v);}else//q{cout<<query(1,l,r)<<endl;}}
}