LeetCode 2368.受限条件下可到达节点的数目：搜索 + 哈希表-编程知识

LeetCode 2368.受限条件下可到达节点的数目：搜索 + 哈希表

【LetMeFly】2368.受限条件下可到达节点的数目：搜索 + 哈希表

力扣题目链接：https://leetcode.cn/problems/reachable-nodes-with-restrictions/

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [a_i, b_i] 表示树中节点 a_i 和 b_i 之间存在一条边。另给你一个整数数组 restricted 表示受限节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的最多节点数目。

注意，节点 0 不会标记为受限节点。

示例 1：

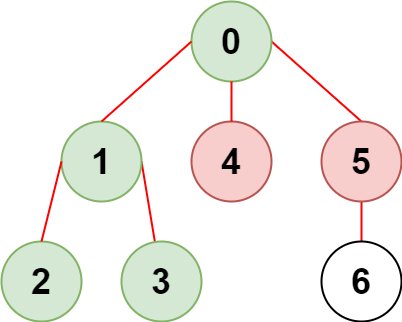
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

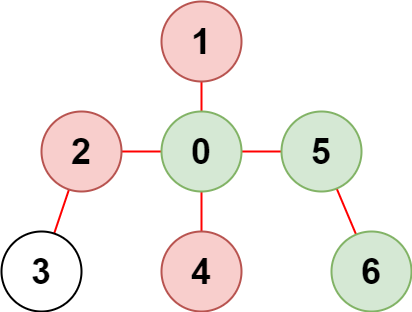
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

提示：

2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges 表示一棵有效的树
1 <= restricted.length < n
1 <= restricted[i] < n
restricted 中的所有值 互不相同

方法一：深度优先搜索(DFS)

首先开辟一个大小为 $n\times 0$ 的二维数组graph，graph[i]表示所有与节点i相邻的边（遍历edges数组即可完成建图）。

接着使用一个哈希表用来记录不可达节点（遍历restricted数组可以完成哈希表的初始值）。若一个节点被遍历过后，也可将其标记为不可达。

之后就能从节点0开始愉快地搜索了（每次搜索时先将该节点标记并将答案数量加一，再递归所有未被标记过的邻居节点）。

时间复杂度 $O (n)$
空间复杂度 $O (n)$

AC代码

C++

class Solution {
private:int ans;unordered_set<int> unachieveable;vector<vector<int>> graph;void dfs(int n) {unachieveable.insert(n);ans++;for (int next : graph[n]) {if (!unachieveable.count(next)) {dfs(next);}}}
public:int reachableNodes(int n, vector<vector<int>>& edges, vector<int>& restricted) {ans = 0;graph.resize(n);for (vector<int>& edge : edges) {graph[edge[0]].push_back(edge[1]);graph[edge[1]].push_back(edge[0]);}for (int t : restricted) {unachieveable.insert(t);}dfs(0);return ans;}
};

Python

from typing import Listclass Solution:def dfs(self, n: int) -> None:self.unachieveable.add(n)self.ans += 1for next in self.graph[n]:if next not in self.unachieveable:self.dfs(next)def reachableNodes(self, n: int, edges: List[List[int]], restricted: List[int]) -> int:self.ans = 0self.graph = [[] for _ in range(n)]for x, y in edges:self.graph[x].append(y)self.graph[y].append(x)self.unachieveable = set(restricted)self.dfs(0)return self.ans