运筹学_1.2线性规划问题的几何意义
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/505772.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
基于springboot+vue的流浪宠物管理系统
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、阿里云专家博主、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战,欢迎高校老师\讲师\同行交流合作 主要内容:毕业设计(Javaweb项目|小程序|Pyt…
Ubuntu将c++编译成.so文件并测试
一、准备cpp和h文件
创建test.cpp
在cpp中定义相加的函数funcAdd,给出函数的细节代码
#include <iostream>
using namespace std;int funcAdd(int x, int y)
{return xy;
}创建test.h
在h中声明定义的函数,不需要任何细节
#ifndef __TEST__
#…
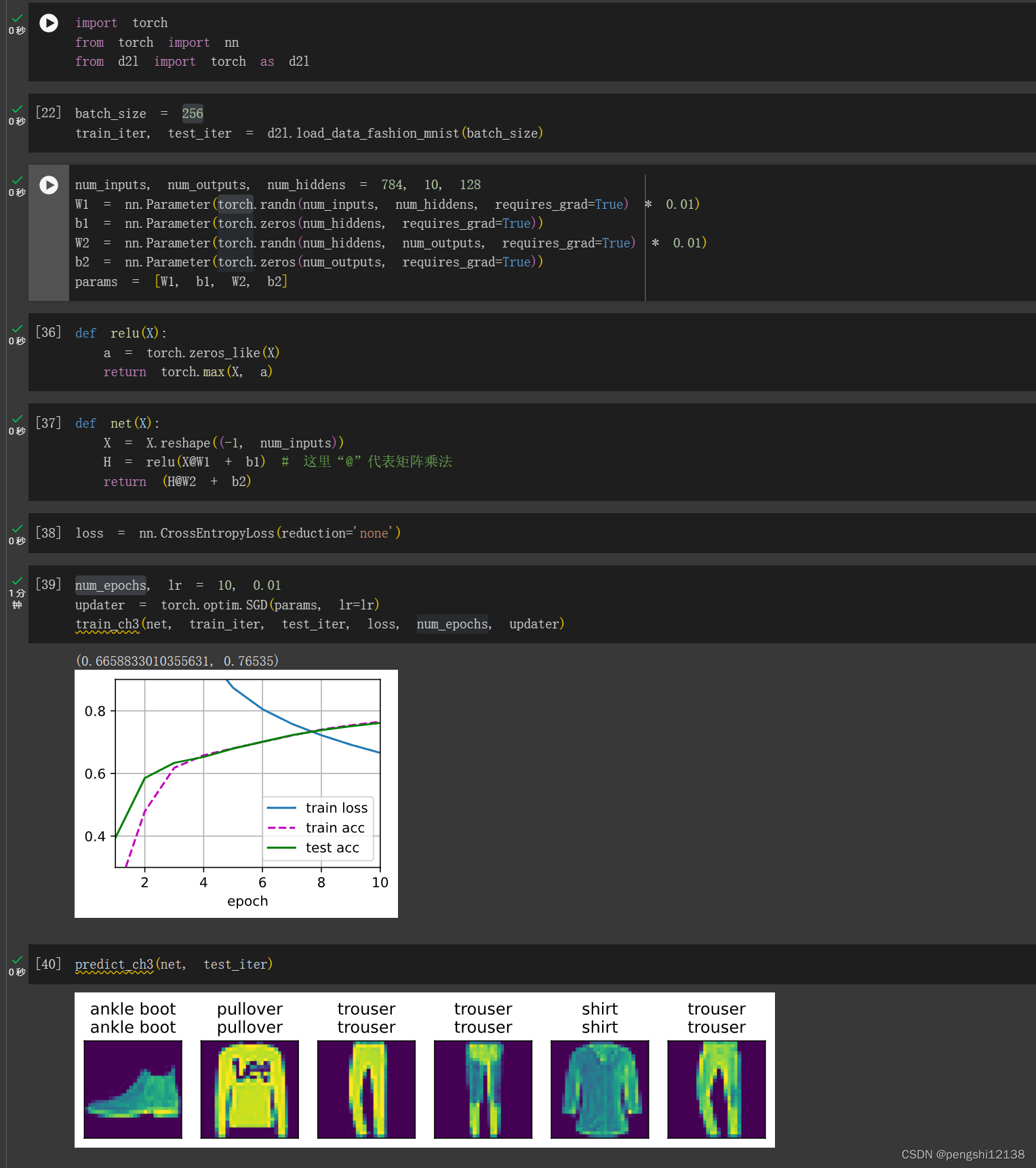
李沐动手学习深度学习——4.2练习
1. 在所有其他参数保持不变的情况下,更改超参数num_hiddens的值,并查看此超参数的变化对结果有何影响。确定此超参数的最佳值。
通过改变隐藏层的数量,导致就是函数拟合复杂度下降,隐藏层过多可能导致过拟合,而过少导…
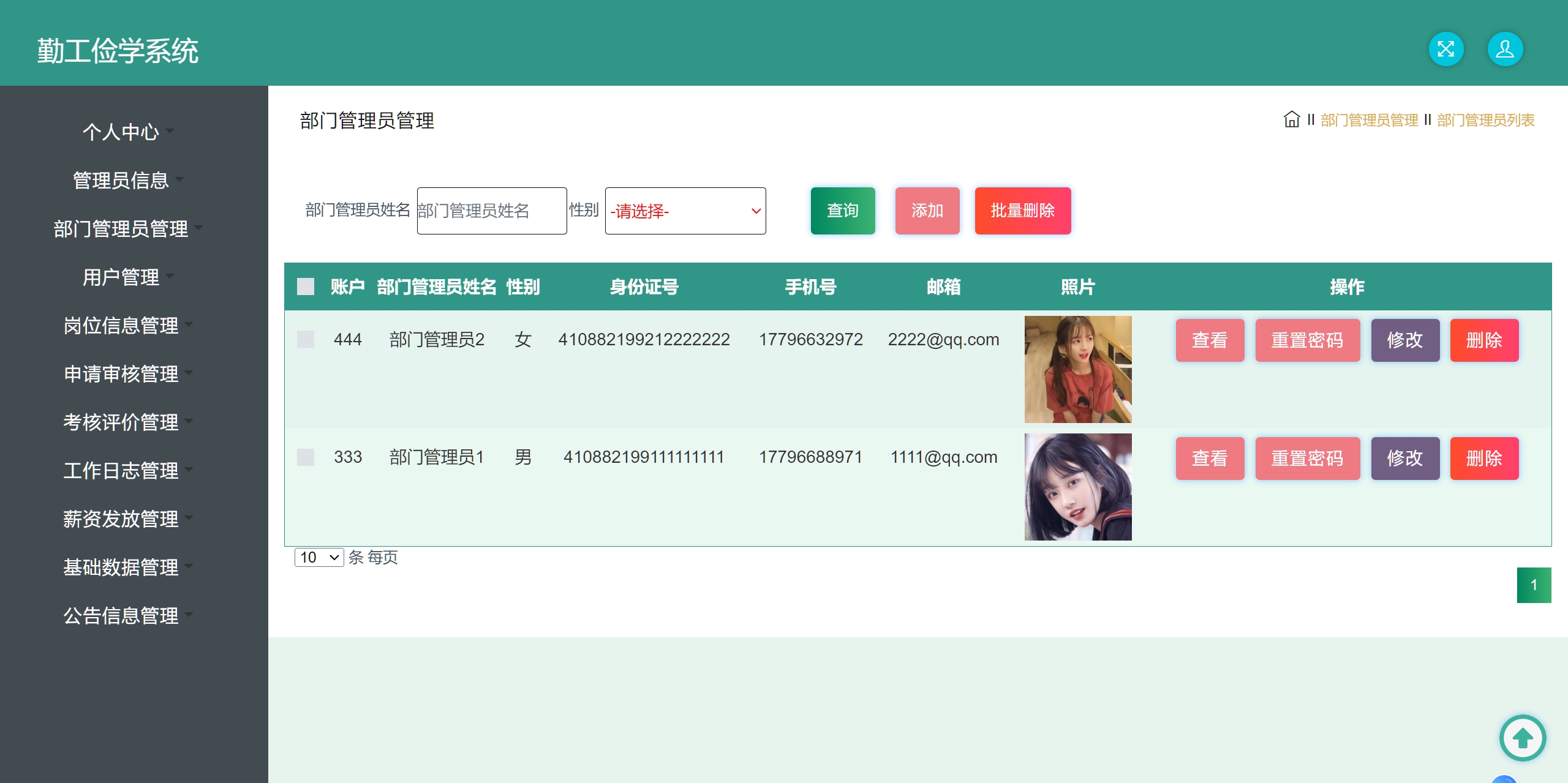
Java项目:31 基于SSM的勤工俭学管理系统
作者主页:源码空间codegym 简介:Java领域优质创作者、Java项目、学习资料、技术互助 文中获取源码 项目介绍
勤工助学系统有管理员,部门管理员,用户三个角色。
管理员功能有个人中心。管理员管理,部门管理员管理&…
鸿蒙Harmony应用开发—ArkTS声明式开发(通用属性:Popup控制)
给组件绑定popup弹窗,并设置弹窗内容,交互逻辑和显示状态。 说明: 从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版本。 popup弹窗的显示状态在onStateChange事件回调中反馈,其显…
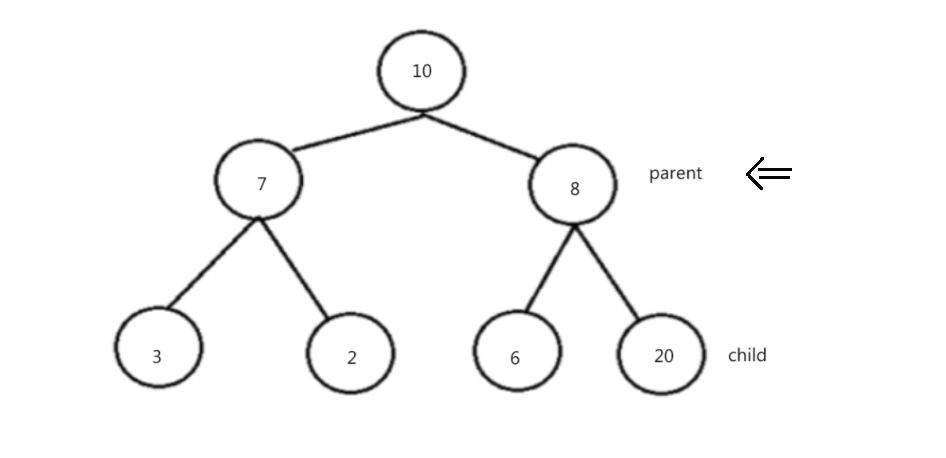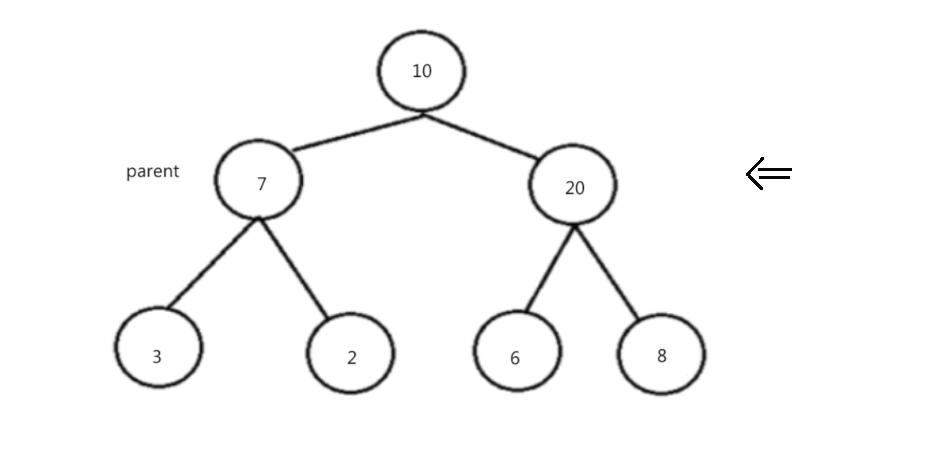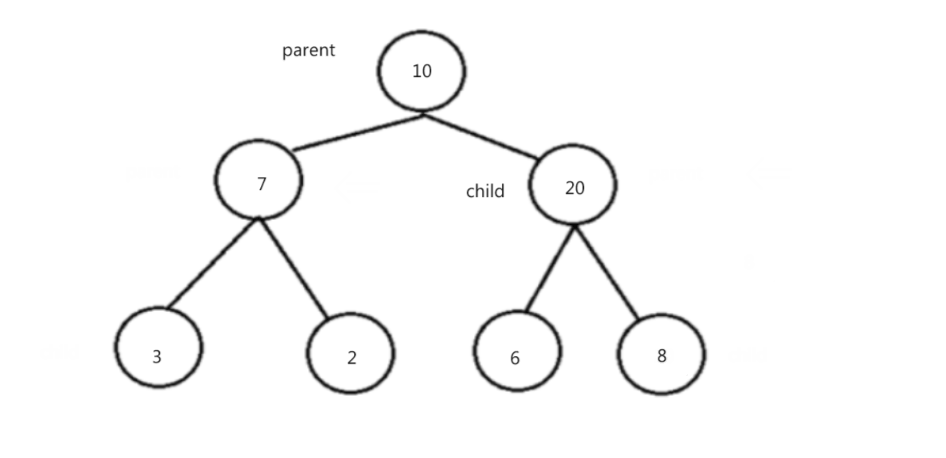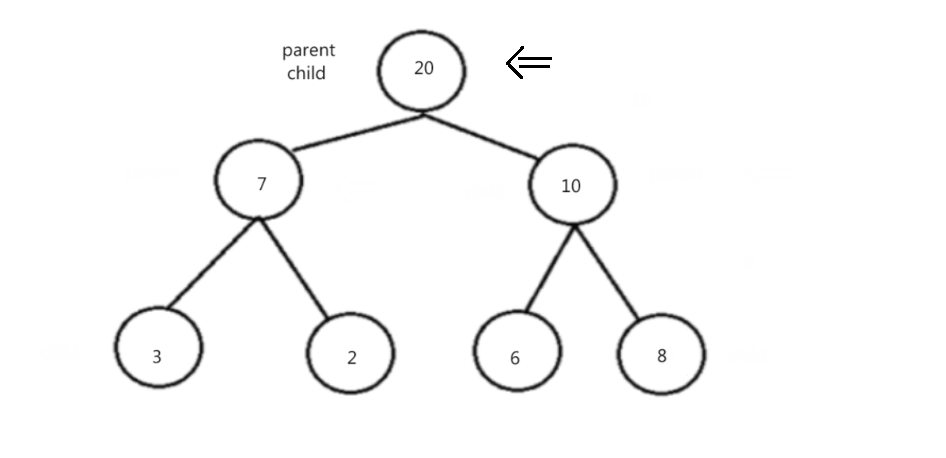
初阶数据结构:二叉树
目录 1. 树的相关概念1.1 简述:树1.2 树的概念补充 2. 二叉树2.1 二叉树的概念2.2 二叉树的性质2.3 二叉树的存储结构与堆2.3.1 存储结构2.3.2 堆的概念2.3.3 堆的实现2.3.3.1 堆的向上调整法2.3.3.2 堆的向下调整算法2.3.3.3 堆的实现 1. 树的相关概念
1.1 简述&a…
MyBatis 学习(六)之动态 SQL
目录
1 动态 SQL 介绍
2 if 标签
3 where 标签
4 set 标签
5 trim 标签
6 choose、when、otherwise 标签
7 foreach 标签
8 bind 标签 1 动态 SQL 介绍 动态 SQL 是 MyBatis 强大特性之一,极大的简化我们拼装 SQL 的操作。MyBatis 的动态 SQL 是基于 OGNL 的…
网络编程(IP、端口、协议、UDP、TCP)【详解】
目录
1.什么是网络编程?
2.基本的通信架构
3.网络通信三要素
4.UDP通信-快速入门
5.UDP通信-多发多收
6.TCP通信-快速入门
7.TCP通信-多发多收
8.TCP通信-同时接收多个客户端
9.TCP通信-综合案例 1.什么是网络编程? 网络编程是可以让设…
【Vue3】PostCss 适配
px 固定的单位,不会进行自适应。rem r root font-size16px 1rem16px,但是需要手动进行单位的换算vw vh 相对于视口的尺寸,不同于百分比(相对于父元素的尺寸)375屏幕 1vw 3.75px
利用插件进行 px(设计稿&…
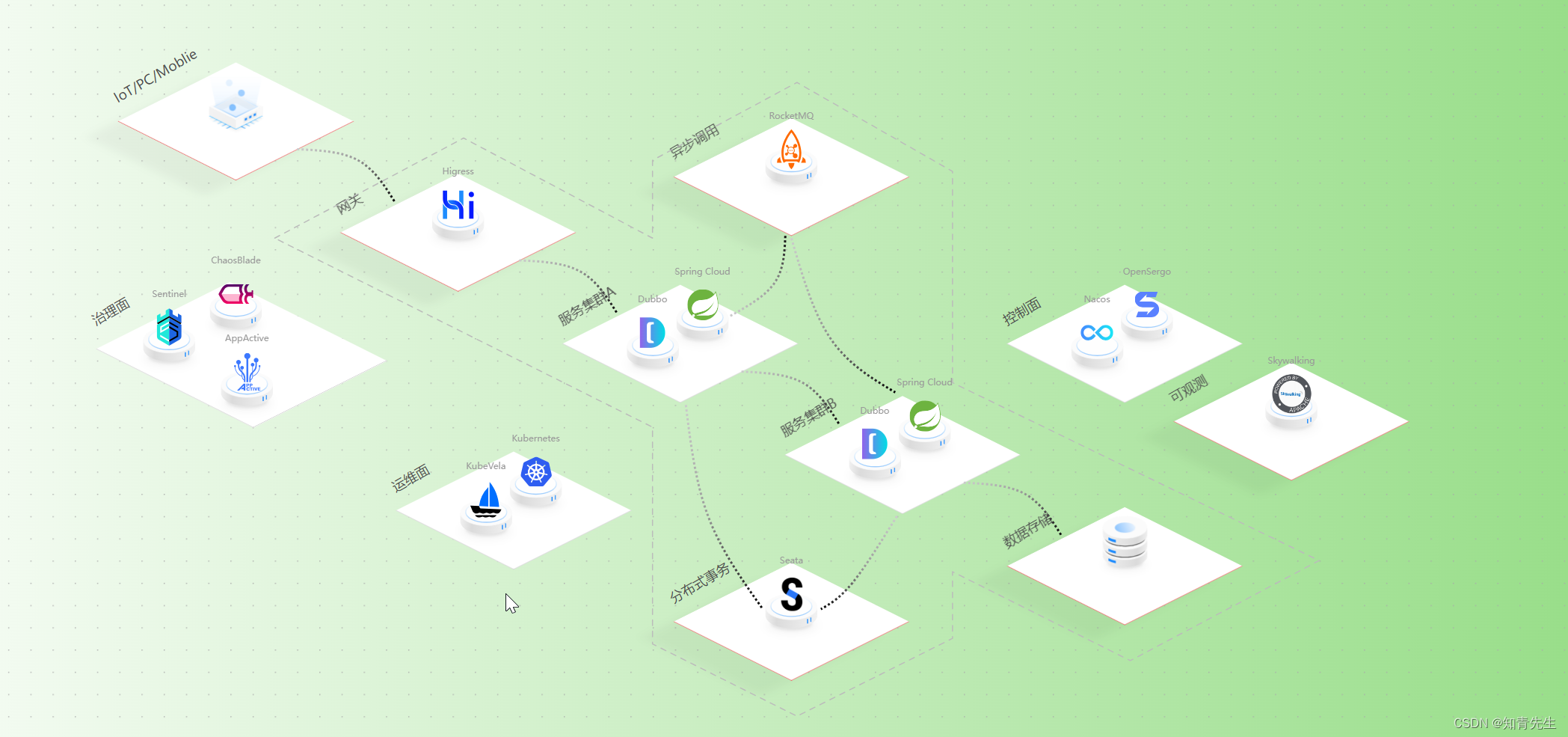
SpringCloudAlibaba介绍
Spring Cloud Alibaba Spring Cloud Alibaba 是什么?微服务全景图核心特色 大家好,我叫阿明。下面我会为大家准备Spring Cloud Alibaba系列知识体系,结合实战输出案列,让大家一眼就能明白得技术原理,应用于各公司得各…
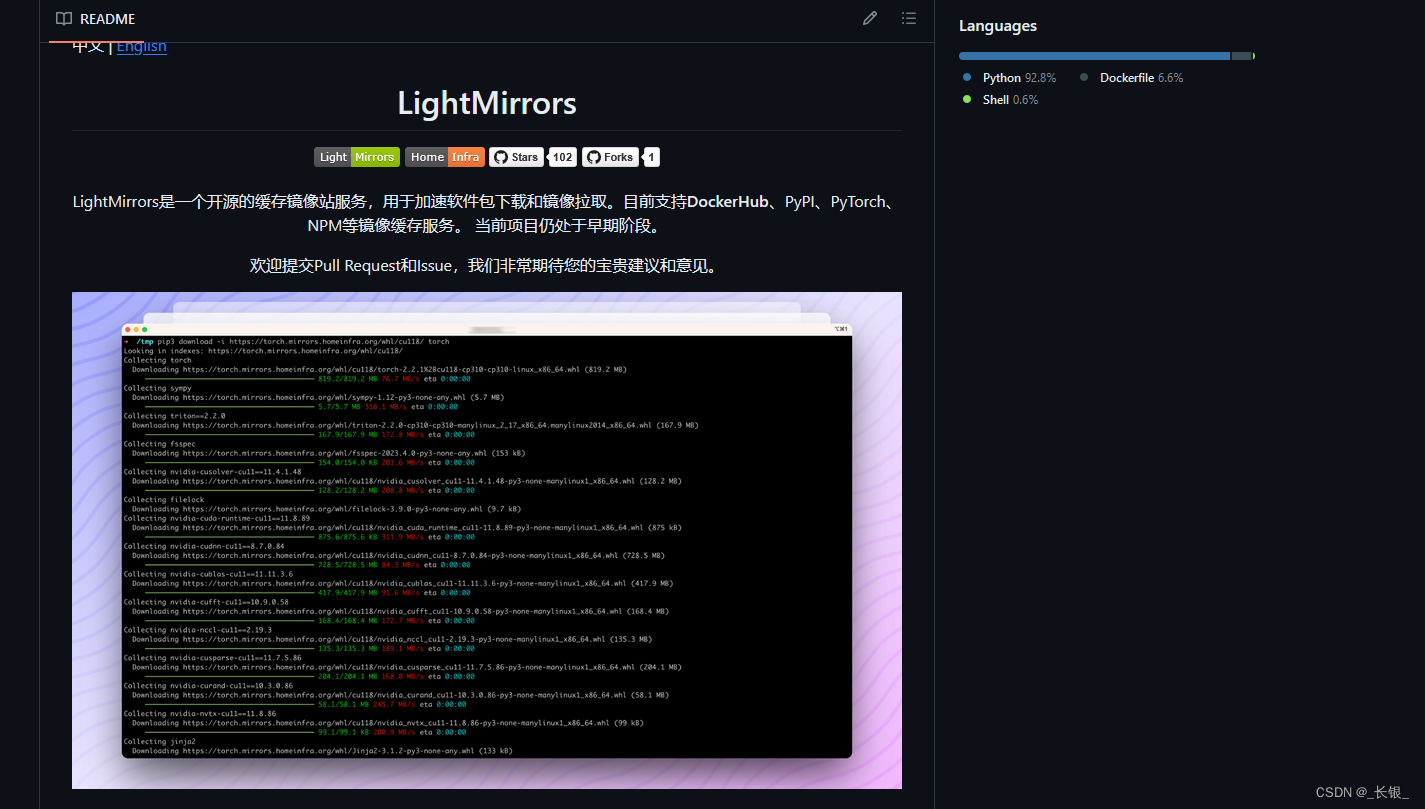
Github项目推荐-LightMirrors
项目地址
https://github.com/NoCLin/LightMirrors
项目简述
“LightMirrors是一个开源的缓存镜像站服务,用于加速软件包下载和镜像拉取。目前支持DockerHub、PyPI、PyTorch、NPM等镜像缓存服务。 当前项目仍处于早期阶段。”–来自项目说明。 也就是说ÿ…
如何解决线程安全问题(synchronized、原子性、产生线程不安全的原因,锁的特性,加锁的方式等等干货)
文章目录 💐线程不安全的示例💐锁的特性💐产生线程不安全的原因:💐加锁的三种方式 💐线程不安全的示例
对于线程安全问题,这里用一个例子进行讲解👇:
我现在定义一个变…