Day 38

01. 不同路径（No. 62）

题目链接

代码随想录题解

<1> 题目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

<2> 笔记

在尝试使用递归去解题的时候，先去尝试确定一个可以转移的 状态

题目中问的是共有多少条路径，那是不是可以尝试将到达某个节点的方法种数作为状态呢？

再来思考这个状态能否可以转移呢？因为机器人 只能 往下和往右移动，所以到达一个节点的方式是可以依据这个节点的上面和左边推导而来的；这样 状态转移方程 也较为容易的能列出。

既然某个节点的状态需要右边和上面列出，那必须要保证一开始最上面那一行和最左边那一列是初始化的，既然机器人只能 向下 和 向右 移动，那这两列都可以初始化为 1 ，因为到达这两个位置的任意一个节点都只有 一种方法。

那最左上角的节点初始化成什么呢？答案是初始化成什么都可以，因为在遍历其他节点的时候根本用不到这个节点的值！

来用动态规划五部曲总结一下思路：

🍀 dp 数组的含义：到达下表为 [i, j] 的节点有 dp[i][j] 种方法。

🍀 确定递推公式：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]，即到达一个节点的方法等于到达这个节点上方的节点的方法加上到达这个节点左方的方法加和。

🍀 dp 数组的初始化：和上面提到的相同

🍀 确定遍历顺序：因为某个节点的结果需要上方和左方的推导，所以遍历顺序是从上到下，从左到右的。

🍀 举例推导 dp 数组

<3> 代码

class Solution {public int uniquePaths(int m, int n) {int[][] map = new int[m][n];for (int i = 0; i < n; i++) {map[0][i] = 1;}for (int i = 0; i < m; i++) {map[i][0] = 1;}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {map[i][j] = map[i - 1][j] + map[i][j - 1];}}return map[m - 1][n - 1];}
}

02. 不同路径（No. 63）

题目链接

代码随想录题解

<1> 题目

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

• m == obstacleGrid.length
• n == obstacleGrid[i].length
• 1 <= m, n <= 100
• obstacleGrid[i][j] 为 0 或 1

<2> 笔记

有了上题的经验思考本题就变得容易了许多，本题在原本的基础上加上了 阻碍 这个特性，但其实对 整体的思路 是没有影响的，这也就代表了 dp 数组的 含义 不需要再去重新确认。

那这道题只需要思考这个阻碍物对 dp 数组的初始化会不会有影响呢？机器人只能往右边和往下面走，所以最左边那一列一旦出现了阻碍，那剩余的部分均是无法到达的。

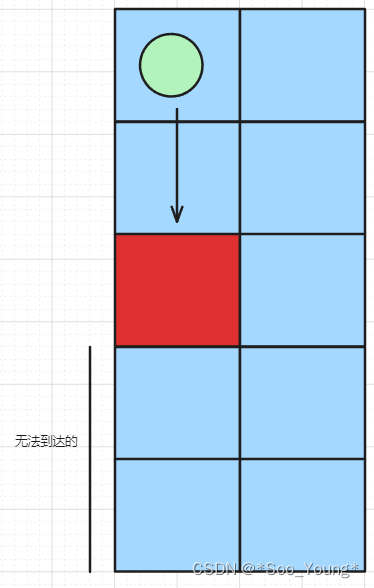
所以如果这一条路径上出现了阻碍，剩余的部分 应该全部初始化为 0。

		for (int i = 0; i < m; i++) {if (obstacleGrid[i][0] == 0) {map[i][0] = 1;} else {break; // 直接 break 出去，剩余的部分就不赋值为 1 了}}for (int i = 0; i < n; i++) {if (obstacleGrid[0][i] == 0) {map[0][i] = 1;} else {break;}}

对于状态转移方程也要做一些调整，因为 障碍物永远是不可达的 所以所有障碍物的位置都要变为 0

if (obstacleGrid[i][j] == 0) {
、// 对不为 0 的部分也就是障碍物不做处理，默认为 0map[i][j] = map[i - 1][j] + map[i][j - 1];
}

思考一下已经没有其他的影响了，写出代码。

<3> 代码

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m = obstacleGrid.length;int n = obstacleGrid[0].length;int[][] map = new int[obstacleGrid.length][obstacleGrid[0].length];// dp 数组的初始化for (int i = 0; i < m; i++) {if (obstacleGrid[i][0] == 0) {map[i][0] = 1;} else {break;}}for (int i = 0; i < n; i++) {if (obstacleGrid[0][i] == 0) {map[0][i] = 1;} else {break;}}for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 0) {// 只遍历不为障碍物的部分map[i][j] = map[i - 1][j] + map[i][j - 1];}}}return map[m - 1][n - 1];}
}