解决办法,安装虚拟网卡,win11查找方式:控制面板→网络和共享中心→更改适配器设置
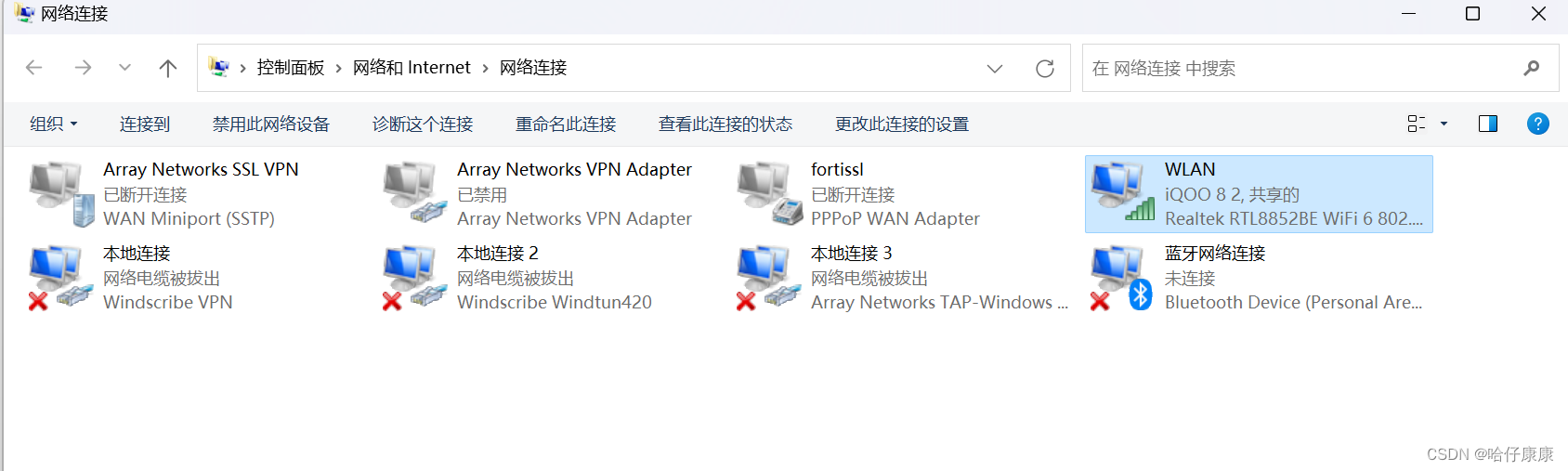
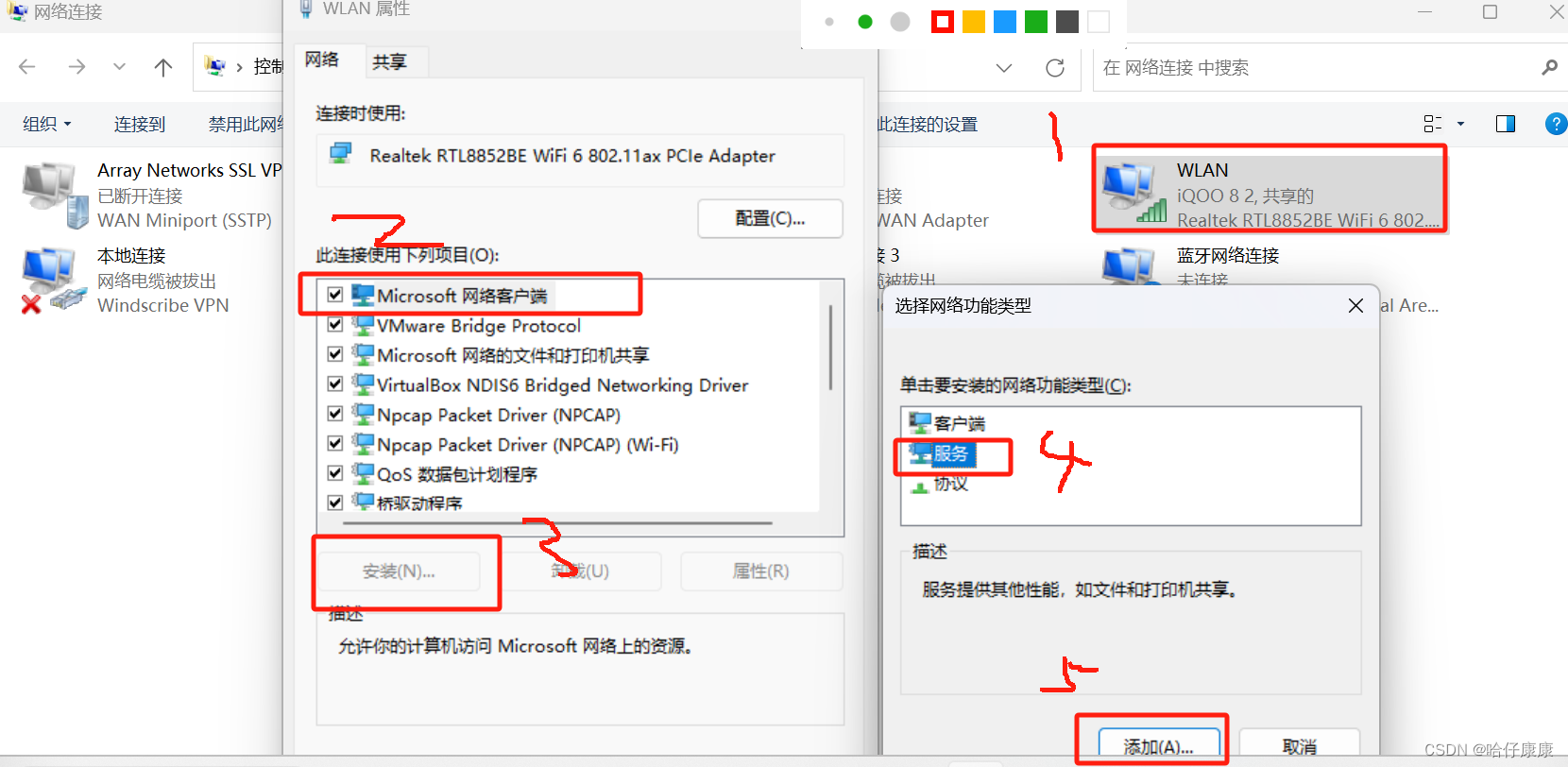

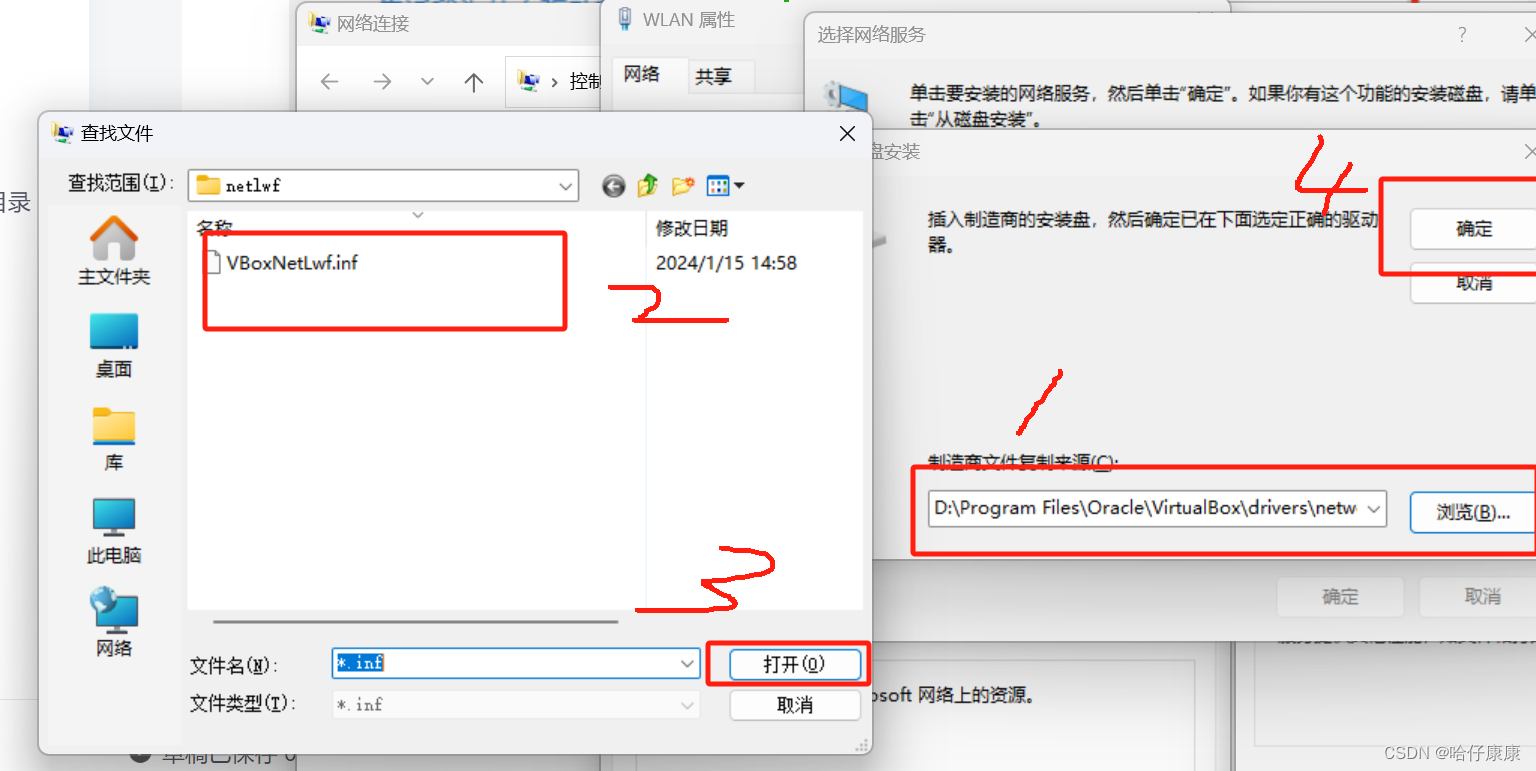
此时出现下面情况就算安装成功
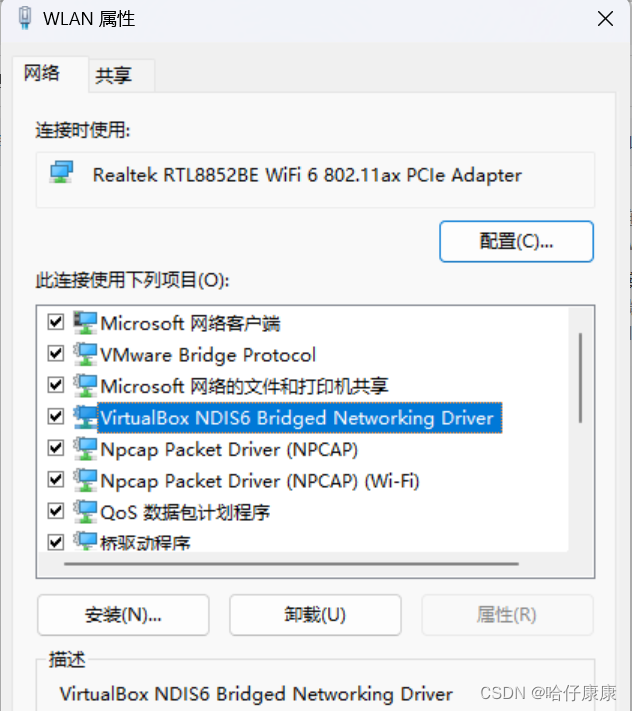
但是如果报错:找不到指定的模块
则按下面步骤删除干净垃圾重新上面操作
先安装CCleaner, 链接:CCleaner Makes Your Computer Faster & More Secure | Official Website
打卡选择
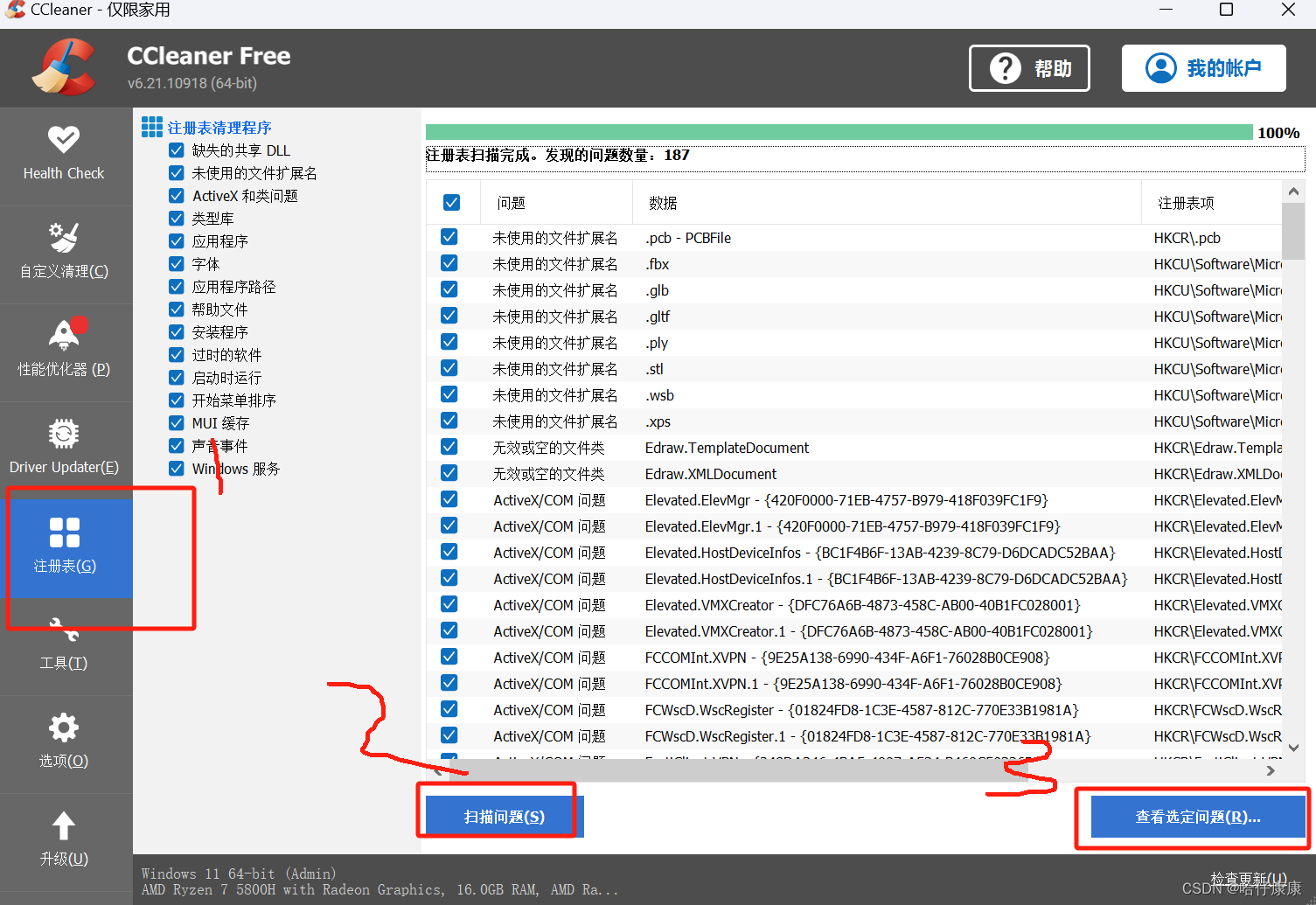
自行选择是或否


此时无用表删除,重新上面安装网卡步骤不再报错,打卡虚拟机,可选择,网络正常
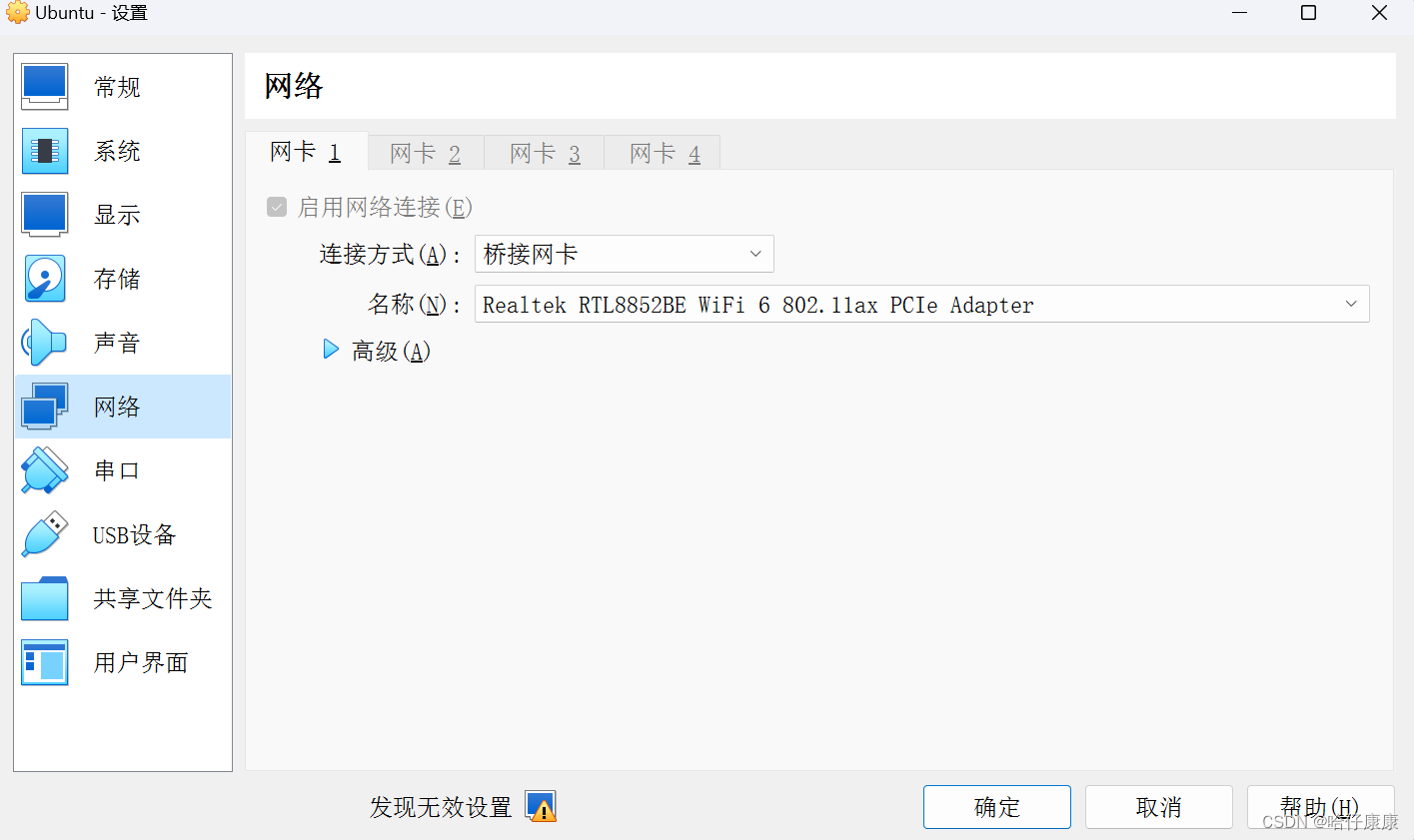
解决办法,安装虚拟网卡,win11查找方式:控制面板→网络和共享中心→更改适配器设置




此时出现下面情况就算安装成功

但是如果报错:找不到指定的模块
则按下面步骤删除干净垃圾重新上面操作
先安装CCleaner, 链接:CCleaner Makes Your Computer Faster & More Secure | Official Website
打卡选择

自行选择是或否


此时无用表删除,重新上面安装网卡步骤不再报错,打卡虚拟机,可选择,网络正常


本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/505786.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!