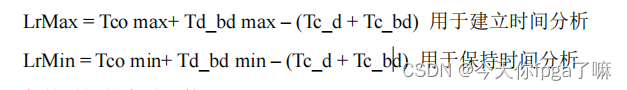前言:前面内容介绍了时序分析的基本原理,着重学习了芯片内部的两级寄存器之间的时序分析模型,本篇内容针对IO部分的时序分析模型展开讨论讲解。
文章目录
- 一、IO接口时序分析的基本模型(源同步)
- 二、INPUT DELAY 时序分析原理
- 建立保持时间余量计算:
- 三、OutPUT DELAY 时序分析原理
- 1.可以知道下游芯片的 setup 门限值
- 1. 建立时间余量计算:
- 2. 保持时间余量计算:
- 2.不知道下游芯片的 setup 门限值,利用skew的思想
- 1. 建立时间余量计算:
- 2. 保持时间余量计算:
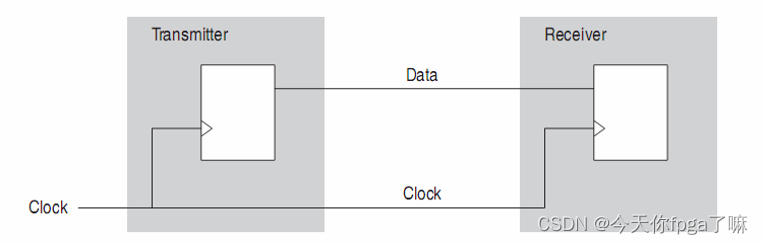
一、IO接口时序分析的基本模型(源同步)
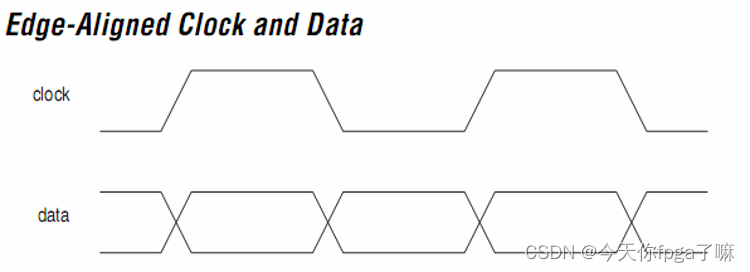
源同步接口是由发送端提供数据和时钟,数据和时钟的对齐方式又有两种:
一种是中心对齐
另外一种是边缘对齐。
如下图所示:
边缘对齐:
中心对齐:
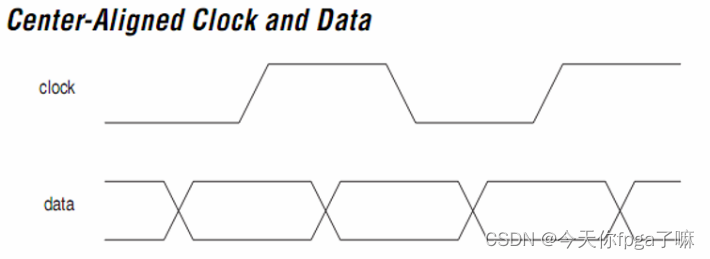
通过源同步中心对齐时序电路推导出广泛适用的输入延迟计算公式
二、INPUT DELAY 时序分析原理
Input delay 需要约束的是发射沿 lunch 沿到数据有效的延迟
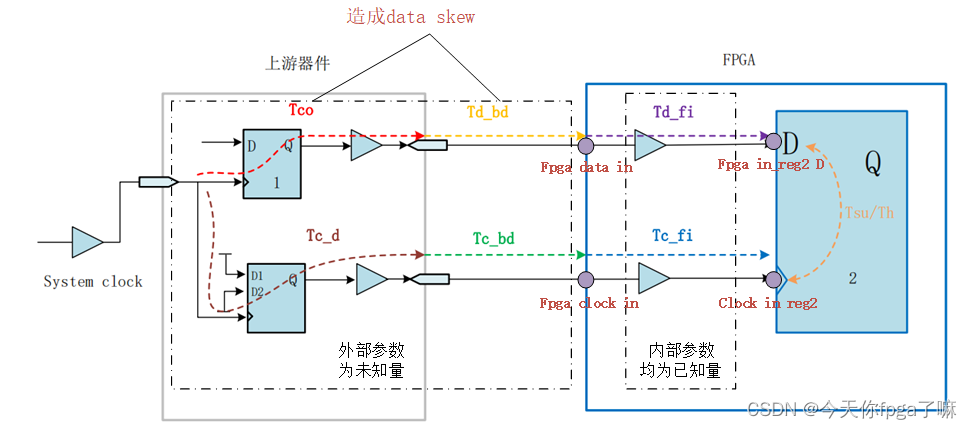
时序图示例建立保持时间余量:
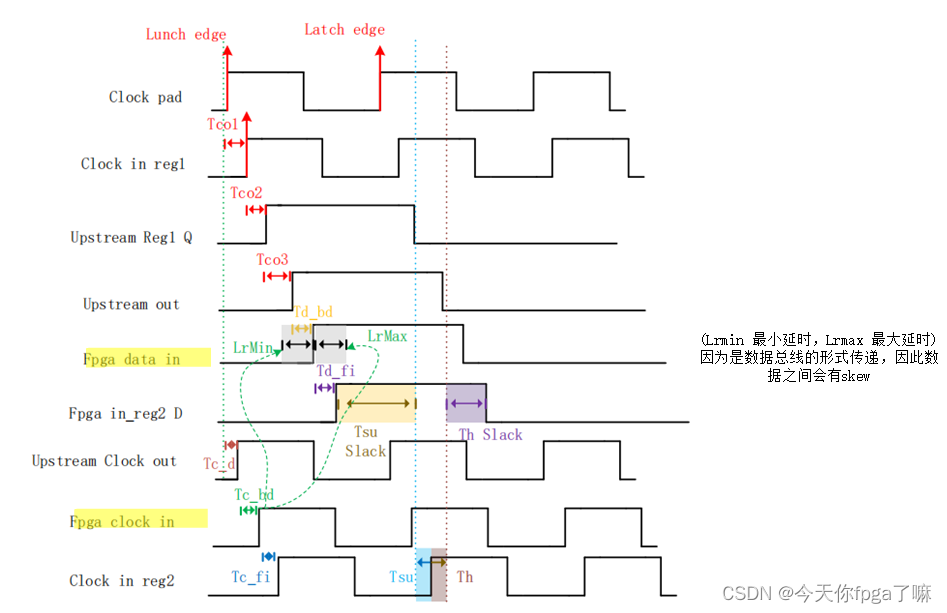
建立保持时间余量计算:
通用计算:
1.建立时间余量计算:
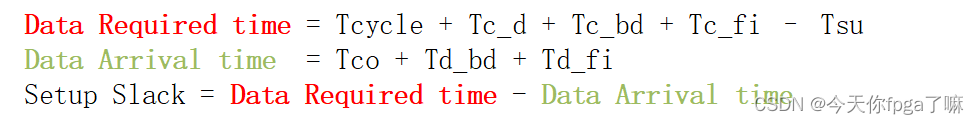
2.保持时间余量通用计算公式:

带入实际模型计算:
1.建立时间余量计算:

2.保持时间余量通用计算公式:

总结:
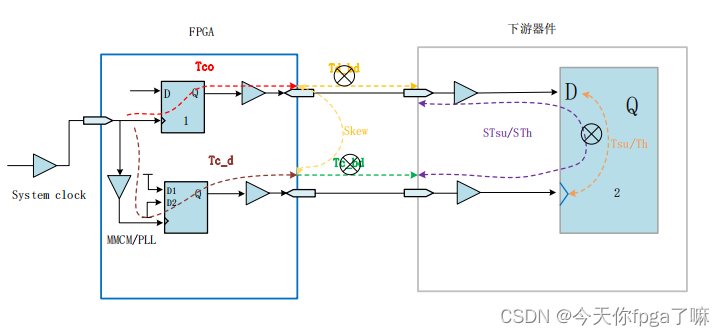
三、OutPUT DELAY 时序分析原理
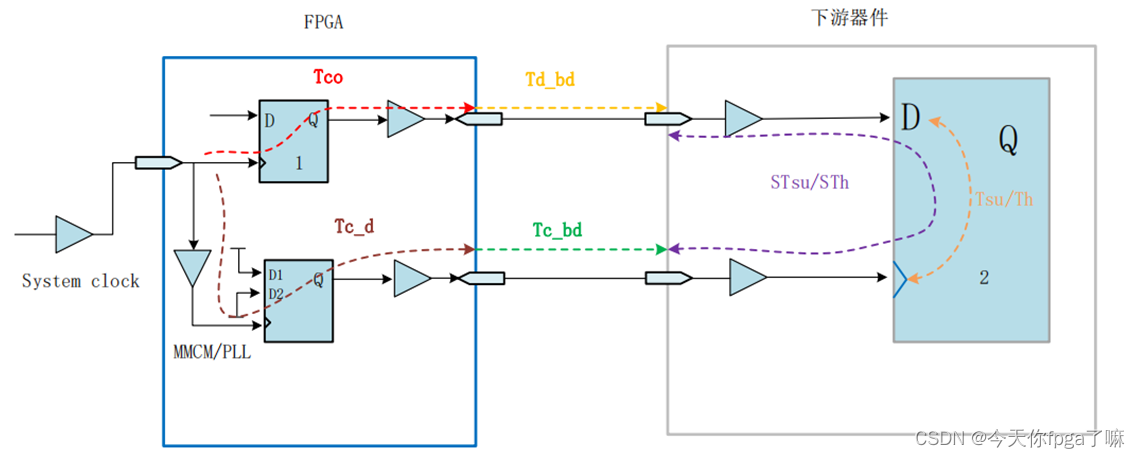
Output delay 时序图
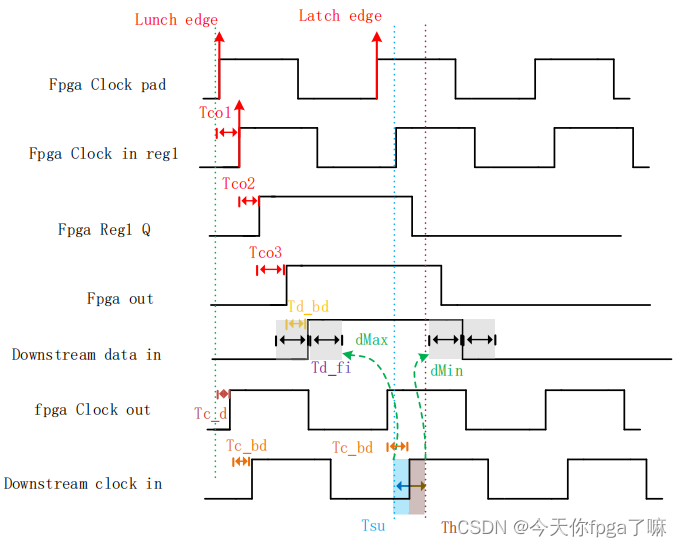
1.可以知道下游芯片的 setup 门限值
1. 建立时间余量计算:
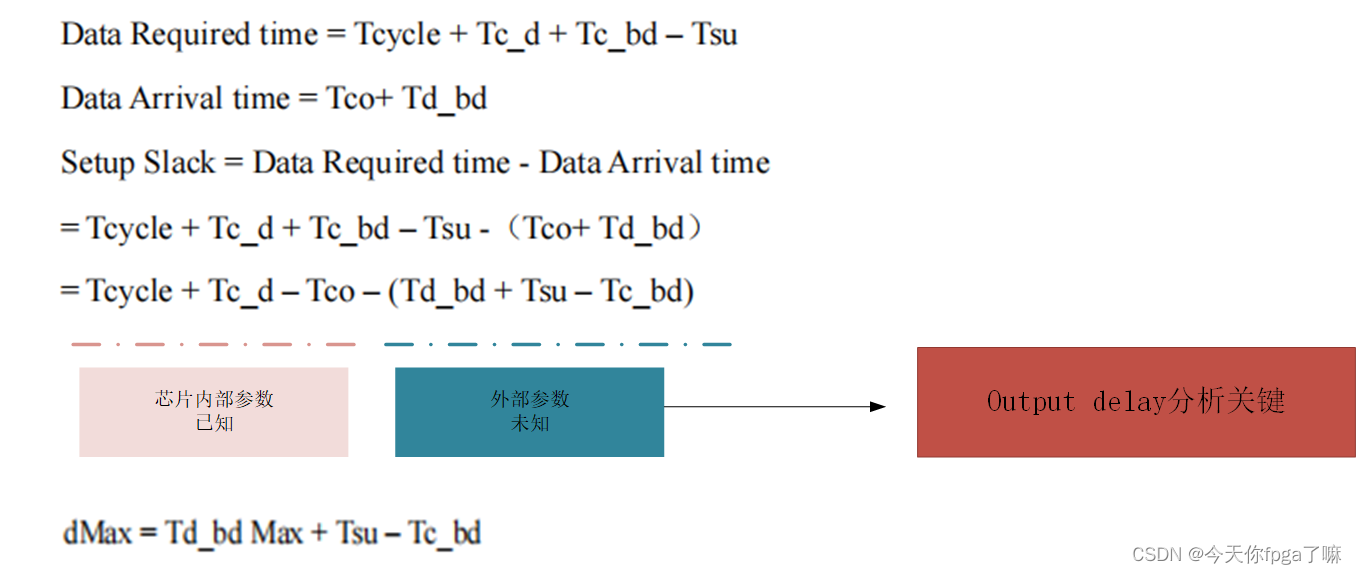
2. 保持时间余量计算:

2.不知道下游芯片的 setup 门限值,利用skew的思想
多数情况下,我们是不知道目标芯片 setup 门限值或者 hold 的门限值怎么办?
答:直接假设输出的时钟与数据的关系,设值为SKEW。假设 SKEW 的目的是让综合工具知道输出的时钟采样沿不能落在 SKEW 的区间,如果落在 SKEW 区间就出现时序违例,这样我们可以假定 SKEW 的大小来调节时钟与数据的关系。
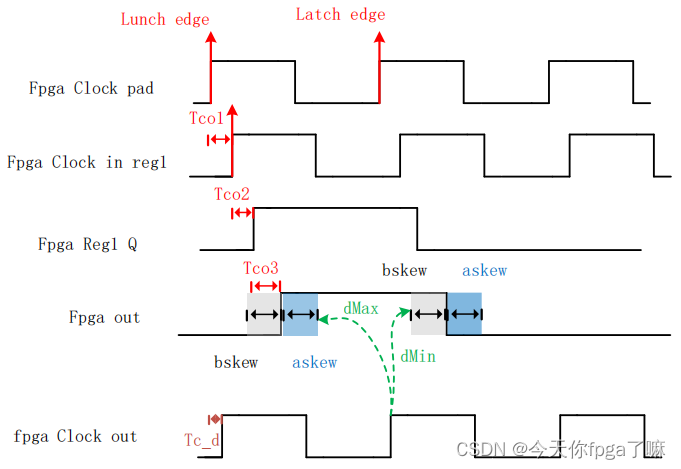
1. 建立时间余量计算:

2. 保持时间余量计算:

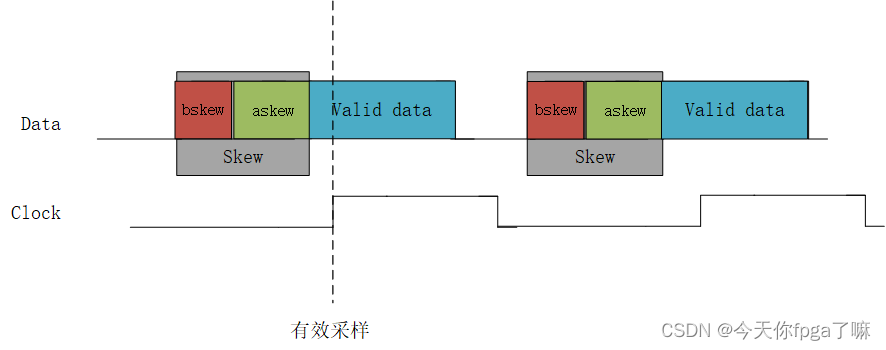
结合上述内容可以看出:合理的设置askew 和 bskew 可以有效避免时序违例的产生